Виды систем эконометрических уравнений. Независимые системы. Рекурсивные системы.

Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования. При использовании отдельных уравнений, регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в последние десятилетия в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений, называемых также структурными уравнениями. Так, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.

Приведем другой пример.

При оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.

В еще большей степени возрастает потребность в использовании системы взаимосвязанных уравнений, если мы переходим от исследований на микроуровне к макроэкономическим расчетам. Модель национальной экономики включает в себя систему уравнений: функции потребления, инвестиций заработной платы, а также тождество доходов и т.д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций.

Система уравнений в эконометрических исследованиях может быть построена по-разному.

Возможна система независимых уравнений, когда каждая зависимая переменная (y) рассматривается как функция одного и того же набора факторов (x) :

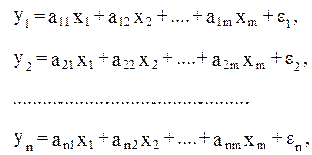
Набор факторов 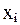в каждом уравнении может варьировать. Так, модель вида

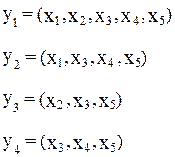
Так же является системой независимых уравнений с тем лишь отличием, что в ней набор факторов видоизменяется в уравнениях, входящих в систему. Отсутствие того или иного фактора в уравнении системы может быть следствием как экономической нецелесообразности его включения в модель, так и несущественности его воздействия на результативный признак (незначимо значение t- критерия или частного F-критерия для данного фактора).

Примером такой модели может служить модель экономической эффективности сельскохозяйственного производства, где в качестве зависимых переменных выступают показатели, характеризующие эффективность сельскохозяйственного производства, продуктивность коров, себестоимость 1 ц молока, а в качестве факторов- специализация хозяйства, количество голов на 100 га пашни, затраты труда и т.п.

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Поскольку никогда нет уверенности, что факторы полностью объясняют зависимые переменные, то в уравнениях присутствует свободный член a_0. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки.

В итоге система независимых уравнений при трех зависимых переменных и четырех факторах примет вид:

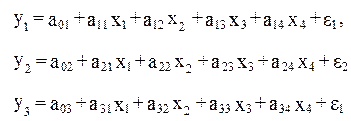
Однако если независимых переменная у донного уравнения выступает в виде фактора x в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:

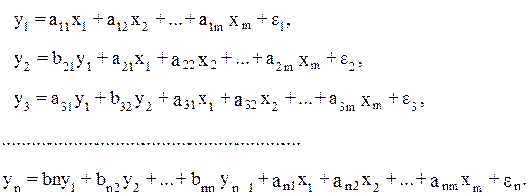
В данной системе зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов x. Примером такой системы может служить модель производительности труда и фондоотдачи вида:

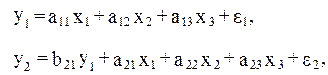
Где y_{1 –} производительность труда;

y₂ – фондоотдача;

x₁ – фондовооруженность труда;

x₂ – энерговооруженность труда;

x₃ – квалификация рабочих.

Как и в предыдущей системе, каждое уравнение может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях- в правую часть системы:

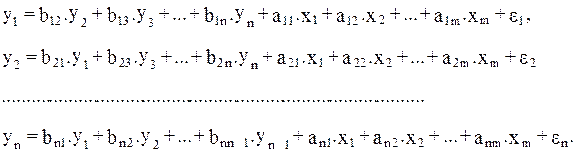
Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные (y) одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостояа уравнений называется также структурной формой модетельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида.

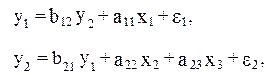
где y₁- темп изменения месячной заработной платы;

y₂ – темп изменения цен;

x₁- процент безработных;

x₂ – темп изменения постоянного капитала;

x₃ – темп изменения цен на импорт сырья.