Система линейных одновременных уравнений. Структурная и приведенная формы эконометрической модели.

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные обозначены в приведенной ранее системе одновременных уравнений как у. Это зависимые переменные, число которых равно числу уравнений в системе.

Экзогенные переменные обозначаются обычно как x. Это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

Простейшая структурная форма модели имеет вид:

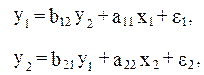
где y – эндогенные переменные;

x – экзогенные переменные.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Так, потребление текущего года (y_t) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (y_t-1)

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты b_i и a_j, (b_i – коэффициент при эндогенной переменной, a_j – коэффициент при экзогенной переменной), которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонения от уровня, т. е. под x подразумевается x- 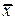а под y - соответственно у- 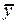. Поэтому свободный член в каждом уравнении системы отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные структурных коэффициентов модели структурная коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

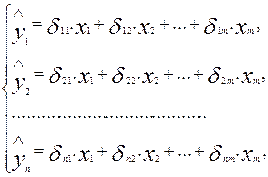
где 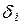- коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели ( ) через коэффициенты структурной модели (a_j и b_i). Для упрощения в модель не введены случайные переменные.

Для структурной модели вида

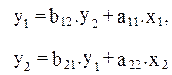и (4.1)

Приведенная форма модели имеет вид

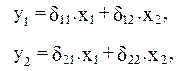и (4.2)

В которой y₂ из первого уравнения структурной модели можно выразить следующим образом:

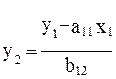
Тогда система одновременных будет представлена как

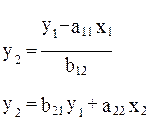
Отсюда имеем равенство:

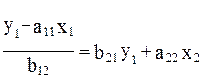
Или

Тогда

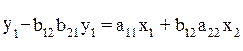
Или

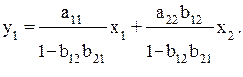
Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:

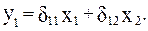
Из уравнения следует, что коэффициенты приведенной формы модели представляют собой нелинейные соотношения коэффициентов структурной модели, т. е.

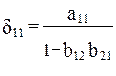и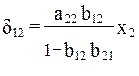

Аналогично находятся и коэффициенты приведенной формы модели второго уравнения системы ( 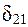и 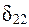) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную 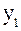из второго структурного уравнения и подставим во второе.

Что соответствует уравнению приведенной формы модели:

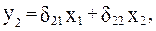
т.е.

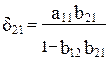и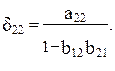

Эконометрические модели обычно включают в систему не только уравнения, отражающие взаимосвязи еменную им турнвязаны с коэффодели второго уравнения системы ()дели в виде уравнения приведенной формы модели:

между отдельными переменными, но и выражения тенденции развития явления, а также разного рода тождества. Так, в 1947 г., исследуя линейную зависимость потребления (c) от дохода (y), Т. Хавельмо предложил одновременно учитывать тождество дохода. В этом случае модель имеет вид:

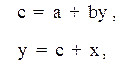
где х – инвестиции в основной капитал и запасы экспорта и импорта;

a и b – параметры линейной зависимости c от y.

Их оценки должны учитывать тождество дохода в отличие от параметров обычной линейной регрессии.

В этой модели две эндогенные переменные – c и y и одна экзогенная переменная x. Система приведенных приведенных уравнений составит:

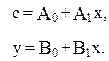
Она позволяется получить значения эндогенной переменной с через переменную х. Рассчитав коэффициенты приведенной формы модели (A₀, A₁, B₀, B₁), можно перейти к коэффициентам структурной модели a и b, подставляя в первое уравнение приведенной формы выражение переменной x из второго уравнения приведенной формы модели. Приведенная форма модели хотя и значения экзогенных переменных, аналитически уступает структурной форме модели, так в ней отсутствуют оценки взаимосвязи между эндогенными переменными.