Уравнение регрессии с фиктивными переменными для временного ряда потребления электроэнергии
| переменная | коэффициент | стандартная ошибка | т- критерий |
| константа | 8,3250 | 0,227261 | 36,6318 |
| t | 0,1875 | 0,016939 | 11,0691 |
| х1 | -2,0875 | 0,220208 | -9,4797 |
| х2 | -4,4750 | 0,216926 | -20,6292 |
| х3 | -3,9125 | 0,214933 | -18,2034 |
| R2 = 0.985 |
Проанализируем эти результаты. Влияние сезонной компоненты в каждом квартале статистически значимо (фактические значения т-критерия по модулю больше 2 для параметров при переменных х1, х2, х3 и константа а). Параметр а =8,33 есть сумма начального уровня ряда и сезонной компоненты в 4-ом квартале.
Сезонные колебания в I, II, III кварталах приводят к снижению этой величины, о чем свидетельствуют отрицательные оценки параметров при переменных х1, х2, х3. Отметим, что эти параметры не равны значениям сезонной компоненты, поскольку они характеризуют не сезонного изменения от уровней, учитывающих сезонные воздействия в 4-ом квартале. Положительная величина параметра b =0.19 при переменной времени свидетельствует о наличии возрастающей тенденции в уровнях ряда. Его абсолютное значение говорит о том, что средний за квартал абсолютный прирост объема потребления электроэнергии составляет 0,19 млн кВт.ч, или 190 тыс. кВт.ч. Поскольку фактическое значение т-критерия Стьюдента равно 11.1, можно утверждать, что существование в уровнях ряда тенденции установлено надежно.
Коэффициент детерминации в данной модели R2 = 0.985. Общая сумма квадратов уровней ряда Yt составляет:
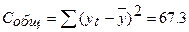
Определим остаточную сумму квадратов.
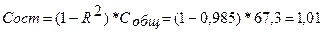
Остаточная сумма квадратов по аддитивной модели (сумма квадратов абсолютных ошибок) была рассчитана ранее (табл.5.10) и составляет 1.1. Следовательно, модель регрессии с фиктивными переменными описывает динамику временного ряда потребления электроэнергии лучше, чем аддитивная модель.
Основной недостаток модели с фиктивными переменными для описания сезонных и циклических колебаний – наличие большого количества переменных. Если, пример, строить модели для описания помесячных периодических колебаний за несколько лет, таким образом такая модель будет включать 12 независимых переменных (11 фиктивных переменных и фактор времени). В такой ситуации число степеней свободы невелико, что снижает вероятность получения статистически значимых оценок параметров уравнения регрессии.
Особенности изучения взаимосвязанных временных рядов. Автокорреляция рядов динамики и методы ее устранения. Метод последовательных разностей. Интерпретация параметров уравнения регрессии, построенного оп первым и вторым разностям. Метод отклонения уровней ряда от основной тенденции. Метод включения фактора времени.
От сезонных и циклических колебаний следует отличать единовременные изменения характера тенденции временного ряда, вызванные структурными изменениями в экономике или иными факторами. В этом случае, начиная с некоторого момента времени t, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику. Схематично такая ситуация изображена на рис. 5.8.
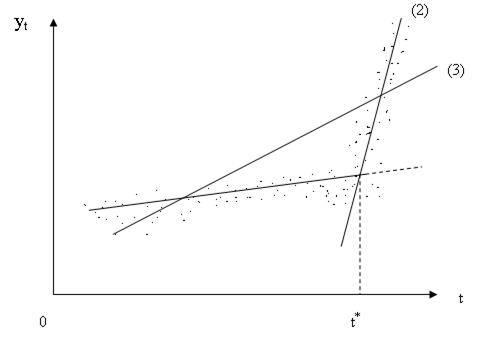
Рис 5.8. Изменение характера тенденции временного ряда
* Интерпретация параметров уравнения регрессии, построенного по первым и вторым разностям. Метод отклонения уровней ряда от основной тенденции. Метод включения фактора времени.
Момент (период) времени t* сопровождается значительными изменениями ряда факторов, оказывающих сильное воздействие на изучаемый показатель уt. Чаще всего эти изменения вызваны изменениями в общеэкономической ситуации или факторами (событиями) глобального характера, приведшими к изменению структуры экономики (например, начало крупных экономических реформ, изменение экономического курса, нефтяные кризисы и другие факторы). Если исследуемый временной ряд включает в себя соответствующий момент (период) времени, то одной из задач его изучения становится выяснение вопроса о том, значимо ли повлияли общие структурные изменения на характер этой тенденции.
Если это влияние значимо, то для моделирования тенденции данного временного ряда следует использовать кусочно-линейные модели регрессии, т.е. разделить исходную совокупность на две подсовокупности (до момента времени t* и после момента t*) и построить отдельно по каждой совокупности уравнения линейной регрессии (на рис. 5.8. этим уравнениям соответствуют прямые (1) и (2)). Если структурные изменения не значительно повлияли на характер тенденции ряда yt, то ее можно описать с помощью единого для всей совокупности данных уравнения тренда (на рис. 5.8. этому уравнению соответствует прямая (3)).
Каждый из выписанных выше подходов имеет свои положительные и отрицательные стороны. При построении кусочно-линейной модели происходит снижение остаточной суммы квадратов по сравнению с единым для всей совокупности уравнением тренда. Однако разделение исходной совокупности на две части ведет к потере числа наблюдений и, следовательно, к снижению числа степеней свободы в каждом уравнении кусочно-линейной модели. Построение единого для всей совокупности уравнения тренда, напротив, позволяет сохранить число наблюдений n исходной совокупности, однако остаточная сумма квадратов по этому уравнению будет выше по сравнению с кусочно-линейной моделью. Очевидно, что выбор одной из двух моделей (кусочно-линейной или единого уравнения тренда) будет зависеть от соотношения между снижением остаточной дисперсии и потерей числа степеней свободы при переходе от единого уравнения регрессии к кусочно-линейной модели.
Таблица 5.17
Условные обозначения для алгоритма теста Чоу
| № уравнения | Вид уравнения | Число наблюдений в совокупности | Остаточная сумма квадратов | Число параметров в уравнении1 | Число степеней свободы остаточной дисперсии |
| Кусочно-линейная модель | |||||
| (1) | y(1)=а1+b1t | n1 | C1ост | k1 | n1- k1 |
| (2) | y(2)=а2+b2t | n2 | C2ост | k2 | n2- k2 |
| Уравнение тренда по всей совокупности | |||||
| (3) | y(3)=а3+b3t | n | C3ост | k3 | n-k3=(n1+n2)-k3 |
| 1В рассматриваемой нами формулировке число параметров всех уравнений k1= k2= k3=2. В общем случае число параметров в каждом уравнении может различаться. |
Формальный статистический тест для оценки этого соотношения был предложен Грегори Чоу. Применение этого теста предполагает расчет параметров уравнений трендов. Графики которых изображены на рис. 5.8 прямыми (1), (2) и (3). Введем систему обозначений, приведенную в табл. 5.17.
Выдвинем гипотезу Но о структурной стабильности тенденции изучаемого временного ряда.
Остаточную сумму квадратов по кусочно-линейной модели (Склост) можно найти как сумму C1ост и C2ост:
Cклост= C1ост+ C2ост. (5.18)
Соответствующее ей число степеней свободы составит:
(n1 – k1) + (n2 – k2) = (n – k1 – k2) (5.19)
Тогда сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочно-линейной модели можно определить следующим образом:
DCост= C3ост+ Cклост. (5.20)
Число степеней свободы, соответствующее DCост, с учетом соотношения (5.19) будет равно:
n – k3 – (n – k1 – k2) = k1 +k2 – k3. (5.21)
Далее в соответствии с предложенной Г. Чоу методикой определяется фактическое значение F-критерия по следующим дисперсиям на одну степень свободы варияции:
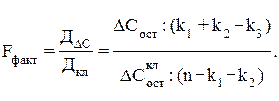 (5.22)
(5.22)
Найденное значение Fфакт сравнивают с табличным, полученным по таблицам распределения Фишера для уровня значимость a и числа степеней свободы ( k1 +k2 – k3) и (n – k1 – k2).
Если Fфакт > Fтабл, то гипотеза о структурной стабильности тенденции отклоняется, а влияние структурных изменений на динамику изучаемого показателя признают значимым. В этом случае моделирование тенденции временного ряда следует осуществлять с помощью кусочно-линейной модели. Если Fфакт < Fтабл, то нет оснований отклонять ноль-гипотезу о структурной стабильности тенденции. Ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения тренда.
Отметим следующие особенности применения теста Чоу:
1. Если число параметров во всех уравнениях (1), (2) и (3) (см. рис. 5.8 и табл. 5.17) одинаково и равно k, то формула (5.12) упрощается:
 (5.23)
(5.23)
2. Тест Чоу позволяет сделать вывод о наличии или остутствии структурной стабильности в изучаемом временном ряде. Если Fфакт < Fтабл, то означает, что уравнения (1) и (2) описывают одну и ту же тенденцию, а различия численных оценок их параметров а1 и а2, а также b1 и b2 соответственно статистически не значимы. Если Fфакт > Fтабл, то гипотеза о структурной стабильности отклоняется, что означает статистическую значимость различий оценок параметров уравнений (1) и (2).
3. Применение теста Чоу предполагает соблюдение предпосылок о нормальном распределении остатков в уравнениях (1) и (2) и незначимость их распределений.
Если гипотеза о структурной стабильности тенденции ряда уt отклоняется, дальнейший анализ может заключаться в исследовании вопроса о причинах этих структурных различий и более детальном изучении характера изменения тенденции. В принятых нами обозначениях эти причины обуславливают различия оценок параметров уравнений (1) и (2).
Возможны следующие сочетания изменения численных оценок параметров этих уравнений (рис 5.9):
· изменение численной оценки свободного члена уравнения тренда а2 по сравнению а1 при условии, что различия между b1 и b2 статистически незначимы. Геометрически это означает, что прямые (1) и (2) параллельны (рис 5.9 а). В данной ситуации можно говорить о скачкообразном изменения уровней уt в момент времени t* при неизменном среднем абсолютном приросте за период;
· изменение численной оценки параметра b2 по сравнению с b1 при условии, что различия между а1 и а2 статистически незначимы. Геометрически это означает, что прямые (1) и (2) пересекают ось ординат в одной точке (рис 5.9 б). В этом случае изменение тенденции связано с изменением среднего абсолютного прироста временного ряда, начиная с момента времени t*, при неизменном начальном уровне ряда в момент времени t = 0;
· изменение численных оценок параметров а1 и а2, а также b1 и b2. Геометрически эта ситуация изображена на рис. 5.9 в. Она означает, что изменение характера тенденции сопровождается изменением как начального уровня ряда, так и среднего за период абсолютного прироста.
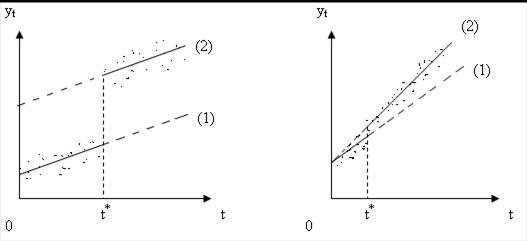
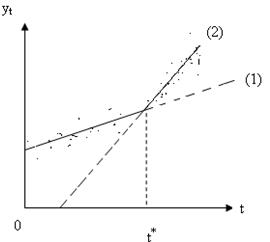
Рис. 5.9. Изменение тенденции временного ряда при различном сочетании статистической значимости изменений параметров а1 и а2; b1 и b2;
а - статистически значимым является различие только между а1 и а2;
б - статистически значимым является различие только между b1 и b2;
в - статистически значимым является различие между а1 и а2,
а также между b1 и b2;
Один из статистических методов тестирования при применении перечисленных выше ситуации характеристики тенденции изучаемого временного ряда был предложен американским экономистом Дамодаром Гуйарати. Этот метод основан на включении в модель регрессии фиктивной переменной Zt, которая принимает значения 1 для всех t < t*, принадлежащие промежутку времени до изменения характера тенденции, далее промежутку (1), и 0 значения для всех t > t*, принадлежащие промежутку времени после изменения характера тенденции, далее промежутку (2). Д. Гуйарати предполагает определять параметры следующего уравнения регрессии:
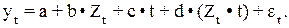 (5.24)
(5.24)
Таким образом, для каждого промежутка времени получим следующие уравнения:
Промежуток (1) Z = 1 
Промежуток (2) Z = 0 
Сопоставив полученные уравнения с уравнениями (1) и (2), нетрудно заметить, что
а1 = (а + b); b1 = (c + d); (5.25)
a2 = a; b2 = c.
Параметр b есть разница между свободными членами уравнений (1) и (2), а параметр d - разница между параметрами b1 и b2 уравнений (1) и (2). Оценка статистической значимости различий а1 и а2, а также b1 и b2 эквивалентна оценке статистической значимости параметров b и d уравнения (5.24). Эту оценку можно провести при помощи t-критерия Стьюдента.
Таким образом, если в уравнении (5.24) b является статистически значимым, а d – нет, то изменение тенденции вызвано только различиями параметров а1 и а2 (рис. 5.9 а). Если в этом уравнении параметр d – статистически значим, а b – незначим, то изменение характера тенденции вызвано различиями параметров b1 и b2 (рис. 5.9. б). Наконец, если оба коэффициента b и d являются статистически значимыми, то на изменение характера тенденции повлияли как различия между а1 и а2, так и различия между b1 и b2 (рис. 5.9.в).
Этот метод можно использовать не только в дополнение к тесту Чоу, но и самостоятельно для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда. Основное его преимущество перед тестом Чоу состоит в том, что нужно построить только одно, а не три уравнения тренда.
Мы рассмотрели простейший случай применения теста Чоу для моделирования линейной тенденции. Однако этот тест (а также модель (5.24) с фиктивной переменной) может использовать (и действительно используется во многих прикладных исследованиях) при проверке гипотез о структурной стабильности и в более сложных моделях взаимосвязи двух и более временных рядов.
Дата добавления: 2016-05-16; просмотров: 1213;
