Применение систем эконометрических уравнений
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большего числа факторов, влияющих на экономические переменные, исследователь, как правило, неуверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о моделируемом объекте, которое сложность на данный момент и может изменяться. Соответственно может изменяться и вид модели с точки зрения ее идентифицируемости.
Сверхидентифицируемую модель можно превратить в точно идентифицируемую путем добавления некоторых переменных или отбрасывания некоторых ограничений на параметры. Не исключено, что при правильной спецификации модели она может оказаться неидентифицируемой, и поэтому переходят к сверхидентифицируемым моделям, несколько упрощающим характер взаимосвязей экономических явлений. Отметим, что наличие множества прикладных моделей для решения одного и того же класса задач не случайно. Наиболее ярко это проявляется при построении макроэкономических моделей, когда, например, она и та же функция потребления может включать в себя разный набор экономических переменных.
Рассмотрим основные направления практического использования эконометрических систем уравнений.
Наиболее широко системы одновременных уравнений используются для построения макроэкономических моделей функционирования экономики той или иной страны. Большинство из них представляют собой мультипликаторные модели кейнсианского типа с той или иной сложности. Статическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте имеет следующий вид:
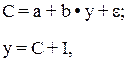
где С – личное потребление в постоянных ценах;
у – национальный доход в постоянных ценах;
I – инвестиции в постоянных ценах;
e – случайная составляющая.
В силу наличия тождества в модели (второе уравнение системы) структурный коэффициент b не может быть больше 1. он характеризует придельную склонность к потреблению. Так если b = 0,65, то из каждой дополнительной тысячи дохода на потребление расходуется в среднем 650 руб. и 350 руб. инвестируется, т.е. С и у выражены в тыс. руб. Если b>1, то y<C+I, т.е. на потребление расходуются не только доходы, но и сбережения. Параметр а Кейнс истолковывал как прирос потребления за счет других факторов. Так как прирост по времени может быть не только положительнымнвестируется, т.е. немлениблению. фициент й вид:
ныта же функция потребления может включатьвремени)., но и отрицательным (снижение), то такой вывод возможен. Однако служение о том, что параметр а характеризует конкретный уровень потребления, обусловленный влиянием других факторов, неправильно.
Структурный коэффициент b используются для расчета мультипликаторов. По данной функции потребления можно определить два мультипликатора – инвестиционный мультипликатор потребления Мс инвестиционный мультипликатор национального дохода Му.
Инвестиционный мультипликатор потребления определяется по формуле
Мс = b / (1 - b).
При b = 0,65 Mc = 0,65 / (1 – 0,65) = 1,857.
Эта величина означает, что дополнительные вложения в размере 1 тыс. руб. приведут при прочих равных условиях к дополнительному увеличению потребления на 1,857 тыс. руб.
Инвестиционный мультипликатор национального дохода можно определять как Му = b / (1 - b). В нашем случае он составит:
Му = 1 / (1 – 0,675) = 2,857,
т.е. дополнительные инвестиции в размере 1 тыс. руб. на длительный срок приведут при прочих равных условиях к дополнительному доходу в 2,857 тыс. руб.
Рассматриваемая модель Кейнса точно идентифицируема, и для получения величины структурного коэффициента b применяется КМНК. Это значит, что строится система приведенных уравнений:
С = А + В I + U1’,
у = А’ + В’ I + U1,
в которой А = А’, а параметры В и B’ являются мультипликаторами, т.е. у=Мс и B’=Му. Убедиться в этом можно, если выразить коэффициенты приведенной формы модели через структурные коэффициенты. Для этого в первое уравнение структурной модели поставим балансовое равенство:
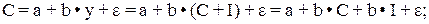
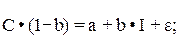
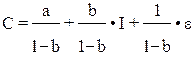- приведенное уравнение.
Отсюда А = a /(1 – b); B = b / (1 – b) = MC; U1 = (1 / (1 – b))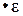 
.
Аналогично поступим и со вторым уравнением структурной модели: в тождество у = С + I вместо С поставим выражение первого структурного уравнения, т.е.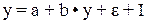 
. Далее преобразовывая, получим:
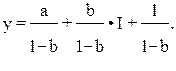
т.е. А’ = a /(1 – b) = A; B’ = b / (1 – b) = My; U2 = (1 / (1 – b)) .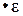
Таким образом, приведенная форма модели содержит мультипликаторы, интерпретируемые как коэффициенты линейной регрессии, отвечающие на вопрос, на сколько единиц изменится значение эндогенной переменной, если экзогенная переменная изменится на 1 ед. своего измерение. Этот смысл коэффициентов приведенной формы делает приведенную модель удобной для прогнозирования.
В более поздних исследованиях статистическая модель Кейнса включала уже не только функцию потребления, но и функцию сбережений:
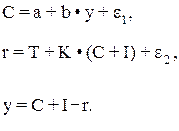
где С, у и I – те же по смыслу переменные, что в предыдущей модели;
r - сбережения.
Данная модель содержит три эндогенные переменные – С, r, у и одну экзогенную переменную I. Система идентифицируема: в первом уравнении Н=2 и D=1, во втором Н=1 и D=0; С+I рассматривается как предопределенное переменное (подобное изложение решения данной системой приведено в работе Г. Тингнера). Наряду со статистическими широкое распространение получил динамические модели экономики. В отличие от статических они содержат в правой части лаговые переменные, а также учитывают тенденции (фактор времени). Примером могут служить модели Л. Клейна, разработанные им для Экономики США в 1950-1960 гг. В упрошенном варианте модель Клейна рассматривается как конъюнктурная модель.
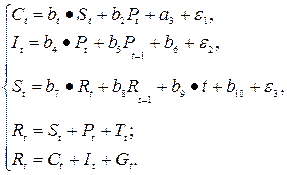
где Сt – функция потребления в период t;
St – заработная плата в период t;
Pt – прибыль в период t;
Pt-1 – прибыль в период t – 1, т.е. в предыдущий год;
Rt – общий доход в период t;
Rt-1 – общий доход в предыдущий период;
t – время
Tt – чистые трансферты в пользу администрации в период t;
It – капиталовложения в период t;
Gt – спрос административного аппарата, правительственные расходы в период времени t.
Модель содержит пять эндогенных переменных - Сt, It, St, Rt (расположены в левой части системы) и Rt (последняя – зависимая переменная, определяемая по первому тождеству), три экзогенных переменных - Tt, Gt, t и две предопределенные, лаговые переменные - Pt-1 и Rt-1. Как и большинство моделей такого типа, данная модель сверхидентифицируема и решаема ДМНК. Для прогнозных целей используется приведенная форма модели:
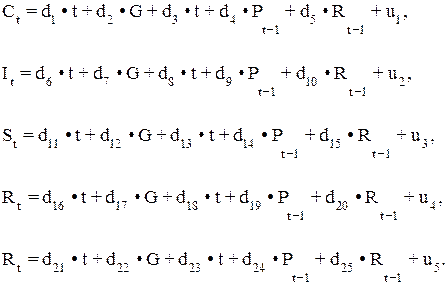
В данной системе мультипликаторами являются коэффициенты для обычных экзогенных переменных. Они отражают влияние экзогенной переменной на эндогенную переменную. Мультипликаторами в нашем примере выступают коэффициенты при T и G. Коэффициенты d1, d6, d11, d16, d21, - мультипликаторы чистых трансфертов в пользу администрации относительно личного потребления d1, инвестиции d6, заработной платы d11, дохода d16 и прибыли d21, соответственно коэффициенты d2, d7, d12, d17, d22 являются мультипликаторами правительственных расходов относительно соответствующих эндогенных переменных.
Динамическая модель может и не содержать учет тенденции, но лаговые переменные в ней обязательны. Динамическая модель Кейнса представлена следующими тремя уравнениями:
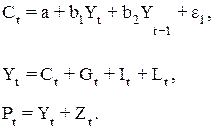
В этой системе три эндогенные переменные:
Уt – имеющейся в распоряжении доход в период времени t;
Ct – частное потребление в период времени t;
Pt – валовой национальный продукт (ВНП) в период времени t;
Кроме того, модель содержит пять преопределенных переменных:
Yt-1 – доход предыдущего года;
Gt – общественное потребление;
It – валовые капиталовложения;
Lt – изменение складских запасов;
Zt – сальдо платежного баланса.
Случая переменная e1 характеризует ошибки в первом уравнении в виду его статистического характера. Параметр а отражает влияние других не учитываемых в данном уравнении факторов потребления (например, цен). Первое уравнение данной системы является сверхидентифицируемым, а второе и третье – определениями.
Если в модель Кейнса доход рассматривается лаговая переменная, то в других исследованиях функции потребления в виде лаговой переменной используются потребление предыдущего года, т.е. считается, что потребление текущего года зависит не только от дохода, но от достигнутого в предыдущий период уровня потребления.
Примером динамической модели экономики, учитывающей для каждой эндогенной переменной лаговые переменные соответствующего экономического содержания, может служить модель открытой экономики с экономической активностью со стороны государства.
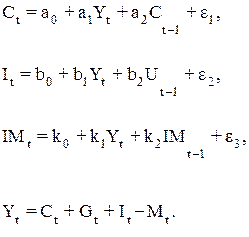
В этой системе четыре эндогенных переменных:
Ct – личное потребление в период времени t;
It – частные чистые инвестиции в отрасли экономики в период времени t;
IMt – импорт в период времени t;
Уt – национальный доход за период времени t.
Все переменные приведены в постоянных ценах.
Преопределенными переменными в модели являются следующие три переменные:
Ct-1 – личное потребление за предыдущий период;
Ut-1 – доход личных домохозяйств от предпринимательской деятельности за предыдущий период и доход от имущества плюс нераспределенная прибыль предприятия до налогообложения;
IMt-1 – импорт за предыдущий период времени t - 1.
В качестве экзогенной переменной в модели рассматривается переменная Gt – общественное потребление, плюс государственные чистые капиталовложения в экономику страны, плюс изменение запасов, минус косвенные налоги, плюс дотации, плюс экспорт.
Первые три уравнения системы являются сверхидентифицируемыми, а четвертое представляет собой балансовое тождество.
Система одновременных уравнений нашла применение в исследованиях спроса и предложения. Линейная модель спроса и предложения имеет вид:
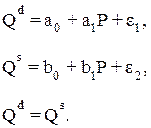
где Qd – спрашиваемое количество благ (объем спроса);
Qs – предлагаемое количество благ (объем предложения);
P – цена.
В этой системе три эндогенные переменные - Qd, Qs и Р. При этом если Qd и Qs представляют собой эндогенные переменные исходя из самой системы (они расположены в левой части) то Р является эндогенной по экономическому содержанию (цена зависит от предлагаемого и спрашиваемого количества благ, а также в результате наличия тождества Qd=Qs.
Приравняв первое и второе уравнения, можно показать, что Р – зависимая переменная:
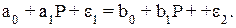
Отсюда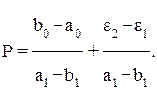 
Рассматриваемая модель спроса и предложения не содержит экзогенной переменной. Однако чтобы модель имела статистическое решение и можно было убедиться в ее справедливости, в модель вводятся экзогенные переменные.
Одним из вариантов модели спроса и предложения является модель вида:
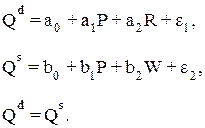
где R – доход на душу населения;
W – климатические условия (предположим, что речь идет о спросе и предложении зерна).
Переменные R и W экзогенные. Введя их в модель, получим идентифицируемую структурную модель, оценки параметров которой могут быть даны с помощью МНК.
Широкий класс моделей в эконометрике представляют производственные функции – Р = f(x1, x2,… xn), где Р – объем выпуска (уровень производства); x1, x2,… xn – факторы производства (труд, капитал, и др.). Однако реализации такого рода моделей, как правило, не связана с системой одновременных уравнений. Производственная функции в упрощенном виде может быть включена в систему одновременных уравнений. Так в 1962 г. Б. Хохалме и Г.Тинтнер предложили следующую модель экономики для каждой из одиннадцати стран – членов ОЭС:
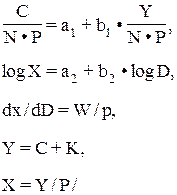
Здесь эндогенными переменными является:
С – величина личного потребления в текущих ценах;
У – ВНП в текущих ценах;
Х – ВНП в постоянных ценах;
Р – индекс цен;
D – общая занятость.
В качестве экзогенных переменных приняты:
N – численность населения;
W – средняя годовая заработная плата работника;
K – государственное потребление плюс инвестиции и внешнеторговое сальдо.
В системе имеются только два структурных уравнения – функция потребления (первое уравнение) и производственная функция (второе уравнение). Остальные составляющие модели представляют собой априорно разработанную функцию спроса на труд (третье уравнение) и два тождества, относящиеся к ВНП.
Параметры функции потребления оцениваются с помощью КМНК с учетом тождества У = С + К, а параметры производственной функции – при комбинации ее с функцией спроса на труд.
[1] моделирование циклических колебаний в целом осуществляется аналогично моделированию сезонных колебаний, поэтому мы рассмотрим только методы моделирования последних.
Дата добавления: 2016-05-16; просмотров: 1035;