Для временного ряда расходов на конечное потребление, д.е.

t	yt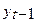
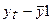
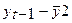
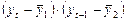
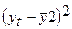
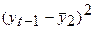
1 7 - - - - - - 2 8 7 -3,29 -3 9,87 10,8241 9 3 8 8 -3,29 -2 6,58 10,8241 4 4 10 8 -1,29 -2 2,58 1,6641 4 5 11 10 - 0,29 0 0 0,0841 0 6 12 11 0,71 1 0,71 0,5041 1 7 14 12 2,71 2 5,42 7,3441 4 8 16 14 4,71 4 18,84 22,1841 16 Σ 86 70 - 0,03* 0 44 53,4287 38 * сумма не равна 0 ввиду наличия ошибок округления

Разумно предложить, что расходов на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет.

Определим коэффициент корреляции между рядами 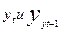и измерим тесноту связи между расходами на конечное потребление текущего и предыдущего годов. Добавим в табл. 5.1 временной ряд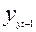

Одна из рабочих формул для расчета коэффициента корреляции имеет вид:

.

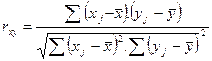В качестве переменной x мы рассмотрим ряд y­₂,y₃,…,y_8; в качестве переменной y – ряд y₁,y₂,…,y₇. Тогда приведенная выше формула примет вид

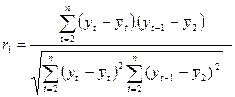(5.1)

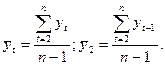Где (5.2)

Эту величину называют коэффициентом автокорреляции уровней ряда порядка, так как он измеряет зависимость между соседними уровнями ряда t и t-1, т.е. при лаге 1.

Для данных примера 5.1 соотношения (5.2) составят:

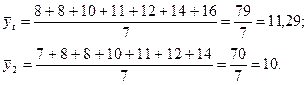
Используя формулу (5.1), получаем коэффициент автокорреляции первого порядка:

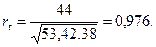
Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующего годов и, следовательно, о наличии во временном ряде расходов на конечное потребление сильной линейной тенденции.

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями 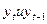и определяется по формуле

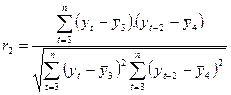(5.3)

где 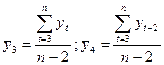. (5.4)

Для данных из примера 5.1 получим:

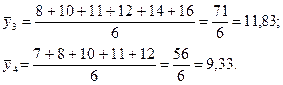
Построим табл.5.2.

Подставив полученные значения в формулу (5.3), имеем:

.

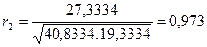Таблица 5.2