Модели стационарных и нестационарных временных рядов и их идентификация.
Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Стационарные временные ряды применяются, в частности, при описании случайных составляющих анализируемых рядов.
Временной ряд yt (t= 1,2,…,n) называется строго стационарным ( или стационарным в узком смысле ), если совместное распределение вероятностей n наблюдений y1,y2,…..,yn такое же, как и n наблюдений y1+t,y2+t,....yn+t при любых n, t и t. Другими словами, свойства строго стационарных рядов yt не зависит от момента t, т.е. закон распределения и его числовые характеристики не зависят от t. Следовательно, математическое ожидание ay(t) = a, среднее квадратическое отклонение sу(t) = s могут быть оценены по наблюдениям yt (t= 1,2,…,n) по формулам:
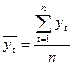 (6.2)
(6.2)
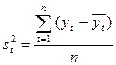 (6.3)
(6.3)
Простейшим примером стационарного временного ряда, у которого математическое ожидание равно нулю, а ошибок et некоррелированы, является «белый шум». Следовательно, можно сказать, что возмущения ( ошибки) et в классической линейной регрессионной модели образуют белый шум, а в случае их нормального распределения – нормальный ( гауссовский) белый шум.
Степень тесноты связи между последовательностями наблюдений временного ряда y1,y2,…..,yn и y1+t,y2+t,....yn+t (сдвинутых относительно друг от друга на e единиц, или, как говорят, с лагом t) может быть определена с помощью коэффициента корреляции
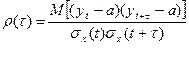 (6.4)
(6.4)
ибо 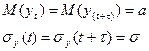
Так как коэффициент r(t) измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость r(t) – автокорреляционной функцией. В силу стационарности временного ряда yt (t= 1,2,…,n) автокорреляционная функция r(t) зависит только от лага t, причем корреляционная функция r( - t) = r(t) , т.е. при изучение r(t) можно ограничиться рассмотрением только положительных значений t.
Статистической оценкой r(t) является выборочный коэффициент автокорреляции r(t), определяемый по формуле коэффициента корреляции (3.20), в которой xi = yt , yi = yt+t , a n заменяется на n - t:
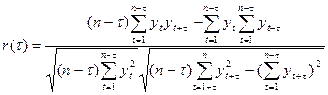
Функцию r(t) называют выборочной автокорреляционной функцией, а ее график - коррелограммой.
При расчете r(t) следует помнить, что с увеличением t число n - t пар наблюдений yt ,yt+t уменьшается, поэтому лаг t должен быть таким, чтобы число n - t было достаточным для определения r(t). Обычно ориентируются на соотношение t £ n/4.
Для стационарного временного ряда с увеличением лага t взаимосвязь членов временного ряда yt и yt+t ослабевает и автокорреляционная функция r(t) должна убывать ( по абсолютной величине). В тоже время для ее выборочного (эмпирического) аналога r(t), особенно при небольшом числе пар наблюдений n - t , свойство монотонного убывания, ( по абсолютной величине) при возрастании t может нарушаться.
Наряду с автокорреляционной функцией при исследовании стационарных временных рядов рассматривается частная автокорреляционная функция rчаст(t), где rчаст(t) есть частный коэффициент корреляции между членами временного ряда yt и yt+t при устранении ( элиминировании) влияния промежуточных ( между yt и yt+t ) членов.
Статистической оценкой rчаст(t) является выборочная частная автокорреляционная rчаст (t) где rчаст (t) – выборочный частный коэффициент корреляции, определяемый по формуле (5.21) или (5.22).Например, выборочный частный коэффициент автокорреляции 1-го порядка между членами временного ряда yt и yt+t при устранении влияния yt+1 может быть вычислен по формулу (5.22):
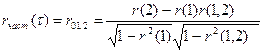


 где r(1) , r (1,2),r(2) – выборочные коэффициенты автокорреляции между yt и yt+1, yt+1 и yt+2, yt и yt+2, t = 1,….,n.
где r(1) , r (1,2),r(2) – выборочные коэффициенты автокорреляции между yt и yt+1, yt+1 и yt+2, yt и yt+2, t = 1,….,n.
►Пример 6.1. По данным табл. 6.1 для временного ряда yt найти среднее значение, среднее квадратическое отклонение, коэффициенты автокорреляции 1-го порядка.
Решение. Среднее значение временного ряда находим по формуле (6.2):
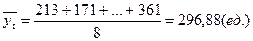
Дисперсию и среднее квадратическое отклонение можно вычислить по формуле (6.3), но в данном случае проще использовать соотношение
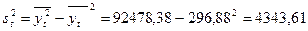
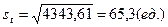
где 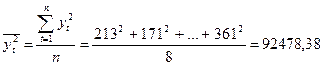
Найдем коэффициент автокорреляции r(t) временного ряда ( для лага t = 1), т.е. коэффициент корреляции между последовательностями семи пар наблюдений yt и yt+t (t = 1,2….,7):
| yt | |||||||
| yt+t |
Вычисляем необходимые суммы:
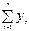 = 213 + 171+….+ 351 = 2014
= 213 + 171+….+ 351 = 2014
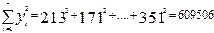
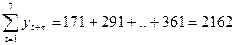
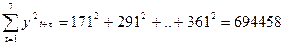
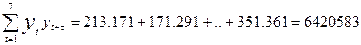 .
.
Теперь по формуле (6.5) коэффициент автокорреляции
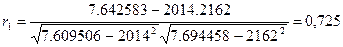
Коэффициент автокорреляции r(2) для лага t = 2 между членами ряда yt и yt+t (t = 1,2,…6) по шести парам наблюдений вычисляем аналогично: r(2)=0,842.
Для определения частного коэффициента корреляции 1-го порядка rчаст(2) = r02.1 между членами ряда yt и yt+t вначале найдем ( по ананогии с предыдущим ) коэффициент автокорреляции r(1,2), между членами ряда yt+1 и yt+t2 : r = (1,2) = 0,85 , а зачем вычислим rчаст(2) по формуле (6.6):
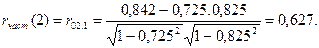 ►
►
Значение автокорреляционных функций r(t) и rчаст(t) может оказать существенную помощь при подборе и идентификации модели анализируемого временного ряда и статистической оценке его параметров ( см. об этом дальше).
Дата добавления: 2016-05-16; просмотров: 1170;
