Применение МНК для нелинейных моделей.

В моделях, нелинейных по оцениваемым параметрам, приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в моделях и линейных, нелинейных по переменным, при оценке параметров исходят из критерия 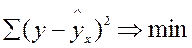, то в моделях нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, то есть 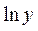, . 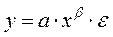Так в степенной функции МНК применяется к преобразованному уравнению .

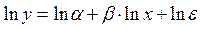Это означает, что оценка параметров основывается на минимальной сумме квадратов отклонений в логарифмах

.

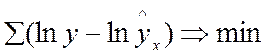Соответственно если в линейных моделях (включая нелинейные по переменным) 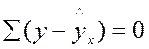, то в моделях, нелинейных по оцениваемому параметру:

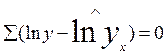, а .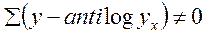

Вследствие этого, оценка параметров для линеаризуемых функций МНК оказывается несколько смещенной.

Например, 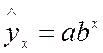(показательная кривая) или 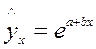(экспонента). Прологарифмируем,

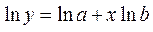
Применяя МНК, минимизируем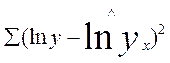

.

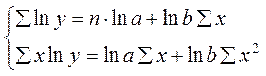
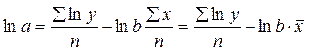Пусть 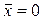. Тогда 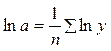или 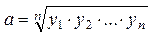, то есть параметр а – есть средняя геометрическая значений у; а в линейной зависимост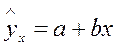и , при 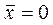. 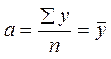- то есть среднее арифметическое.

Так как среднее арифметическое больше среднегеометрического, то оценки, полученные из минимизации 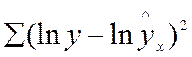будут несколько смещены (занижены).