Оценка степени тесноты связи между количественными переменными.
Среди нелинейных функций, которые могут быть приведены к линейному виду, степенная функция 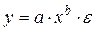 , связано это с тем, что параметр b имеет чёткое экономическое истолкование, то есть он является коэффициентом эластичности.
, связано это с тем, что параметр b имеет чёткое экономическое истолкование, то есть он является коэффициентом эластичности.
Это значит, что b показывает, на сколько % изменится в среднем результат, если фактор изменится на 1%. Рассмотрим пример 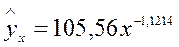
Зависимость спроса от цен, с увеличением цен на 1% спрос снижается на 1,12%.
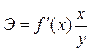
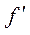 - первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Для степенной функции 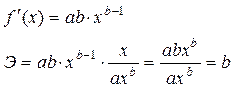 .
.
Коэффициент эластичности можно определить и для других форм связи, то только для степеней функции он представляет собой постоянную величину = b.
Для  .
.
В силу того, что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то рассчитываем средний показатель эластичности:
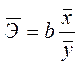 .
.
Для оценки  применяется МНК
применяется МНК
к уравнению 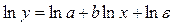
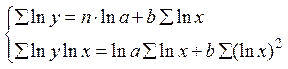
b – определяется из системы, а «а» - косвенным путем, после потенцирования величины ln a.
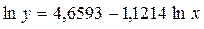
Например,
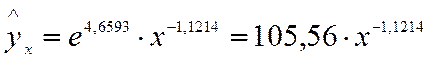
Поскольку а – экономически не интерпретируется, то нередко зависимость остаётся в виде логарифмически линейной. В виде степенной функции изучаем не только спрос, но и предложение.
Обычно эластичность спроса: b<0, а эластичность предложения: b>0.
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчёт экономического смысла не имеет. Например, тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в %. Вряд ли кто будет определять на сколько % может измениться зарплата с ростом стажа работы на 1%. Или на сколько % изменится урожайность пшеницы, если качество почвы измеряемое в баллах, изменится на 1%.
Изучая соотношение ставок межбанковского кредита (у) в % и срока его предоставления в днях (х), получено УР.

Э=0,352% лишён смысла ибо срок предоставления не изменяется в %.
При использовании для этой же задачи линейной зависимости
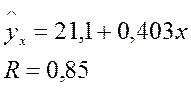
b=0,403 в % показывает изменение ставок кредита с увеличением срока их предоставления на 1 день.
Практическое применение экспоненты возможно, если результативный признак не имеет отрицательных значений. Поэтому, если исследуется, например, финансовый результат деятельности предприятий, среди которых наряду с прибыльными есть и убыточные, то данная функция не может быть использована.
Табл. Коэффициенты эластичности для ряда математических функций.
| Вид функции, у | Первая производная,
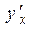
| Коэффициент эластичности,
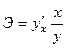
|
Линейная

| b | 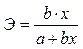
|
Парабола второго порядка 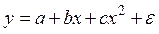
| b+2cx | 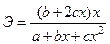
|
Гипербола
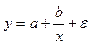
| 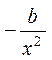
| 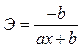
|
Показательная
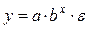
| 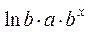
| 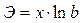
|
Степенная
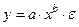
| 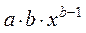
| 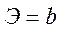
|
Полулогарифмическая 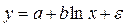
| 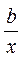
| 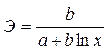
|
Логистическая
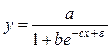
| 
| 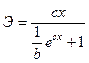
|
Обратная
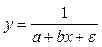
| 
| 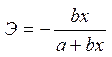
|
При исследовании взаимосвязей среди функций использующих ln y, в эконометрике преобладают степенные зависимости – это и кривые спроса и предложения, а также кривые Энгеля и производственные функции, и кривые освоения для характеристики связи между трудоёмкостью продукции и масштабами производства в период освоения нового вида изделий, и зависимость валового национального дохода от уровня занятости.
В отдельных случаях может использоваться и нелинейная модель  , так называемая обратная модель, является разновидностью гиперболы.
, так называемая обратная модель, является разновидностью гиперболы.
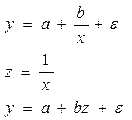
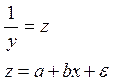
внутренне нелинейна МНК для обратных величин.
МНК:
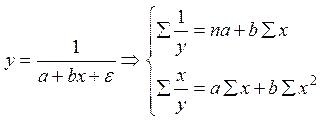
Данное уравнение отражает обратную связь рассмотренных признаков, линейно относительно  .
.  имеет экономический смысл, b - интерпретируется как для линейной зависимости средний прирост.
имеет экономический смысл, b - интерпретируется как для линейной зависимости средний прирост.
Уравнение вида 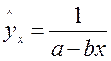 характеризует прямую зависимость результативного признака от фактора. Оно целесообразно при медленном повышении уровней результативного признака с ростом значений фактора. Возможно: 1) логарифмирование
характеризует прямую зависимость результативного признака от фактора. Оно целесообразно при медленном повышении уровней результативного признака с ростом значений фактора. Возможно: 1) логарифмирование
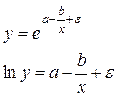
2) преобразование в обратные величины
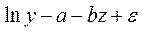


Функция насыщения. Используется для анализа стат.данных о бюджетах потребителей и др.
Для показательной функции 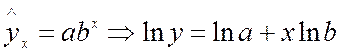 , доверительный интервал для параметра b:
, доверительный интервал для параметра b:

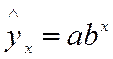 - строят доверительные интервалы.
- строят доверительные интервалы.
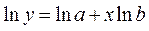 , для
, для 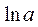 и
и 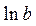 , а далее с помощью обратного преобразования доверительные преобразования для а и b.
, а далее с помощью обратного преобразования доверительные преобразования для а и b.
Для степенной  строится как в линейной.
строится как в линейной.
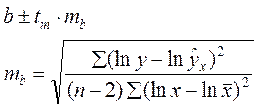
Дата добавления: 2016-05-16; просмотров: 1246;
