Анализ временного ряда на основе автокорреляционной модели
Модель
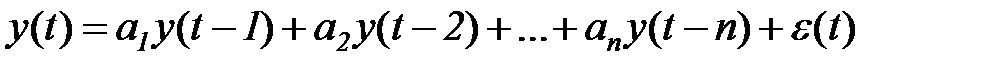 (5.76)
(5.76)
называется моделью авторегрессионного процесса и обозначается 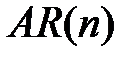 , где n – максимальный учитываемый лаг.
, где n – максимальный учитываемый лаг.
Стационарный процесс n-го порядка характеризуется постоянными значениями всех своих моментов порядка n и ниже. У строго стационарных процессов постоянными являются моменты всех порядков. Например, для любых двух интервалов времени (T1, T2) и (T3, T4) для стационарного процесса второго порядка должны выполняться условия равенства на рассматриваемых интервалах математических ожиданий, дисперсий и коэффициентов автокорреляций одинакового порядка.
Для проверки статистических гипотез о равенстве этих величин используются критерии Стьюдента, Фишера и другие.
Построение модели AR(n) типа (5.76), адекватной реальному временному ряду 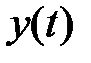 ,
, 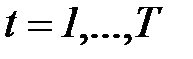 , предполагает решение двух взаимосвязанных задач: определение порядка модели n и оценка значений ее коэффициентов.
, предполагает решение двух взаимосвязанных задач: определение порядка модели n и оценка значений ее коэффициентов.
При определении порядка модели необходимо учитывать, что с увеличением лага на единицу число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. Поэтому обычно максимальный порядок коэффициента автокорреляции равен N/4, где 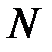 - длина анализируемого ряда.
- длина анализируемого ряда.
Лаг L, при котором автокорреляция 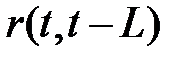 максимальна, определяет структуру временного ряда. Если максимум соответствует L=1, то исследуемый ряд содержит только тенденцию. Если L>1, то ряд содержит (помимо тенденции) колебания периодом L. Если ни один из
максимальна, определяет структуру временного ряда. Если максимум соответствует L=1, то исследуемый ряд содержит только тенденцию. Если L>1, то ряд содержит (помимо тенденции) колебания периодом L. Если ни один из 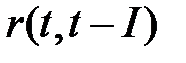 ,
, 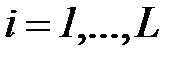 не является значимым, можно сделать одно из предположений:
не является значимым, можно сделать одно из предположений:
- временной ряд не содержит тенденций и циклических колебаний, а его уровень определяется случайной компонентой;
- временной ряд содержит нелинейную тенденцию, для выявления которой необходимы дополнительный анализ.
Без ограничения общности в дальнейшем будем предполагать, что математическое ожидание ряда 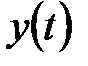 равно нулю (
равно нулю ( 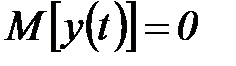 ). Если это не так, то вместо переменной
). Если это не так, то вместо переменной 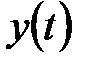 в выражении (5.76) можно рассмотреть центрированную переменную
в выражении (5.76) можно рассмотреть центрированную переменную 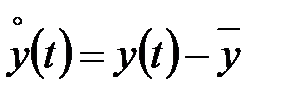 , где
, где 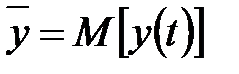 , при этом
, при этом 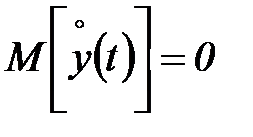 . Если временной ряд имеет тренд, то из значений ряда необходимо вычесть трендовую составляющую.
. Если временной ряд имеет тренд, то из значений ряда необходимо вычесть трендовую составляющую.
Из выражения (4.76) следует, что параметры модели ai, 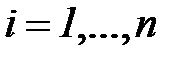 могут быть выражены через коэффициенты автокорреляции:
могут быть выражены через коэффициенты автокорреляции:
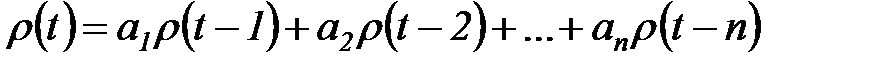 (5.77)
(5.77)
которое связывает коэффициенты автокорреляции процесса 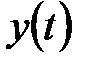 и коэффициенты модели
и коэффициенты модели 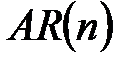 . Подставив в (5.77) вместо значений коэффициентов автокорреляции
. Подставив в (5.77) вместо значений коэффициентов автокорреляции 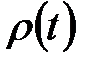 процесса
процесса 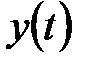 их выборочные оценки
их выборочные оценки 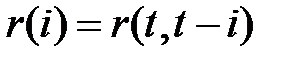 ,
, 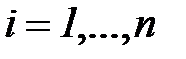 , получим следующую систему линейных уравнений
, получим следующую систему линейных уравнений
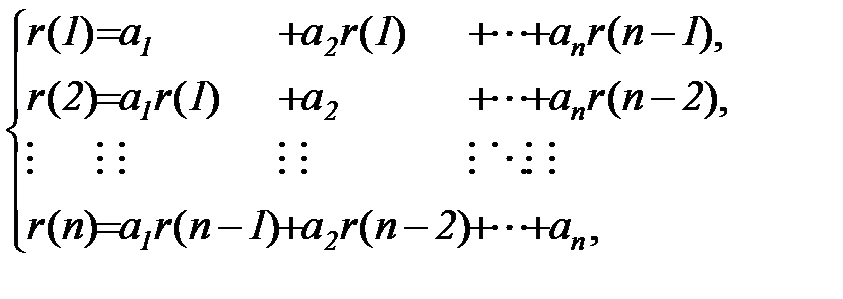 (5.78)
(5.78)
в которой известными являются оценки коэффициентов автокорреляции 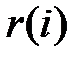 ,
, 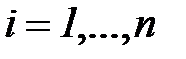 , а неизвестными – оценки коэффициентов модели
, а неизвестными – оценки коэффициентов модели 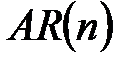
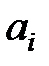 ,
, 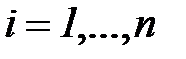 .
.
Поясним, как систему (4.78) можно получить из (5.76). Умножим обе части (5.76) на 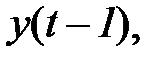 вычислим математическое ожидание и результат разделим на
вычислим математическое ожидание и результат разделим на 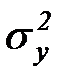 (предполагается, что ряд стационарный). В результате получим первое уравнение системы (5.78). Повторив описанную операцию с
(предполагается, что ряд стационарный). В результате получим первое уравнение системы (5.78). Повторив описанную операцию с 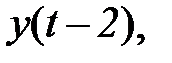 получим второе уравнение системы, и так далее.
получим второе уравнение системы, и так далее.
Систему (5.78) называют уравнениями Юла-Уокера, а полученные на их основе значения 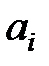 ,
, 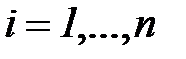 - оценками коэффициентов модели авторегрессии
- оценками коэффициентов модели авторегрессии 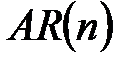 Юла-Уокера. Решение уравнения (5.78) можно представить в матричной форме:
Юла-Уокера. Решение уравнения (5.78) можно представить в матричной форме:
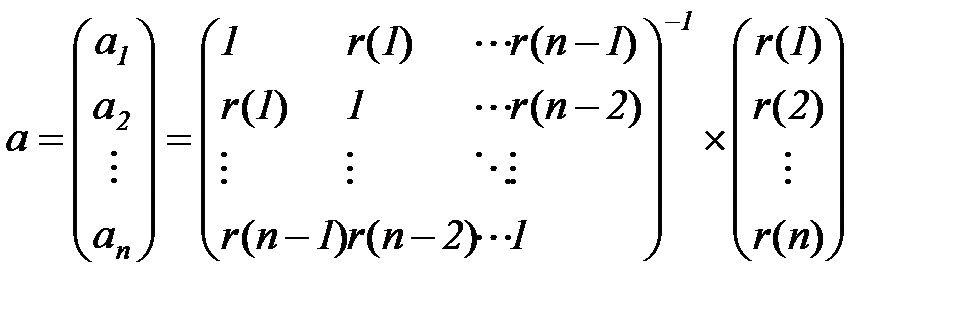 . (5.79)
. (5.79)
Теоретически оценки Юла-Уокера должны обладать свойствами несмещенности и эффективности. Однако, на практике, в моделях авторегрессии высокого порядка эти свойства могут не подтвердиться. Особенно это относится к свойству несмещенности. Смещенность в оценках коэффициентов авторегрессии может быть обусловлена существующей зависимостью между сдвинутыми рядами переменной 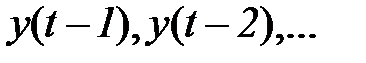 и ошибкой
и ошибкой 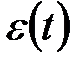 . Этой возможной зависимостью при построении системы уравнений Юла-Уокера обычно пренебрегают, полагая
. Этой возможной зависимостью при построении системы уравнений Юла-Уокера обычно пренебрегают, полагая 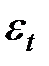 «белым шумом».
«белым шумом».
Неэффективность оценок может быть вызвана плохой обусловленностью матрицы 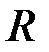 :
:
 ,
,
(определитель матрицы близок к нулю), что, как правило, является свидетельством зависимости между рядами 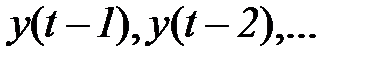 .
.
Целесообразность использования моделей авторегрессии при анализе закономерностей временного ряда обычно устанавливается сравнением дисперсии исходного процесса sy2 и дисперсии ошибки модели se2
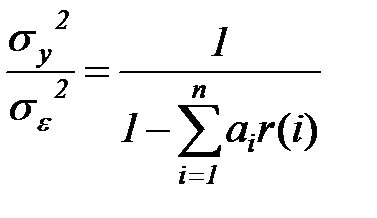 . (5.80)
. (5.80)
Модель авторегрессии считается «достаточно хорошей», если 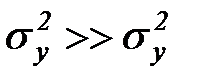 , т.е. когда дисперсия ошибки модели много меньше дисперсии процесса.
, т.е. когда дисперсия ошибки модели много меньше дисперсии процесса.
Частными случаями модели авторегрессии являются модели первого порядка 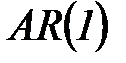 и второго порядка
и второго порядка 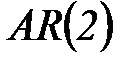 .
.
Модель авторегрессии первого порядка 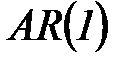 записывается в виде
записывается в виде
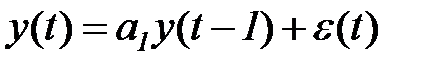 . (5.81)
. (5.81)
Из системы Юла-Уокера (5.78) следует, что
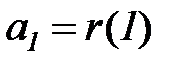 , (5.82)
, (5.82)
а из (5.81) вытекает, что
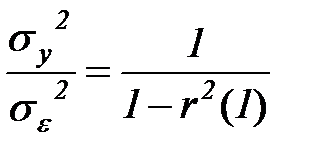 . (5.83)
. (5.83)
Из (5.83) следует, что с ростом абсолютных значений 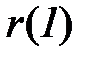 точность описания процесса
точность описания процесса 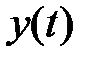 моделью авторегрессии первого порядка увеличивается, а с его снижением – уменьшается.
моделью авторегрессии первого порядка увеличивается, а с его снижением – уменьшается.
Модель авторегрессии второго порядка AR(2) записывается в виде:
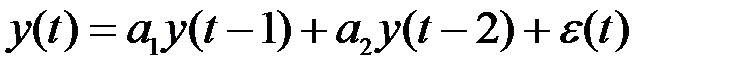 . (5.84)
. (5.84)
Из системы Юла-Уокера следует
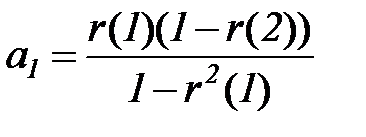 ,
, 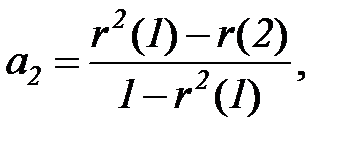 (5.85)
(5.85)
а из (5.84) вытекает, что
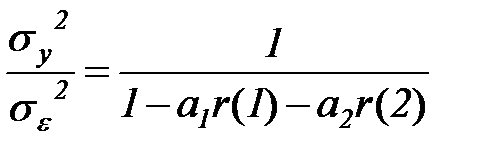 . (4.86)
. (4.86)
При практическом применении авторегрессионных моделей 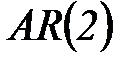 соотношение
соотношение 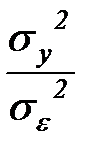 обычно не превосходит 5 : 1.
обычно не превосходит 5 : 1.
Пример. Пусть имеются поквартальные данные об объемах выпуска некоторого товара на предприятии (в тыс. шт.) за 3 года (таблица 5.1). Требуется определить структуру данного временного ряда и построить модель для прогнозирования значений ряда.
Графическое представление ряда приведено на рисунке 5.16. Видно, что данный ряд, во-первых, имеет временной тренд, а, во-вторых, в нем явно присутствует периодическая составляющая с периодом в 4 квартала (1год).

Рисунок 5.16. График исходного временного ряда 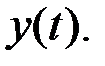
Первым этапом анализа ряда будет выявление тренда. Примем гипотезу о том, что тренд линейный, т.е. может быть представлен уравнением
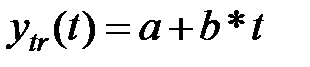 , (5.87)
, (5.87)

где 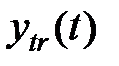 - значение тренда,
- значение тренда, 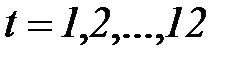 – значения независимой переменной (времени),
– значения независимой переменной (времени), 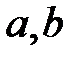 – коэффициенты.
– коэффициенты.
Воспользовавшись методом наименьших квадратов (его описание приведено в разделе 7.2.1 настоящего пособия), на основе данных таблицы 5.1 получим следующие выражения для коэффициентов
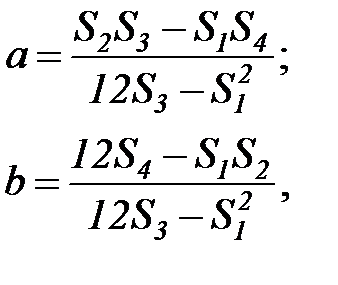 (5.88)
(5.88)
где суммы 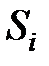 вычисляются по формулам
вычисляются по формулам
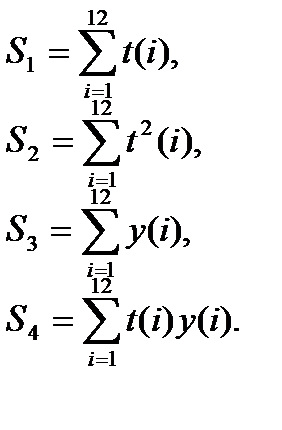
Проделав вычисления, получим 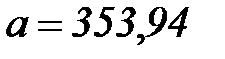 ,
, 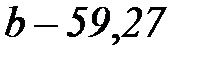 .
.
Вычтя значения тренда (5.87) из исходных данных таблицы, получим «очищенные» значения временного ряда 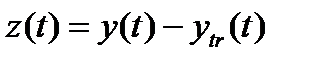 , которые также приведены в таблице 5.1. Нетрудно убедиться, что новая переменная
, которые также приведены в таблице 5.1. Нетрудно убедиться, что новая переменная 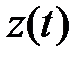 является центрированной, поскольку сумма
является центрированной, поскольку сумма 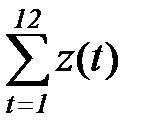 близка к нулю.
близка к нулю.
Таблица 5.1
Данные предприятия об объемах выпуска товара в тысячах штук
| Год | Квартал | t | Объем выпуска 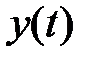
| 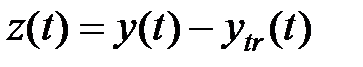
| Прогноз 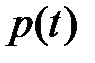 по формуле (4.90) по формуле (4.90)
|
| -3,2 | - | ||||
| -72,4 | - | ||||
| - | |||||
| - | |||||
| -70,3 | -43,6 | ||||
| -159,5 | -103,7 | ||||
| 206,2 | 170,3 | ||||
| -28 | 37,9 | ||||
| -122,3 | -42,3 | ||||
| -226,5 | -131,5 | ||||
| 229,1 | 243,0 | ||||
| 34,9 | 38,7 |
Приступим теперь к построению прогнозирующей функции. Для этого по выражениям (5.72) – (5.75) рассчитаем коэффициенты автокорреляции порядков с 1 по 5. Результаты расчетов представлены в таблице 5.2. Проверка значимости отличия коэффициентов автокорреляции от нуля проводим по критерию Стьюдента. Результаты проверки при 5% уровне значимости представлены в этой же таблице.
На основе таблицы 5.2 можно сделать вывод о том, что в ряду динамики, представленном в таблице 5.1, имеются периодические колебания с периодом равным 4, что подтверждается проведенным ранее визуальным анализом графика 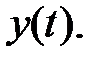
Таблица 5.2
Коэффициенты автокорреляции 1 – 5 порядков
| Лаг L (порядок) | |||||
Коэффициент автокорреляции 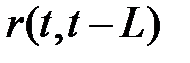
| -0,2357 | -0,4451 | -0,3192 | 0,9410 | -0,2872 |
| Число степеней свободы критерия Стьюдента | |||||
| Расчетное значение критерия Стьюдента, t | 1,9 | 0,8 | 1,3 | 20,4 | 0,9 |
| Критическое значение критерия Стьюдента, при 5% уровне значимости | 2,7 | 2,8 | 2,8 | 3,0 | 3,2 |
| Отличие коэффициента автокорреляции от нуля | не значимо | не значимо | не значимо | значимо | не значимо |
Итак, модель для прогноза в соответствии с изложенной выше теорией будем искать в виде
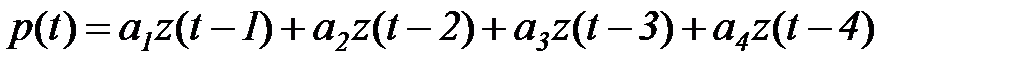 , (5.89)
, (5.89)
где 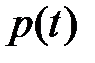 - прогноз значения функции
- прогноз значения функции 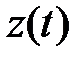 , причем коэффициенты
, причем коэффициенты 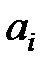 ,
, 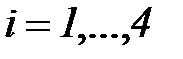 определятся выражением (5.79), в котором для наших данных получатся следующие матрицы
определятся выражением (5.79), в котором для наших данных получатся следующие матрицы
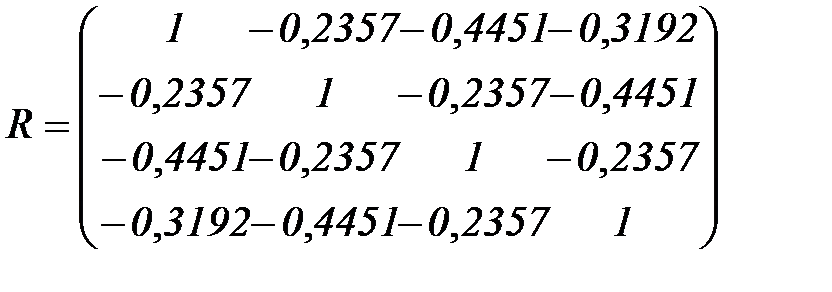 ,
,
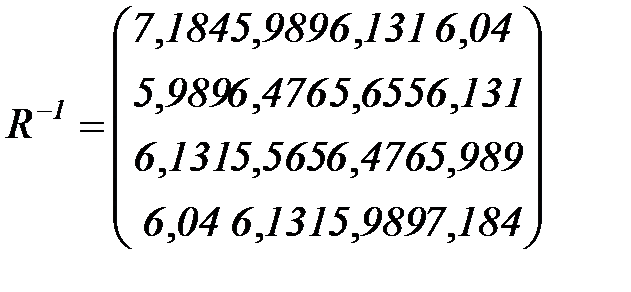 ,
, 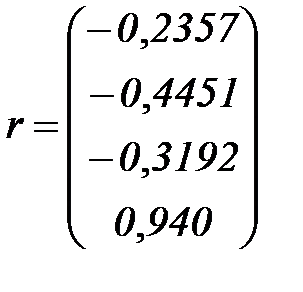 ,
,
откуда получаем вектор коэффициентов модели (5.89):
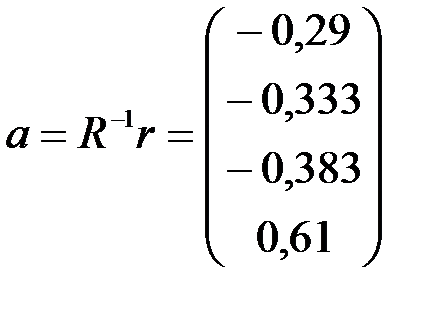
Таким образом, прогнозирующая модель примет вид
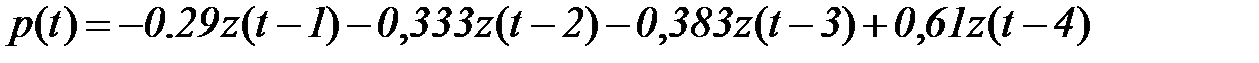 . (5.90)
. (5.90)

Рисунок 5.17. Графики временного ряда: 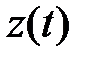 - временной ряд с убранным трендом,
- временной ряд с убранным трендом, 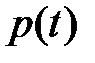 - прогноз временного ряда на один шаг (начиная с
- прогноз временного ряда на один шаг (начиная с 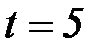 ).
).

Рисунок 5.18 Графики временного ряда: 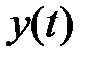 - исходный ряд,
- исходный ряд, 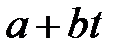 - линия тренда,
- линия тренда, 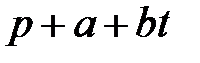 - график прогноза на один шаг с наложенным трендом.
- график прогноза на один шаг с наложенным трендом.
Подставляя в модель (5.90) значения 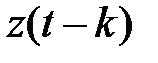 ,
, 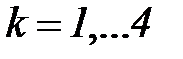 , из таблицы 5.1, получим прогнозные значения величины
, из таблицы 5.1, получим прогнозные значения величины 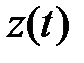 на один шаг вперед. Вычисленные по формуле (5.90) значения прогноза приведены в последнем столбце таблицы 5.1. Поскольку для прогнозирования величины
на один шаг вперед. Вычисленные по формуле (5.90) значения прогноза приведены в последнем столбце таблицы 5.1. Поскольку для прогнозирования величины 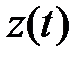 требуются четыре предыдущих значения этого ряда, то прогноз начинается с
требуются четыре предыдущих значения этого ряда, то прогноз начинается с 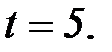 Графики прогнозных значений
Графики прогнозных значений 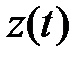 и
и  приведены на рисунке 5.17, 5.18. Анализ этих рисунков говорит о качественно верном прогнозировании хода временного ряда. Отношение дисперсий исходного ряда и ошибки прогноза в соответствии с формулой (5.80) по данным таблицы 5.1 равно
приведены на рисунке 5.17, 5.18. Анализ этих рисунков говорит о качественно верном прогнозировании хода временного ряда. Отношение дисперсий исходного ряда и ошибки прогноза в соответствии с формулой (5.80) по данным таблицы 5.1 равно
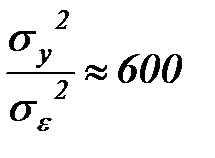 .
.
Полученное отношение подтверждает вывод о достаточно хорошем качестве прогноза.
Глава 6 Моделирование информационных
процессов и систем
При материала данной главы мы будем использовать понятия и математический аппарат, относящиеся к общей теории систем. В общей теории систем такие понятия в силу их общности трактуются не всегда однозначно. Чтобы достичь однозначности в понимании последующего материала, определим эти понятия применительно к информационным системам (ИС) [12].
6.1. Общие определения теории систем
Элемент— это минимальный неделимый объект. Элемент можно использовать только как целое, поэтому недопустимо говорить о половине или четверти элемента. Неделимость элемента — это, прежде всего, удобное понятие, но не физическое свойство. Оперируя понятием «элемент», исследователь оставляет за собой право перейти на другой уровень рассмотрения вопросов и говорить о том, из чего состоит элемент, а это свидетельствует о физической разложимости последнего. Таким образом, объекты называются элементами по соглашению, принимаемому с целью дать ответ на определенные вопросы, стоящие перед исследователями. Изменение вопросов может потребовать разложения элементов на составные части или объединения нескольких элементов в один.
Система— это совокупность связанных элементов, объединенных в одно целое для достижения определенной цели. Здесь под целью понимается совокупность результатов, определяемых назначением системы. Наличие цели и заставляет связывать элементы в систему. Целостность — наиболее важное свойство системы. Элемент принадлежит системе потому, что он связан с другими ее элементами, так что множество элементов, составляющих систему, невозможно разбить на два и более несвязанных подмножества. Удаление из системы элемента или совокупности элементов непременно изменяет ее свойства в направлении, отличном от цели. Искусственные (инженерные) системы описывают путем определения их функций и структур.
Функция системы— это правило получения результатов, предписанных целью (назначением) системы. Определяя функцию системы, ее поведение описывают с использованием некоторой системы понятий — отношений между переменными, векторами, множествами и т. п. Функция устанавливает, что делает система для достижения поставленной цели безотносительно к физическим средствам (элементам, связям), составляющим саму систему, и не определяет, как устроена система. Системы изучают на разных уровнях абстракции, с использованием различных подходов, каждый из которых дает ответ на определенные вопросы. В связи с этим функции системы могут описываться с разной степенью детализации. Для описания функций систем используются различные теории: теория множеств, теория алгоритмов, теория случайных процессов, теория информации и другие. Функционировать – значит реализовать функцию, т. е. получать результаты, предписанные назначением системы.
Структура системы – это фиксированная совокупность элементов и связей между ними. В общей теории систем под структурой принято понимать только множество связей между элементами, т. е. структура понимается как картина, отображающая только конфигурацию системы безотносительно к составляющим ее элементам. Такое толкование ее понятия удобно при структурном подходе к изучению свойств различных систем — систем с параллельными, последовательными, иерархическими структурами, обратными связями и т. п. На практике в понятие «структура» включают не только множество связей, но и множество элементов, между которыми существуют связи. Этот смысл отражен в данном определении структуры. Наиболее часто структура системы изображается в форме графа: элементы системы представляются вершинами графа, а связи – дугами (ребрами) графа. Граф – это математическая форма отображения структур. Инженерной формой изображения структур систем являются схемы. Схема и граф – понятия адекватные по содержанию, но различные по форме. В схемах элементы и связи обозначаются любыми фигурами, удобными для инженерных (производственных) применений.
Организация – это способ реализации определенных функций в системах, состоящих из большого числа элементов. Обычно к одной и той же цели можно, прийти различными способами, исходя из различных принципов организации систем. Каждый принцип организации задает определенный способ построения множества систем, аналогичных по назначению, но различных по функциям и структурам. Конкретная система представляет собой лишь пример реализации некоторого способа организации. Например, подавляющее большинство современных ЭВМ строится на основе одного принципа организации – принципа программного управления реализацией алгоритма на основе команд, имеющих операционно-адресную структуру. Таким образом, организация – понятие более высокого ранга, чем функция и структура; организация – это модель, на основе которой могут строиться многие конкретные системы.
Если речь идет о способе порождения функций, достаточных для достижения определенной цели (определенных результатов), то используется термин функциональная организация. Если же речь идет о наборе элементов и способе их соединения в структуру, обеспечивающую реализацию функций определенного класса, то используется термин структурная организация.Определяя некоторый способ функциональной организации, выявляют класс функций, присущих системам определенного назначения (безотносительно к средствам, необходимым для реализации этих функций), а, определяя способ структурной организации, выявляют правило построения структур, реализующих некоторый класс функций, т.е. отвечающих некоторому назначению.
Анализ – это процесс определения свойств, присущих системе. Типичная задача анализа состоит в следующем. Известны функции и характеристики элементов, входящих в состав системы, и определена структура системы. Необходимо определить функции или характеристики, присущие совокупности элементов в целом.
Синтез – это процесс порождения функций и структур, необходимых и достаточных для получения определенных результатов. Выявляя функции, реализуемые системой, определяют некоторую абстрактную систему, о которой известно только то, что она будет делать. В связи с этим этап синтеза функций называется абстрактным синтезом, а этап порождения структуры, реализующей заданные функции, — структурным синтезом.
Эффективность – это степень соответствия системы своему назначению. Из двух систем более эффективной считается та, которая лучше соответствует своему назначению. Оценка эффективности системы — одна из задач анализа систем.
Показатель эффективности(качества) – это мера одного свойства (характеристики) системы. Показатель эффективности всегда имеет количественный смысл, т. е. является измерением некоторого свойства. По этой причине использование некоторого показателя эффективности предполагает наличие способа измерения (оценки) значения этого показателя. Для оценок эффективности систем могут применяться, например, такие показатели, как производительность, стоимость, надежность, габариты и т. п.
Критерий эффективности – это мера эффективности системы. Критерий эффективности имеет количественный смысл и измеряет степень эффективности системы, обобщая все ее свойства в одной оценке — значении критерия эффективности. Эффективность систем, создаваемых для одной цели, оценивается на основе одного критерия, общего для этого класса систем. Различие в назначениях систем предполагает, что для оценки эффективности таких систем используются различные критерии. Если при увеличении эффективности значение критерия возрастает, то критерий называется прямым; если значение критерия уменьшается, то инверсным. Из двух систем более эффективной считается та, которой соответствует большее значение прямого критерия (меньшее значение инверсного критерия).
6.2 Методология описания информационных систем
Высокая стоимость современных информационных систем (ИС) и их влияние на эффективность деятельности предприятий вынуждают вкладывать немалые средства в методологии, дающие уверенность в качестве конечного результата. При этом понятно желание найти средства, универсально решающие все или почти все проблемы построения информационных систем. К сожалению, таких средств не существует. Каждый метод и поддерживающие его инструментальные средства имеют свою область применения, свои недостатки и ограничения [5].
Методология построения ИС содержит три компонента (рис.6.1):
· набор типов моделей для описания требований к ИС, проектных и программных решений. Каждая модель обычно содержит как определение конструкций (нотацию), так и правила их использования (синтаксис);
· методика применения набора моделей для построения ИС. Методика обычно использует фиксированный набор моделей и определяет последовательность их построения для описания различных аспектов создаваемой системы;
· процесс организации проектных работ. Включает различные технологии - планирования, управления проектом, контроля качества и т.д.
| Набор моделей (нотация и синтаксис) |
| методика применения набора моделей |
| процессорганизации проектных работ |
| Методология построения ИС |
Рисунок 6.1. Три компонента методологии построения ИС
Каждая из набора моделей описания ИС представляет полное и самодостаточное упрощенное представление действительности, созданное с известной прикладной целью исследования
При этом модель определяется как изображение существенных сторон реальной системы, в удобной форме отражающее информацию о системе.
В самом общем виде модель может быть описана набором
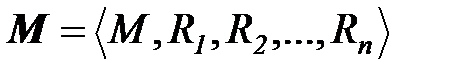 ,
,
где М - несущее множество элементов (универсум), 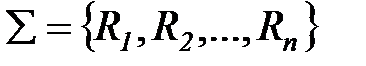 - сигнатура модели М, описывающая заданные на множестве М отношения R.
- сигнатура модели М, описывающая заданные на множестве М отношения R.
Естественным представляется использование совокупности моделей, отражающих различные абстракции описания системы, разнообразные аспекты ее поведения, этапы (итерации) ее эволюции в процессе функционирования. Каждая из моделей имеет уникальные свойства, отсутствующие у других, и поэтому в различной степени соответствует реальной системе. Рассматривая совокупность моделей как единый набор инструментов, аналитик выбирает необходимые ему для решения конкретной задачи исследования. Используемая модель, в свою очередь, определяет и то, как будет осмысливаться проблема и какие решения будут приниматься.
Модель - инструмент и результат исследования, а моделирование - процесс исследования реальной системы путем итеративного изменения изображений, интерпретирующих ее существенные стороны с целью получения информации о их свойствах.
Решение задачи анализа путем моделирования подразумевает определение того, обладает ли модель, представляющая систему, заданными свойствами.То есть в процессе анализа по модели системы строится ее эквивалент, интерпретирующий исследуемое свойство системы.
6.3 Моделирование реальности в информационных системах
Статические и динамические модели. Создание информационных систем с целью поддержания деятельности в какой-либо сфере позволяет лицу, занимающемуся этой деятельностью, взаимодействовать не с реальными объектами предметной области системы, а с информационной системой, не покидая своего рабочего места. Такой подход позволяет получать сведения о состоянии сущностей и процессов предметной области ИС не путем непосредственных измерений (наблюдений) в реальном мире, а используя информационную модель. Достоинство модельного подхода состоит в том, что он предоставляет возможности для анализа и оценки последствий различных управленческих решений без проведения натурного эксперимента.
Важную роль в моделировании предметной области ИС играют ее информационные ресурсы, подробно рассмотренные нами в первой главе. Во всех классах моделей, рассматриваемых ниже, информационные ресурсы системы представляют статическую модель предметной области, характеризуя ее текущее состояние. Темпоральные базы данных позволяют представлять динамику предметной области — изменение ее состояния во времени. Следует заметить, что с элементами коллекции информационных ресурсов, представляющих статическую модель предметной области, могут ассоциироваться некоторые отметки времени, но эти временные характеристики могут воспринимать только пользователи. Системные механизмы оперировать ими не способны. Такие отметки времени принято называть временем, определяемым пользователем. Например, документы в системе текстового поиска могут быть датированными. Но система воспринимает указанную дату как обычный фрагмент текста.
| Моделирование реальности в информационных системах |
| По информационным ресурсам |
| По степени структурированности данных |
| По уровню абстракции |
| Статические |
| Темпоральные |
| Структурированные |
| Слабоструктурированные |
| Формальные |
| Экстенсиональные |
| Интесиональные |
| Неструктурированные |
Рис.6.2. Классификация моделей, используемых в информационных системах
Точно так же, как обстоит дело с характеристиками времени, во всех распространенных классах моделей, за исключением объектных, информационные ресурсы не моделируют поведенческие аспекты предметной области. Эта функция выполняется компонентами приложения ИС. В таких случаях приложение фактически интегрируются с информационной системой, и трудно провести разделяющие их границы.
Природа моделей предметной области, поддерживаемых в ИС, может быть различной. С технологической точки зрения наиболее существенны различия подходов к моделированию предметной области по степени структурированности ее представлений, которую они обеспечивают (рис.5.2). Используемые в настоящее время подходы к моделированию предметной области в ИС охватывают следующий спектр возможностей.
Структурированные модели. Модели такого рода основаны на выявлении регулярной структуры предметной области. Для конструирования таких моделей нужно типизировать сущности предметной области, относя их к одному типу сущности с одинаковым набором свойств. Аналогичным образом типизируются связи между сущностями. Связи определяются на множествах типов сущностей и могут иметь различную арность. Например, связи могут быть бинарными или n-арными. Представление предметной области, сконструированное с помощью рассматриваемого подхода, также называется структурированным.
Одной из разновидностей рассматриваемого подхода к моделированию предметной области является объектный (или объектно-ориентированный) подход, который дает возможность моделировать не только структуру предметной области, но и поведение экземпляров сущностей, относящихся к каждому определенному типу [22]. С этой целью определение каждого типа сущностей включает определения допустимых на его экземплярах операций (или методов).
При использовании структурированных моделей представление предметной области имеет два уровня. Представление более высокого уровня абстракции — это модель предметной области, отображающая ее свойства, инвариантные во времени. Эта модель представляется в терминах типов сущностей предметной области и типов связей между ними. Такую модель называют интенсионалом предметной области (рис.6.2). Второй, более конкретный уровень, моделирует состояние предметной области в зависимости от времени. Модель этого уровня представляется в терминах конкретных экземпляров сущностей и связей определенных типов между ними. Эту модель называют экстенсионалом предметной области.
На структурированных моделях предметной области с регулярной структурой основаны системы баз данных. В этом случае интенсионал предметной области называют схемой базы данных. Естественно называть информационные ресурсы систем баз данных структурированными данными.
Слабоструктурированные модели. При создании некоторых информационных систем применяется подход к моделированию предметной области, при котором регулярная ее структура не определена, или она не существует в рассматриваемом случае. Такой подход используется, например, в системах, основанных языках разметки.
В рассматриваемом подходе не предусматривается строгая типизация сущностей предметной области и связей между сущностями. Представление предметной области обычно является одноуровневым. Поддерживается экстенсионал предметной области — ее представление в терминах конкретных экземпляров сущностей и связей между ними. Иногда предпринимается попытка некоторой типизации сущностей и связей. Но не гарантируется, что свойства типов обязательно присущи всем относящимся к ним экземплярам. Определенный в таком случае интенсионал, по аналогии с системами баз данных иногда называемый схемой, не играет директивной роли. Конкретные экземпляры сущностей и связей, свойства которых не соответствуют схеме, системой не отвергаются.
Такого рода представления предметной области называют слабоструктурированными. Информационные ресурсы систем, основанных на рассматриваемом подходе, называют слабоструктурированными данными.
Наиболее известной информационной системой, в которой поддерживается слабоструктурированное представление предметной области, является глобальная распределенная гипермедийная ИС (далее — Web), базирующаяся на технологиях HTML.
Формирующийся в настоящее время Web нового поколения, основанный на технологической платформе XML, позволяет поддерживать не только слабоструктурированные, но и структурированные представления предметной области.
Формальные модели. Такие модели связаны с подходом к моделированию предметной области ИС, основанным на использовании формальных языков. Как и в случае структурированных моделей, здесь определена регулярная структура предметной области, но для модельного ее представления используются формальные языки. Формальное представление предметной области, как и в случае структурированных моделей, является двухуровневым. Оно включает интенсионал и экстенсионал предметной области. Интенсионал представляет собой набор аксиом, описывающий соотношения между его элементами – типами сущностей и связей. В данном контексте они представляются как предметные переменные.
Экстенсионал предметной области представляется в данном случае в виде совокупности фактов.
Для создания формальных моделей обычно используются различные языки представления знаний, чаще всего языки логики первого порядка. В последнее время стала применяться их разновидность – языки логик описаний.
Рассматриваемый подход позволяет осуществлять логический вывод, и пользователь может получать при обращении к системе новые факты, которые непосредственно в явном виде в ней не были представлены. Такие интеллектуальные информационные системы являются представителями класса систем, основанных на знаниях. Они весьма близки по своим возможностям к системам баз знаний, экспертным системам и т.д.
Неструктурированные модели. К этой категории относятся вербальные модели, то есть модели, описывающие реальность в виде текстов на естественном языке. В таких моделях явным образом не представляется структура предметной области — множество сущностей, их свойств, различного рода связей между этими сущностями, интересующих пользователя системы. Эта структура может быть реконструирована на основе анализа содержания заданных текстов, однако, не всегда однозначным образом. Автоматизация такого анализа – достаточно сложная задача, связанная с технологиями обработки естественного языка.
Существует широкий спектр ИС, поддерживающих неструктурированные модели предметной области. В простейших из них задачи анализа и понимания естественного языка возлагаются на пользователя. В продвинутых системах большая часть нагрузки, связанной с решением этих задач, возлагается на систему.
Здесь уместно вспомнить об интенсионале предметной области. В системах рассматриваемого класса он может быть материализован в форме тезауруса, описания онтологии предметной области и других инструментов, которые относятся к средствам лингвистической поддержки системы. В простейших системах он явно не представлен в системе и ей не доступен. Он существует только в интеллектуальном багаже пользователя. Что касается упоминавшихся продвинутых систем, то их возможности по работе с содержанием поддерживаемых в системе документов основаны именно на интенсиональной модели предметной области, явным образом представленной в системе.
Представления предметной области в вербальных моделях можно назвать неструктурированными. Информационные ресурсы таких систем часто называют неструктурированными данными. К числу информационных систем, использующих вербальные модели предметной области, относятся системы текстового поиска.
Модели данных. Для создания структурированных и слабоструктурированных представлений предметной области и выполнения операций в терминах таких представлений служат разнообразные реализованные в программных средствах инструменты моделирования, которые называют моделями данных.
Концепция модели данных родилась в области баз данных и приобрела в ней фундаментальное значение. Не случайно за работы в этой области одной из самых престижных наград в информатике — Тьюринговской премии — были удостоены в разное время идеолог сетевой модели данных CODASYL Чарльз Бахман (1973) и создатель реляционной модели Эдгар Кодд (1981).
В использовании понятия «модель данных» все еще существует путница между инструментами и результатами моделирования.
В современном понимании модель данных — это не результат, а инструмент моделирования, то есть совокупность правил структурирования данных, допустимых операций над ними и видов ограничений целостности, которым они должны удовлетворять. Если перефразировать это определение для случая объектного подхода, то можно сказать, что модель данных – это некоторая система типов данных.
Как мы уже видели, в ИС приходится иметь дело с моделями различных уровней абстракции. С этой точки зрения можно рассматривать модель данных как метамодель для описания интенсиональных моделей предметной области в среде выбранной СУБД или других средств управления данными. Операционные средства модели используются для выполнения различных операций над элементами экстенсиональной модели предметной области – экземплярами данных и связей между ними в базе данных или для формулировки.
В системах базы данных интенсиональная модель предметной области, выраженная с помощью дескриптивных средств модели данных, которая реализована в используемой СУБД, называется схемой базы. данных. Именно на основе той или иной модели данных конструируются механизмы управления данными каждой СУБД.
Материализация моделей предметной области. Возникает естественный вопрос, в каком виде «материализуются» модели предметной области в ИС. Экстенсиональные модели материализуются в виде совокупности информационных ресурсов системы. Что касается интенсиональных моделей, то они материализуются средствами метаданных в виде некоторой спецификации на языке определении данных, формальном языке и т.д., в зависимости от класса системы. Кроме того, в текстовых системах некоторые элементы интенсиональных моделей материализуются в виде средств лингвистической поддержки — тезаурусов, лексических словарей и др.
В последние 20 лет для исследования сложных экономических систем все более широко начали применяться методы синергетики – теории самоорганизации сложных систем [5]. Такие системы характеризуются тем, что у них возникают свойства, отсутствующие у составляющих их элементов.
До 60-х годов XX века предполагалось, что есть два класса процессов. К первому классу относились процессы, которые описываются динамическими системами, где будущее однозначно определяется прошлым (детерминированные системы). Предполагалось, что для них имеется полная предсказуемость, и мы можем заглянуть как угодно далеко в будущее и как угодно далеко в прошлое. Второй класс процессов – это процессы, где будущее не зависит от прошлого и определяется чисто случайными факторами (стохастические системы).
В 70-е годы прошлого века стало понятно, что есть третий класс процессов, которые формально описываются динамическими системами, но при этом их поведение может быть предсказано только на небольшом интервале времени.
Были пересмотрены взгляды на принципиальную возможность предсказуемости. В 1963 году был введен термин горизонта прогноза или пределов предсказуемости. Для существования горизонта прогноза не нужно, чтобы «Бог играл в кости», как писал Альберт Эйнштейн, добавляя в уравнения, описывающую реальность, случайные члены. Оказалось, что объекты, поведение которых невозможно предсказать на достаточно большие времена могут быть очень простыми. Было показано, что чувствительность системы к начальным данным может вести к хаосу. Это явление получило название эффекта бабочки, который связан с тем, что малые причины приводят к большим следствиям. Так, например, несмотря на совершенствование в течение десятков лет математических моделей, использование сверхмощных компьютеров, разработки новых численных методов и совершенствовании систем наземного, воздушного и космического мониторинга за состоянием погоды, не удалось разработать эффективную методику ее среднесрочного (на 2-3 недели вперед) прогноза для конкретных географических точек земной поверхности. Горизонт прогноза для состояния океана эксперты оценивают в месяц. В этих случаях «взмах бабочки» в конкретной точке в некоторый момент времени может привести к ураганам и изменению погоды в огромном регионе. Экономические прогнозы, опирающиеся на представления о хаосе, стали бурно развивающейся областью деятельности [5].
Одно из новых направлений исследования сложных динамических систем связано с предсказанием редких катастрофических событий. Оказалось, что самые разные катастрофические события могут развиваться по одним законам, например фондовый рынок и тектонический разлом – незадолго перед катастрофой. В обоих случаях есть быстрый катастрофический рост, на который накладываются ускоряющиеся колебания. Это так называемые режимы с обострением, когда одна или несколько величин, характеризующих систему, за конечное время вырастает до бесконечности. Проведенный анализ статистики катастроф XX века показал, что статистика землетрясений, наводнений, ураганов, биржевых крахов, ущерба от утечки конфиденциальной информации и многих других подчиняется степенным распределениям из которых следует, что вероятность появления катастрофических событий значительно выше, чем это следует из нормального закона, который до недавнего времени использовался при анализе рисков катастрофически неблагоприятных исходов. Из нормального закона следует, например, что вероятность отклонения случайной величины от среднего значения более чем на три среднеквадратичных отклонений составляет менее 0,001, а параметры катастрофического события практически невозможны. Однако фактическая частота появления катастрофических событий показывает, что это не так.
Еще одно направление исследований в области прогнозирования динамических систем связано с искусственными нейронными сетями, которые оказались эффективным инструментом обработки информации.
Достаточно подробный анализ алгоритмов и перспектив использования методов нелинейной динамики для оценки временных рядов приведен в [5].
6.4 Классификация математических моделей систем
Рассмотрим теперь проблему моделирования систем применительно к инженерной практике. В настоящее время здесь установилась классификация видов моделирования по характеру допущений о моделируемом объекте и виду используемого математического аппарата. Эта классификация относится к широкому кругу систем, в том числе и к информационным системам.
Следуя классификации Б.Я. Советова [7,8], рассмотрим следующие виды моделей систем.
1) Непрерывно-детерминированные модели (D-схемы). В этом виде моделей в качестве рабочего аппарата используются дифференциальные уравнения – либо обыкновенные, либо дифференциальные уравнения в частных производных. Процессы, происходящие в моделях данного типа, зависят от непрерывного (физического) времени. При этом все параметры уравнений предполагаются точно известными (детерминированными). Это же относится и к воздействиям,влияющим на систему – они также рассматриваются в виде детерминированных сигналов. Наибольшее распространение этот вид моделей получил в теоретической механике, механике сплошных сред, а также в классической теории автоматического управления.
2) Дискретно-детерминированные модели (F – схемы).В этом виде моделей время предполагается дискретным, т.е. все процессы, происходящие в системе, привязываются к последовательности временных шагов, или тактов. Функции состояния системы определяются на множестве моментов дискретного времени. Рабочим аппаратом таких моделей служат разностные уравнения, определяющие состояние системы в определенный момент времени на основе информации о состояниях в предыдущие моменты дискретного времени. Все параметры системы и все входные воздействия, как и в предыдущем случае, предполагаются детерминированными. К этому классу моделей относят также важный класс схем, определяемых как конечные автоматы (F –автоматы). Конечный автомат при своей работе по определенному закону переходит из одного состояния в другое в зависимости от внешних воздействий и собственного состояния в данный и предыдущие моменты дискретного времени. Поведение таких систем изучает теория конечных автоматов. Наиболее широкая область применения теории конечных автоматов – моделирование цифровых и других дискретных устройств. К данному виду моделей можно отнести также сети Петри.
3) Дискретно-стохастические модели (P – схемы).В моделях данного вида, в отличие от предыдущего вида, переход из одного состояния в другое происходит случайным образом. При этом уже невозможно говорить о том, в каком конкретно состоянии находится система, речь идет о распределении вероятностей пребывания в том или ином состоянии. К таким моделям относят вероятностные автоматы (P – автоматы). Вероятностный конечный автомат при своей работе с определенной вероятностью переходит из одного состояния в другое в зависимости от внешних воздействий и собственного состояния в данный и предыдущие моменты дискретного времени. Примером таких автоматов могут служить модели, построенные на формализмов цепей Маркова, а также сети Петри с вероятностным поведением.
4) Непрерывно-стохастические модели (Q – модели). Модели данного типа рассматриваются в непрерывном времени, но их поведение носит случайный характер. Наиболее известный класс таких моделей представляют собой системы массового обслуживания (Q – схемы). Как правило, рассматриваются случайные потоки заявок, поступающие в систему, их обработка системой. Определяются, например, такие параметры как время обслуживания заявок, длина очереди на обслуживание и другие, связанные с обслуживанием. В терминах систем массового обслуживания удается описывать многие технологические и экономические процессы, системы передачи данных, компьютерные сети.
5) Сетевые модели (N – схемы). Такие модели используются для описания сложных систем, состоящих из самостоятельно работающих и взаимодействующих подсистем. Наиболее известными моделями данного вида являются сети Петри различных модификаций. Кроме того, к сетевым моделям можно отнести различные структурные модели, используемые при разработке бизнес-систем такие как IDEFX и DFD-модели, структурные модели стандарта ARIS и ряд других.
6) Комбинированные модели (A – схемы) реализуют комбинированный подход к формальному описанию систем, включающий все ранее рассмотренные виды моделей. A – схема должна одновременно выполнять несколько функций: являться адекватным математическим описанием объекта моделирования, служить основанием для построения алгоритмов и программ при машинной реализации модели, производить численные расчеты и, желательно, аналитические исследования поведения моделируемой системы. Современные системы моделирования, как правило, реализуют комбинированный подход. Они позволяют в визуальном режиме описывать моделируемый объект в любой удобной для исследователя форме (непрерывной, дискретной, детерминированной, случайной, сетевой), а затем производить в интерактивном режиме сложные исследования его поведения, получая информацию в наглядной графической, табличной или текстовой форме. Примерами систем моделирования, реализующих комбинированный подход являются MatLab, MVS, AnyLogic.
Рассмотрим более подробно эти классы моделей применительно к информационным системам.
6.5 Модели классов D и F- детерминированные динамические системы
Динамической системой (в общем случае управляемой) называют структуру (рисунок 6.2), формально задаваемую четверкой множеств и двумя функциями: 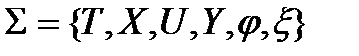 и определяемую следующими аксиомами [16].
и определяемую следующими аксиомами [16].
А. Заданы:
- множество моментов времени 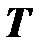 ;
;
- множество состояний 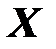 ;
;
- множество значений входных (управляющих) воздействий 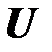 ;
;
- множество выходных величин 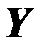 .
.
Б. Множество 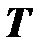 есть некоторое упорядоченное подмножество множества вещественных чисел (т.е. определено направление времени). Величина
есть некоторое упорядоченное подмножество множества вещественных чисел (т.е. определено направление времени). Величина 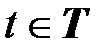 называется моментом времени.
называется моментом времени.
 .
.

Рисунок 6.2. Структура динамической системы
В. Множество 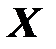 состоит из векторов
состоит из векторов 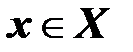 , которые называются векторами состояния или фазовых переменных.
, которые называются векторами состояния или фазовых переменных.
Г. Множество 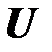 состоит из векторов
состоит из векторов 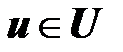 , называемых векторами управляющих воздействий, или векторами управления.
, называемых векторами управляющих воздействий, или векторами управления.
Д. Множество 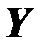 состоит из векторов
состоит из векторов 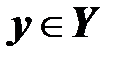 , называемых векторами выходных величин или наблюдений.
, называемых векторами выходных величин или наблюдений.
Е. Существует переходная функция состояния
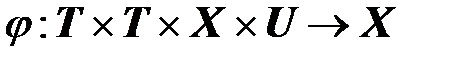 ,
,
значениями которой служат состояния
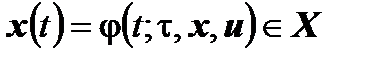 ,
,
в которых оказывается система å в момент времени 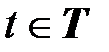 , если в начальный момент времени
, если в начальный момент времени 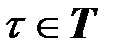 она была в начальном состоянии
она была в начальном состоянии 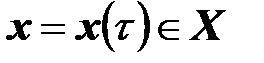 и если на нее действовало входное воздействие
и если на нее действовало входное воздействие 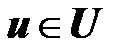 .Функция
.Функция 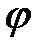 обладает следующими свойствами.
обладает следующими свойствами.
1. Направление времени. Функция 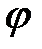 определена для всех
определена для всех 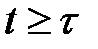 и не обязательно определена для всех
и не обязательно определена для всех 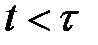 .
.
2. Согласованность. Равенство 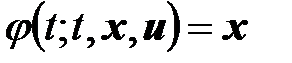 выполняется при любых
выполняется при любых 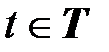 , любых
, любых 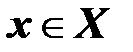 и любых
и любых 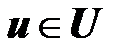 .
.
3. Полугрупповое свойство. Для любых 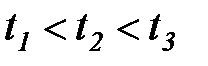 и любых
и любых 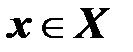 и
и 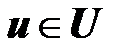 имеем
имеем
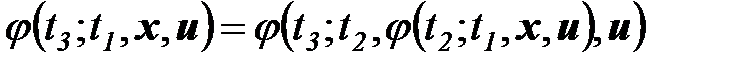 .
.
4. Причинность. Если 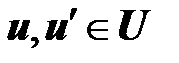 и
и 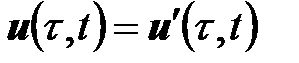 , то
, то 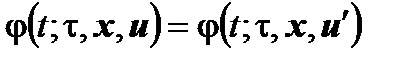 .
.
Ж. Задано выходное отображение 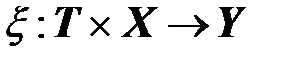 , определяющее выходные величины
, определяющее выходные величины 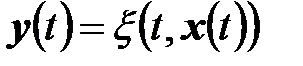 .
.
Пару 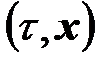 , где
, где 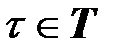 ,
, 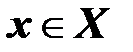 называют событием (или фазой) системы
называют событием (или фазой) системы 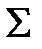 , а множество
, а множество 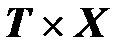 - пространством событий (или фазовым пространством) системы
- пространством событий (или фазовым пространством) системы 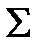 . Переходную функцию состояния
. Переходную функцию состояния 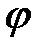 (или ее график в пространстве событий) называют фазовой траекторией. Говорят также, что входное воздействие или управление
(или ее график в пространстве событий) называют фазовой траекторией. Говорят также, что входное воздействие или управление  переводит состояние
переводит состояние 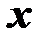 (или событие
(или событие  ) в событие
) в событие 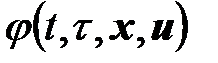 .
.
Приведенное определение является весьма широким. Ему соответствуют, например, конечные автоматы, цепи Маркова и т.д.
В дальнейшем мы ограничимся более узкими классами динамических систем, которые обычно рассматриваются в теории систем.
Дата добавления: 2016-06-13; просмотров: 1642;
