Характеристики временных рядов
Общим для всех моделей временных рядов является предположение о том, что текущее значение процессов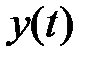 
в значительной степени предопределено его предысторией. Математически это допущение может быть выражено следующим общим уравнением:
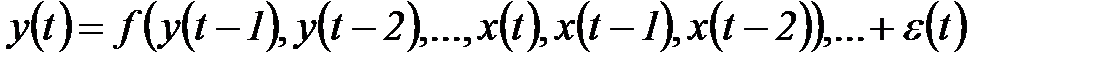(5.68)
где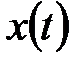 
- внешний фактор, действующий на рассматриваемый процесс, 
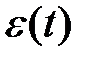– ошибка модели в момент времени t.
Переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными.
Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно разделить на три группы:
1) Факторы, формирующие тенденцию (трендовую компоненту) временного ряда. Эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель, но в совокупности они формируют его возрастающую (убывающую) тенденцию (рисунок 5.13). Тренд – это очищенная от случайностей основная тенденция временного ряда.
2) Факторы, формирующие циклическую компоненту временного ряда (циклические или периодические колебания ряда) (рисунок 5.14). Примером колебаний сезонного характера являются цены на сельскохозяйственную продукцию или спрос на зимнюю одежду. Известен также 11-летний цикл солнечной активности, который влияет на многие процессы на Земле. Для исследования экономических систем важно выделение конъюктурных факторов, связанных с большими экономическими циклами, а также с фазой бизнес цикла, в которой находится экономика. Эти факторы можно выявить при наличии больших массивов данных за длительный промежуток времени.
3) Случайные факторы, формирующие случайную компоненту временного ряда (рисунок 5.15), которые определяются внешним влиянием или недостаточной изученностью процесса.
Рисунок 5.13 – Возрастающая тенденция временного ряда (трендовая компонента временного ряда)
Рисунок 5.14 – Сезонная компонента временного ряда
Рисунок 5.15 – Случайная компонента временного ряда
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен суммой перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда.
Корреляционная зависимость между последовательными уровнями временного ряда называется автокорреляцией уровней ряда.
Основными статистическими характеристиками временного ряда являются математическое ожидание
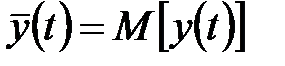, (5.69)
дисперсия
(5.70)
и автокорреляционная функция временного ряда
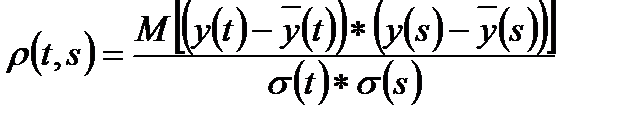, (5.71)
где 
, 
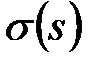– средние квадратические отклонения. В приведенных формулах и далее черта над переменной означает осреднение по времени.
Из (5.71) следует, что автокорреляционная функция временного ряда - это функция двух переменных, равная коэффициенту корреляции между двумя значениями временного ряда y(t) и y(s).
Оценками автокорреляционной функции являются коэффициенты автокорреляции
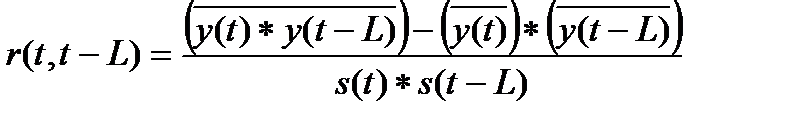, (5.72)
где
,
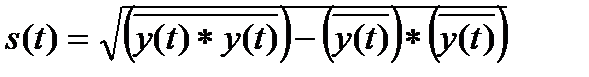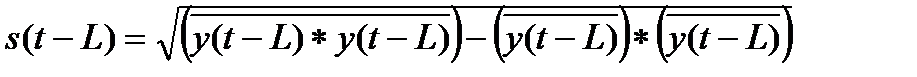, (5.73)
, 
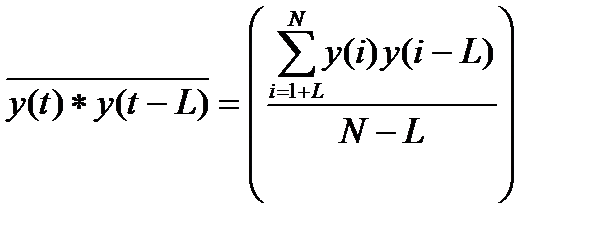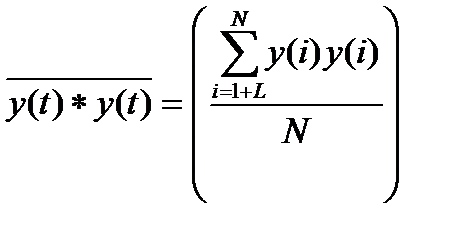, (5.74)
, 
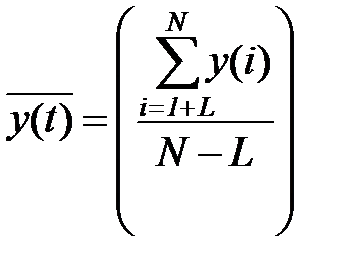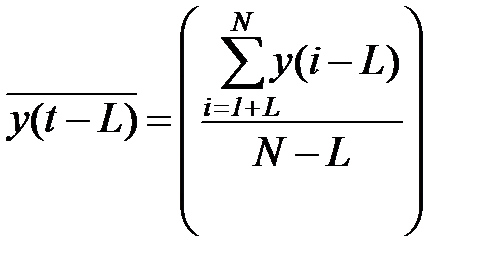. (5.75)
Здесь 
- длина ряда. График зависимости значений коэффициентов автокорреляции от величины лага L называется коррелограммой.
Если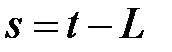 
, то сдвиг по времени L называется лагом, который определяет порядок коэффициента автокорреляции. Если L=1, то имеем коэффициент автокорреляции 1-го порядка 
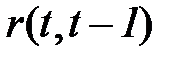если L=2, то коэффициент автокорреляции 2-го порядка 
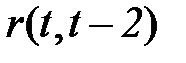и т.д.
Напомним два важных свойства коэффициента автокорреляции:
1) Он характеризует тесноту линейной связи текущего и предыдущего уровней. Поэтому по коэффициенту автокорреляции можно судить о наличии только линейной тенденции.
2) По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Многие временные ряды экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Различают стационарные и нестационарные временные ряды.
В стационарных временных рядах все характеристики не меняются со временем. В частности, математическое ожидание и дисперсия являются постоянными величинами, а автокорреляционная функция зависит только от разности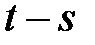 
.
В настоящее время разработано большое количество методов анализа и прогнозирования временных рядов, которые программно реализованы и включены в математические пакеты. Ниже рассмотрен один из таких методов, сравнительно простой, но достаточно эффективный [24].
Дата добавления: 2016-06-13; просмотров: 2360;