Стадии и этапы создания АС 4 страница

Из передатчика сигналы поступают в канал передачи или среду, в качестве которой могут выступать пара проводов (телефонная связь), коаксиальный кабель (телевизионная передача), оптический кабель, полоса радиочастот (радио передача/прием), луч света видимого или инфракрасного диапазона или лазерный сигнал. В канале связи (среде), как правило, на сигнал действуют помехи, которые искажают его, поэтому прием — восстановление информации осуществляется в условиях шумов (помех). Шумы при радиоприеме — это искровые разряды в атмосфере, промышленные помехи, искрение контактов в транспортных средствах и др. Работе радиолокационных систем мешают помехи, специально создаваемые противником.

В приемнике сообщение восстанавливается, здесь обычно выполняются операции, обратные тем, которые имеют место в передатчике: усиление сигнала, демодуляция, декодирование. С выхода приемника расшифрованное сообщение поступает адресату.

Рассмотренную модель системы связи можно принять как некоторую системную модель наравне с моделями массового обслуживания, автоматического управления и прочими для решения задач управления.

Анализ общей структурной схемы связи показывает, что классическая теория информации в основном состоит из двух частей: теории преобразования сообщений и сигналов, основную долю в которой составляют вопросы кодирования и декодирования, и собственно теории передачи сообщений и сигналов без шумов и с шумами в канале связи.

Носителем сообщения или информации является сигнал. Следует различать физические (реальные) сигналы и их математические модели. Разновидностей реальных сигналов много, однако, большинство из них описывается сравнительно небольшим количеством математических моделей. Очевидно, что при таком описании допускается какая-то погрешность, которая в одних случаях (моделях) существенно, а в других несущественно искажает природу реального сигнала. Сложность сведения реального сигнала к его математической модели состоит в том, что для этого нет достаточно общих правил. Кроме того, в зависимости от задачи уровень детализации может изменяться.

Математические модели в зависимости от природы сигналов делятся на детерминированные и случайные. Чаще всего в теории информации, как и в кибернетике, используются случайные модели сигналов.

Эти сигналы могут быть стационарными и нестационарными. Свойства стационарного сигнала не изменяются во времени.

Различают также марковские и немарковские сигналы. Марковским сигналом называется случайный сигнал, поведение которого после некоторого момента 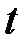не зависит от поведения в предшествующие моменты времени (подробнее об этом сказано в главе 6).

Сигналы могут быть непрерывными и дискретными. Дискретные сигналы различаются по тактовой частоте и амплитуде, и в соответствии с этим их называют квантованными по времени или амплитуде. При квантовании по времени берутся значения непрерывного сигнала в дискретные моменты времени. В общем случае интервалы между моментами времени могут не быть равными.

В качестве примера сигнала, квантованного по амплитуде и времени, рассмотрим сигнал, закодированный двоичным кодом, который часто применяется для передачи сообщения на расстояние (рисунок 5.2) при цифровой системе передачи данных.

На рисунке 5.2, а представлен непрерывный сигнал, на рисунке 5.2,б — тот же сигнал, но квантованный по времени, на рисунке 5.2, в каждое из этих дискретных значений сигнала представлено в виде последовательности импульсов, закодированных двоичным кодом. Каждая кодовая комбинация отделяется от другого маркерным импульсом. На практике при передаче сообщений и сигналов используются протоколы и интерфейсы, предусмотренные стандартами открытых систем OSI, которые были рассмотрены в третьей главе.

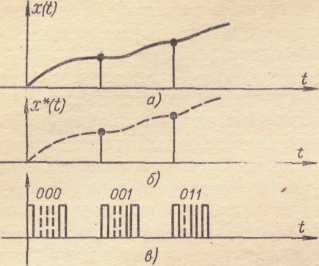
Рисунок 5.2 Дискретный по времени сигнал при цифровой системе передачи данных: а – исходный сигнал, б – квантованный сигнал, в – двоичные коды квантованного сигнала.

Преобразование непрерывного сигнала 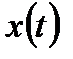в дискретный 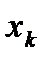может быть представлено как результат работы квантователя, который замыкает цепь сигнала через время 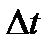на короткий период 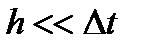(рисунок 5.3).

Рисунок 5.3 Квантователь сигнала

5.2 Детерминированные модели сигналов

Рассмотрим некоторые простейшие детерминированные модели сигналов, которые будут использованы в дальнейшем [16].

1. Ступенчатая и единичная функции.

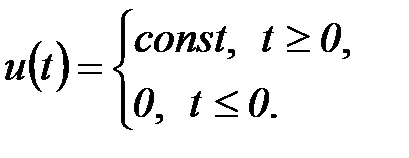
Если 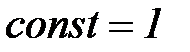, функцию называют единичной и обозначают следующим образом:

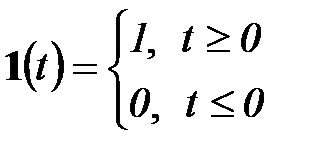(5.1)

График единичной функции показан на рисунке 4.4

Рисунок 5.4 – Единичная ступенчатая функция

Ступенчатая функция представляет собой модель сигнала при его мгновенном изменении (например, при включении системы). В точке 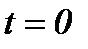функция 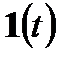имеет разрыв первого рода.

2. Функция Хаара, которая определяется соотношением [11]

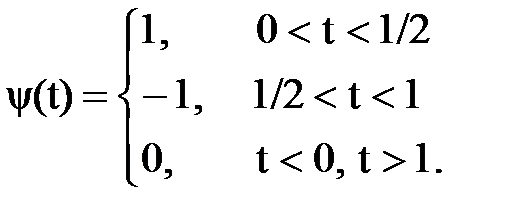(5.2)

Эта функция представляет собой «прямоугольную волну» и может быть получена комбинацией единичных ступенчатых функций со сдвигом по времени и изменением знака.

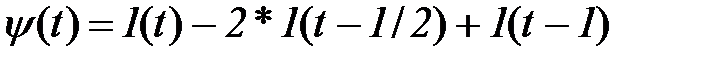
На основе функции (4.2) может быть построено семейство функций Хаара. Это осуществляется изменением масштаба времени и приведением функции к единичной норме:

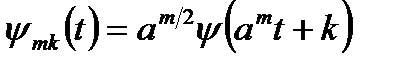, (5.3)

при этом , .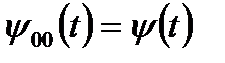

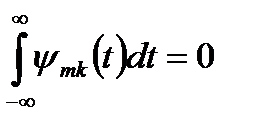Легко проверить, что при а=2, m=0,1,2, ... , k=0,1,2, … две любые функции вида (5.3), полученные с помощью масштабных преобразований и переносов, имеют единичную норму и ортогональны, т.е. их скалярное произведение удовлетворяют условию

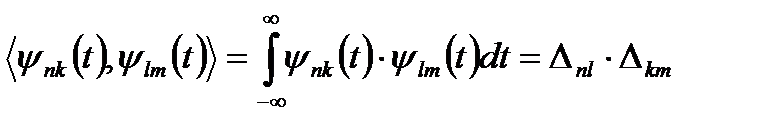(5.4)

Здесь 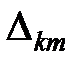- символ Кронекера: · .

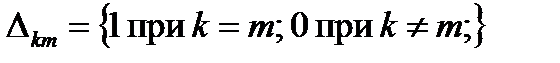Таким образом, функции Хаара образуют ортонормированный базис, что позволяет раскладывать произвольные функции времени с ограниченной нормой по компонентам этого базиса.

График нескольких функций Хаара приведен на рисунке 5.5.

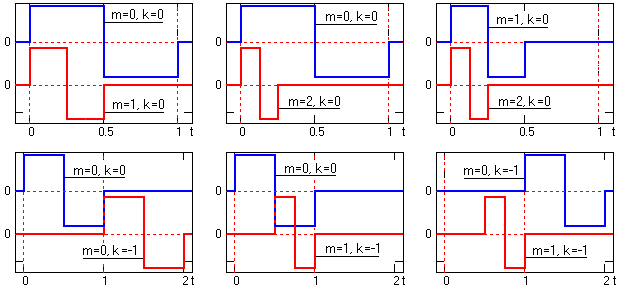
Рисунок 5.5. Функции Хаара при различных k и m

2. Дельта-функция 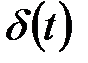. Это так называемая обобщенная функция, или функция Дирака, формально представляющая собой производную от единичной функции

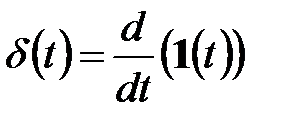(5.5)

с дополнительным условием

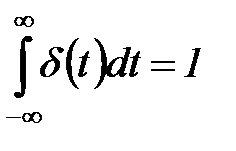. (5.6)

Поскольку 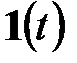- разрывная функция, то 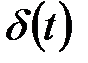с точки зрения классической математики не существует, но она может рассматриваться как производная 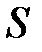‑образной функции при ее стремлении к единичной.

С физической точки зрения 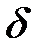-функция - это модель импульса единичной мощности и бесконечно малой длительности. В силу (5.6) его амплитуда должна стремиться к бесконечности, что физически невозможно. Таким образом 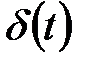- это лишь теоретическая модель сигнала.

Важным свойством 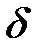-функции является следующее. Если некоторый сигнал 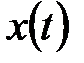ограничен на всей оси времени, то

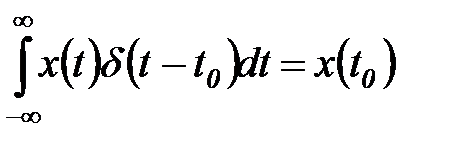, (5.7)

т.е. дельта-функция «вырезает» значение произвольного сигнала 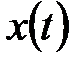в точке 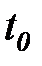. Пользуясь этим свойством, можно представить любую функцию 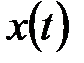в виде последовательности дельта – функций, умноженных на соответствующее значение 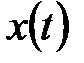. Для этого заменим 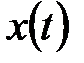ступенчатой ломаной с основанием ступени 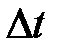. Получаем

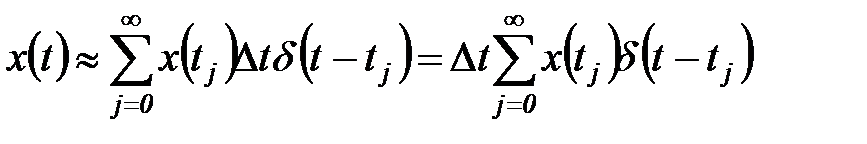. (5.8)

Таким образом, квантованный сигнал можно представить как последовательность 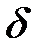-функций, умноженных на значение функции в соответствующей точке (см. рисунок 5.2 б)

3. Гармоническая (синусоидальная) функция может быть представлена в комплексной форме

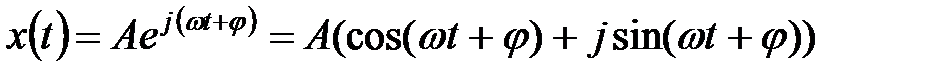. (5.9)

Здесь 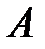– амплитуда сигнала, 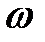– его частота, 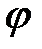– сдвиг по фазе. В некоторых случаях достаточно рассматривать только действительную или только мнимую часть этой функции.

Как известно, множество гармонических функций при 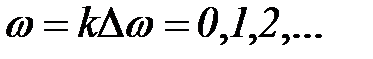образует ортонормированный базис, по которому могут быть разложены функции с ограниченной нормой. Такое разложение называется рядом Фурье и будет более подробно рассмотрено в разделе 5.3.6.

5.3 Преобразование сигналов

Для анализа сигналов в информационных системах широко используются операционное исчисление и частотные методы. Интегральные преобразования позволяют перейти от изучения сигналов как функций времени к их изображениям ‑ функциям комплексных переменных. Такой переход часто упрощает анализ динамических систем.

5.3.1 Преобразование Лапласа

Напомним основные факты, связанные с этим преобразованием [16].

Пусть задан сигнал, представляющий собой скалярную функцию времени 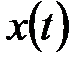, обладающую следующим свойствам:

1) 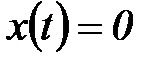при ;

2) существует 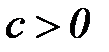, такое, что интеграл

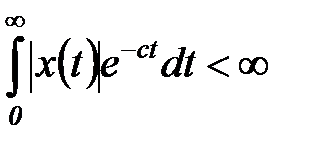. (5.10)

условие (5.10) накладывает ограничения на скорость роста функции 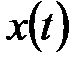- она не должна расти быстрее экспоненты .

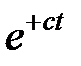Преобразованием (оператором) Лапласа называют интеграл, определяющий по заданной функции времени 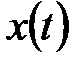функцию комплексного аргумента 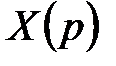, где 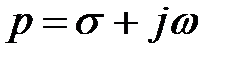, причем :

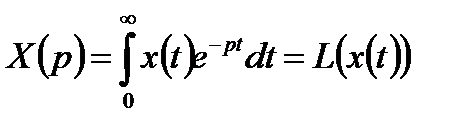. (5.11)

Символ 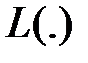называют оператором преобразования Лапласа и используют для краткого обозначения преобразования (5.11).

Обратным преобразованием Лапласа называют интеграл, определяющий функцию 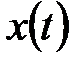по :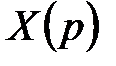

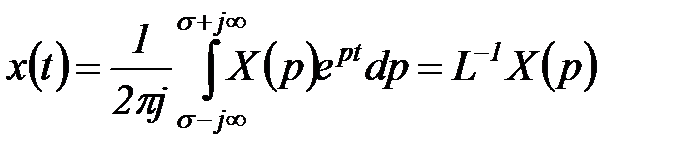. (5.12)

Символ 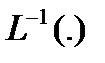означает оператор обратного преобразования Лапласа.

Напомним следующие свойства преобразования Лапласа.

1. Свойство суперпозиции.

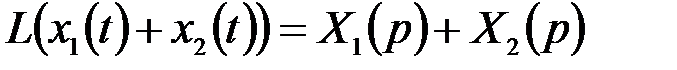, (5.13)

где , .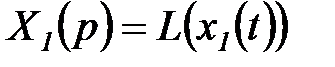

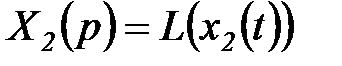2. Свойство линейности.

Если 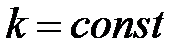, то

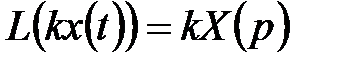. (5.14)

3. смещение в вещественной области (теорема запаздывания). Если 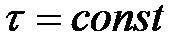, то

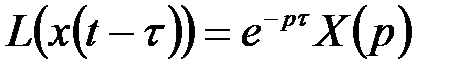. (5.15)

4. смещение в комплексной области.

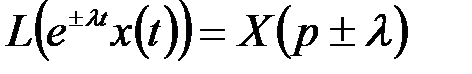. (5.16)

5. умножение изображений (теорема свертки).

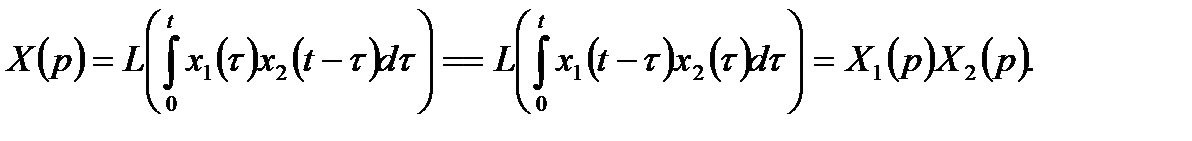(5.17)

6. подобие (изменение масштаба).

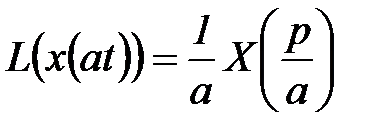, (5.18)

где .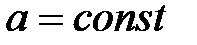

7. Изображение производной функции:

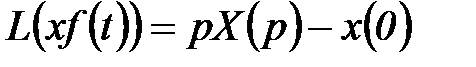. (5.19)

Изображение n - й производной

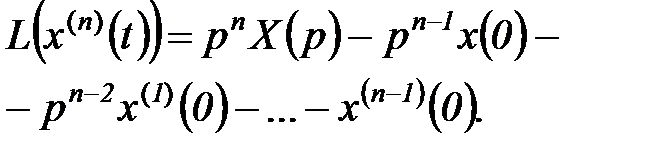(5.20)

8. Изображение интеграла функции по времени

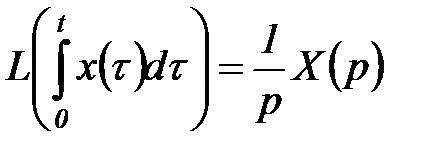. (5.21)

Приведем преобразование Лапласа рассмотренных ранее функций. Непосредственно из определения преобразования Лапласа и его свойств следуют формулы:

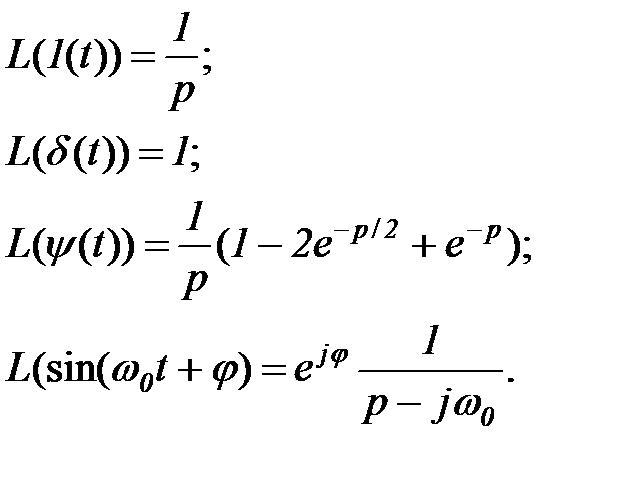
Преобразование Лапласа широко применяется при анализе динамики систем, этот математический аппарат рассмотрен в шестой главе.

5.3.2 Преобразование Фурье

Если в (5.10) функция 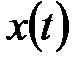такова, что 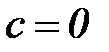, т.е. 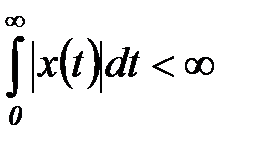, то в формуле (5.11) можно положить 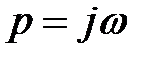, и мы получим формулы, дающие преобразование Фурье.

Прямое преобразование Фурье:

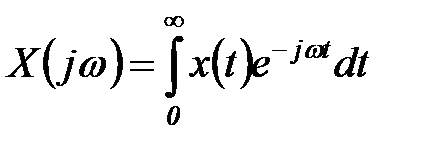(5.22)

и обратное преобразование Фурье:

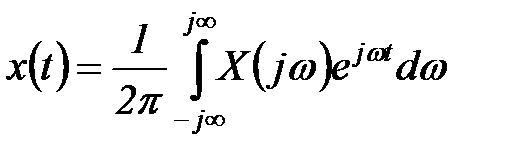. (5.23)

С преобразованием Фурье и его разновидностями мы подробнее ознакомимся в данном курсе при анализе случайных процессов, при изучении частотных характеристик линейных динамических систем. Символ 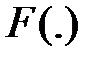называют оператором преобразования Фурье.

Приведем преобразование Фурье рассмотренных выше функций. Формально Фурье-преобразование функции получается из ее преобразования Лапласа путем замены 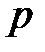на :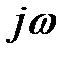

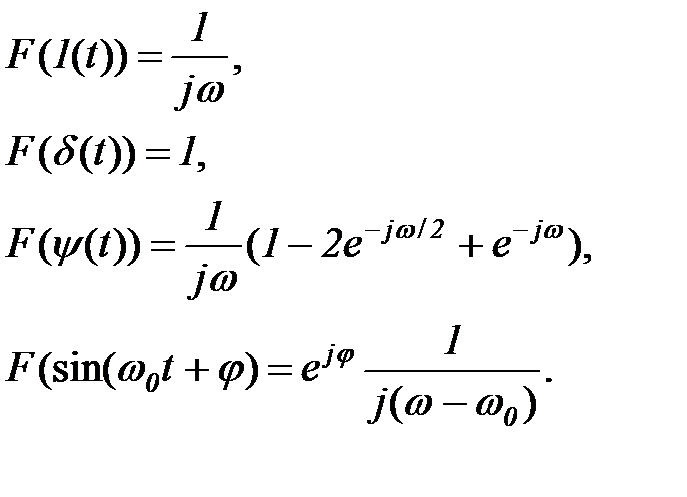
5.3.3 z-преобразование

Рассмотрим функцию дискретного времени 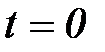, 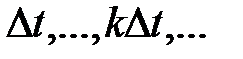Представим такую функцию 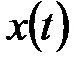как последовательность импульсов, каждый из которых является 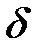-функцией, сдвинутой относительно начала отсчета на 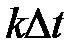и умноженной на :

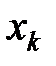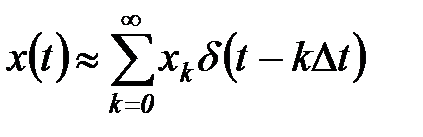, (5.24)

где .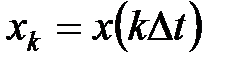

Применим к (5.24) преобразование Лапласа. В силу теоремы запаздывания (свойство 3) и, учитывая изображение 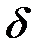-функции, имеем:

,

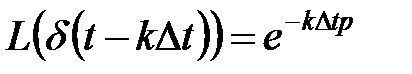откуда

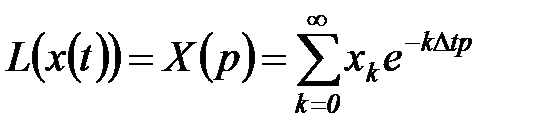. (5.25)

Введем новую переменную 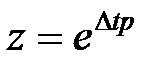, тогда изображение (5.25) примет вид

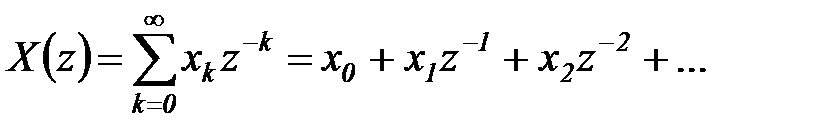(5.26)

Выражение (5.26) называется 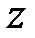-преобразованием функции дискретного аргумента. Бесконечный ряд (5.26) сходится, если все 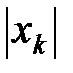ограничены и если 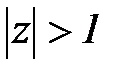(соответственно ).

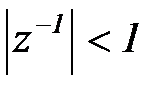Обратное 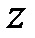-преобразование производится на основе формул (5.25) и (5.26).

Если 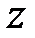-преобразование функции 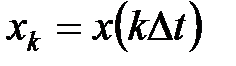представлено в виде ряда

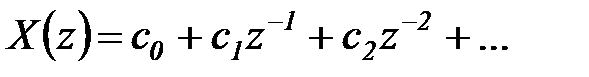
то сама функция 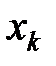имеет вид

, , ,...

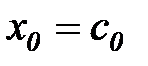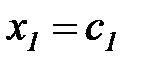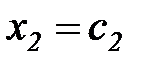Символически операторы прямого и обратного 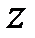-преобразования обозначают соответственно 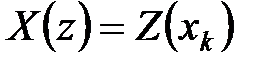и .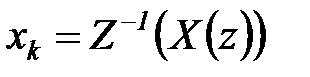

Перечислим некоторые свойства 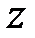-преобразования, которые понадобятся в дальнейшем.

1. Свойство линейности и суперпозиции:

.

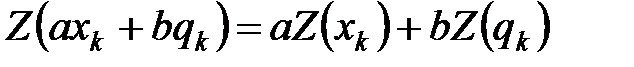2. Сдвиг по времени вправо:

, .

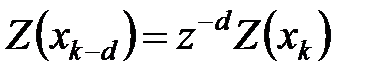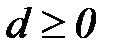3. Изменение масштаба переменной:

.

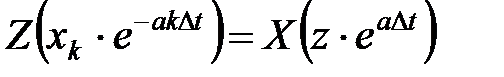5.3 Модели случайных сигналов

5.3.1 Характеристики случайных сигналов

Случайным называется сигнал, описываемый случайными функциями. Случайной функцией некоторой независимой переменной t называется такая функция x(t), значение которой при любом заданном t является случайной величиной [9,10].

Поскольку процессы информационных систем протекают во времени, постольку мы будем рассматривать случайные функции одного аргумента — времени t.

На практике встречаются случайные функции нескольких аргументов. Например, температура в какой-либо точке земной поверхности является случайной функцией не только времени, но и координат рассматриваемой точки.

Понятие случайной величины неразрывно связано с множеством опытов. Поэтому и понятие случайной функции также связано с множеством опытов.

Функция, получаемая в результате каждого отдельного опыта, является определенной, неслучайной. Эта функция называется конкретной реализацией случайной функции. Случайная функция представляет собой совокупность всех реализаций.

Пусть, например, имеется большое число полностью идентичных приборов, напряжения шумов которых записываются в течение некоторого интервала времени Т.

Запись напряжения шума на выходе каждого данного прибора в интервале Т является конкретной реализацией, а вся совокупность записей характеризует случайную функцию (рисунок 5.5). Случайная функция x(t) при данном t=t_l по определению есть случайная величина x(t₁) и часто называется сечением случайной функции.

Сечение x(t₁) случайной функции, как и любая другая случайная величина, характеризуется распределением вероятностей.

Рисунок 5.5 Реализации стационарного случайного процесса

Функция распределения вероятностей (интегральное распределение вероятностей)

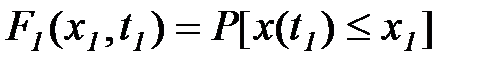(5.27)

выражает вероятность того, что случайная функция x(t) в момент времени t = t₁ меньше заданной величины x₁ . Плотность вероятности 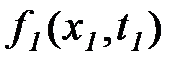есть производная от интегрального распределения вероятности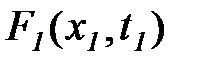

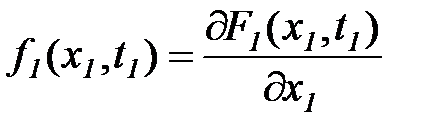. (5.28)

Величина 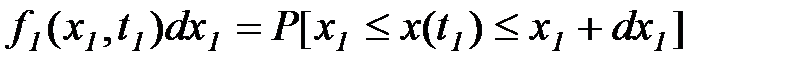выражает вероятность того, что случайная функция x(t) в момент времени t = t₁ имеет значение в интервале от 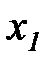до x₁+dx₁.

Функции распределения вероятностей 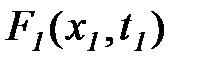, 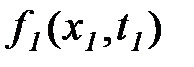называются одномерными, так как они относятся только к одному (вообще говоря, произвольному) сечению случайной функции.

Математическим ожиданием или средним (по множеству) значением случайной функции называется такая неслучайная функция 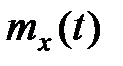, которая при любом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции. Из этого определения и понятия математического ожидания случайной величины следует:

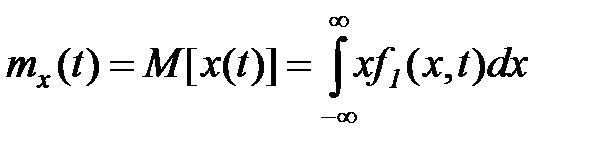(5.29)

Разность 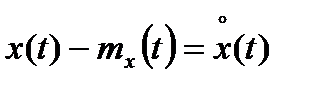называется центрированной случайной функцией. Математическое ожидание центрированной случайной функции равно нулю:

.

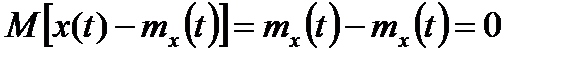Дисперсией случайной функции называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

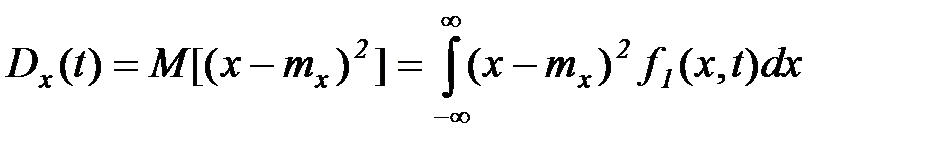(5.30)

Эта функция в любой момент времени t равна дисперсии соответствующего сечения случайной величины.

Распределение вероятностей служит исчерпывающей характеристикой случайной величины. Однако для случайной функции одномерное распределение вероятностей не является достаточной характеристикой. Действительно, одномерное распределение вероятностей и, тем более, такие производные характеристики, как математическое ожидание и дисперсия, ни в коей мере не характеризуют протекание случайного процесса во времени. Так, например, для всех процессов, в которых распределение вероятности не зависит от времени, изменение масштаба по оси времени никак не отражается на указанных характеристиках. Между тем, воздействие на динамическую систему каждой из реализаций возмущающей силы зависит от изменения этой силы во времени.

Определенную характеристику временных свойств случайной функции дают многомерные распределения вероятностей. Так, двухмерное распределение вероятностей

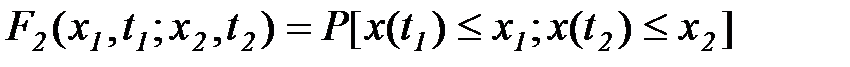(5.31)

относится к двум произвольным сечениям x(t₁), x(t₂) случайной функции и выражает вероятность того, что в момент времени t₁ случайная функция меньше 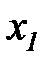, а в момент 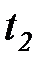— меньше .

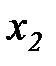Можно рассматривать также n-мерное распределение вероятностей, охватывающее п сечений. Эти понятия используются обычно не столько для практических вычислений, сколько для теоретических построений и определений.

Практически для характеристики временной структуры центрированной случайной функции используется математическое ожидание произведения двух сечений этой функции

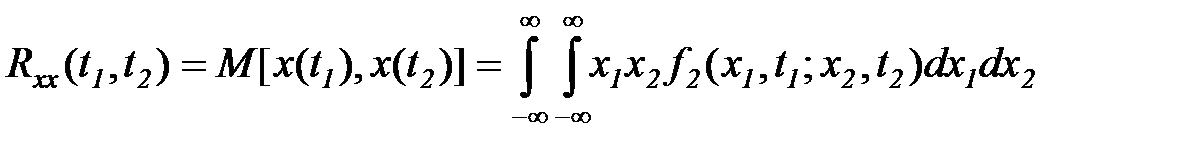. (5.32)

Эта функция называется корреляционной или автокорреляционной и играет важную роль в теории случайных процессов. Из определения корреляционной функции ясно, что она симметрична относительно переменных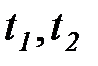

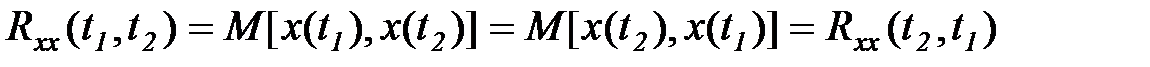. (5.33)

Если 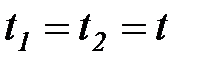, то

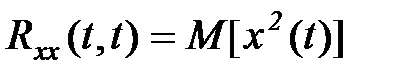. (5.34)

Таким образом, корреляционная функция, отнесенная к одному и тому же сечению, равна среднему значению квадрата случайной функции. Если случайная функция x(t) центрирована, то, в соответствии с (5.30), 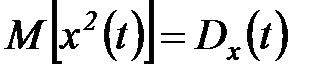и корреляционная функция при 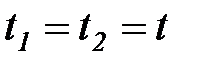равна дисперсии случайной функции.

Во многих случаях на одну и ту же систему действует несколько случайных возмущающих сил, независимых или взаимосвязанных. Для характеристики статистической взаимосвязи случайных функций используются совместное распределение вероятностей и взаимная корреляционная функция.

Если имеются две случайные функции x(t), y(t), то совместная функция распределения вероятностей