Стадии и этапы создания АС 3 страница
По коду Бодо, применявшемуся в буквопечатающих аппаратах, каждой букве соответствует сигнал из пяти импульсов одинаковой длительности и формы. Пример кодировки символов также приведен в таблице. Этот код равномерен, так как на каждый символ требуется одинаковое время.
При передаче сигналов, определяемых некоторыми случайными процессами, возможна дискретизация сигнала по времени и амплитуде, а возможна передача коэффициентов разложения сигнала по некоторым базисным функциям (гармоническим, вейвлет-функциям и другим). В любом случае на принимающей стороне необходимо восстанавливать сигнал в исходной форме
Таблица 4.2
Примеры кодов Морзе и Бодо
| А | Б | В | Г | Д | |
| Код Морзе | |||||
| Код Бодо |
Следует различать способ кодирования и способ модуляции сигнала или сообщения.
Так, рассмотренные коды Морзе и Бодо — двоичные, т.е. имеют двоичное основание: сообщения передаются с помощью посылки сигнала (тока) или его отсутствия. Могут быть троичные коды, когда используются посылки положительного и отрицательного знака и отсутствие посылки, пятеричные и т.д. Единичная посылка сигнала может быть в виде напряжения постоянного или переменного тока (радиоимпульса). Наконец, можно передавать тире тремя импульсами, а точку — отсутствием импульсов.
В первом случае имеет место модулированный сигнал постоянного тока, во втором сигнал переменного тока, модулированный прямоугольным напряжением, так называемый радиоимпульс (если частота наполнения лежит в диапазоне радиочастот). Наконец, в последнем случае имеет место кодо-импульсная модуляция. Помимо рассмотренных, могут быть и другие виды модуляции.
По физической природе сигналы могут быть электрические, акустические, механические, радиолокационные и пр. В данном курсе не исследуются ни физическая природа сигналов, ни виды модуляции.
4.3 Оптимальный код Шеннона – Фено
Рассмотрим кратко понятие об оптимальном кодировании символьных сообщений.
Для построения оптимального кода Шеннона — Фено все символы алфавита располагаются в порядке убывания вероятности их появления. Символу, встречающемуся чаще всего, присваивается наиболее короткая комбинация. В английском языке чаще всего встречается буква 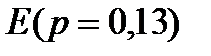 (смотри таблицу 4.1).Этой букве отведена самая короткая кодовая комбинация — точка. В русском языке наиболее повторима буква О
(смотри таблицу 4.1).Этой букве отведена самая короткая кодовая комбинация — точка. В русском языке наиболее повторима буква О 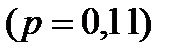 , но ей отведена далеко не самая короткая кодовая комбинация — три тире. В этом смысле для русского языка принятая система кодирования в азбуке Морзе не является оптимальной.
, но ей отведена далеко не самая короткая кодовая комбинация — три тире. В этом смысле для русского языка принятая система кодирования в азбуке Морзе не является оптимальной.
Оптимальным считается код, имеющий минимальную среднюю длину
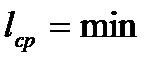 ,
,
причем
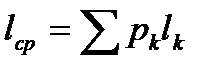 ,
,
где суммирование выполняется по всем символам алфавита; 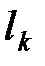 — длина кодовой комбинации, равная числу ее элементов, соответствующая
— длина кодовой комбинации, равная числу ее элементов, соответствующая 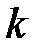 -мусимволу алфавита;
-мусимволу алфавита; 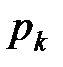 — вероятность появления в сообщениях данного ансамбля
— вероятность появления в сообщениях данного ансамбля 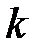 -го символа; при этом
-го символа; при этом
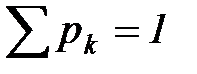 .
.
Здесь будут рассмотрены только двоичные коды, хотя все изложенное справедливо и для других кодов.
Пример.Рассмотрим таблицу 4.3, в которой приведен алфавит, состоящий из шести символов (сообщений).
Таблица 4.3
Формирование оптимальных кодов
| № сообщения | Вероятность | Группы | Подгруппы | Оптимальные коды | |
| 1-го уровня | 2-го уровня | ||||
| 0,3 | I | I | |||
| 0,2 | II | ||||
| 0,15 | II | I | I | ||
| 0,15 | II | ||||
| 0,1 | II | I | |||
| 0,1 | II |
Во втором столбце даны вероятности появления символов, в третьем, четвертом, пятом — разбиение па группы и подгруппы, в шестом— кодовые комбинации, которые строятся так: все символы разбиваются на две группы, чтобы суммарные вероятности в каждой группе были примерно равны.
В нашем примере в первую группу попали два первых символа, во вторую — все остальные. Первой группе присваивается символ 1 в первом слева разряде, второй — 0. Далее процесс повторяется: первая группа разбивается на две подгруппы примерно с одинаковыми суммарными вероятностями и т. д. То же самое делается со второй группой. Процесс деления заканчивается, когда в каждой подгруппе остается по одному символу. Графически этот процесс можно изобразить в виде ветвящегося дерева (графа), представленного на рисунке.
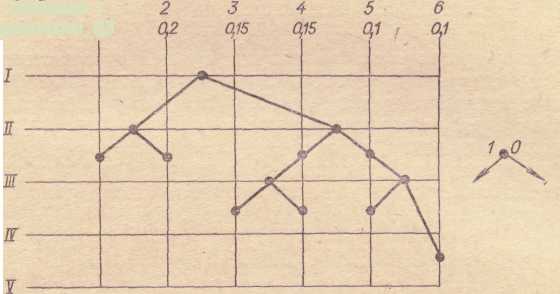
Рисунок 4.1 Дерево построения оптимального кода
4.4 Корректирующие коды
Корректирующие коды применяются для повышения надежности передачи данных. Основная идея построения таких кодов заключается в том, что наряду с кодовой группой, несущей полезную информацию, передаются дополнительные знаки, с помощью которых удается обнаруживать и исправлять ошибки, возникшие при прохождении сообщения. Такая процедура вносит избыточность, снижает эффективность системы передачи, зато повышает ее помехоустойчивость.
В простейшем случае такой код получается добавлением к кодовой комбинации единицы или нуля с тем, чтобы сумма всех единиц была четной. Нечетность суммы будет обозначать наличие ошибки. Поясним этот прием на примере кода Бодо в таблице 4.3. Такой код позволяет обнаружить одиночную ошибку, но не в состоянии ее локализовать и исправить.
Таблица 4.3
Примеры кодов Бодо и дополнительного кода Бодо
| А | Б | В | Г | Д | |
| Код Бодо | |||||
| Дополнительный код Бодо |
Не только обнаружить, но и исправить ошибку можно с помощью более мощных кодов, которые строятся следующим образом.
Пусть для передачи информации требуется 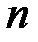 двоичных знаков, тогда общее число комбинаций
двоичных знаков, тогда общее число комбинаций 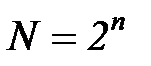 . Каждый из таких кодов отличается один от другого хотя бы одним знаком. Дополним код еще одним знаком, а число полезных кодовых комбинаций оставим неизменным, тогда
. Каждый из таких кодов отличается один от другого хотя бы одним знаком. Дополним код еще одним знаком, а число полезных кодовых комбинаций оставим неизменным, тогда 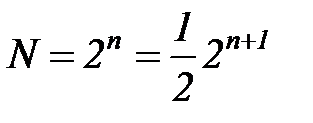 , и можно так подобрать кодовые комбинации, что они будут отличаться двумя знаками. При этом будет использована только половина всех возможных комбинаций от
, и можно так подобрать кодовые комбинации, что они будут отличаться двумя знаками. При этом будет использована только половина всех возможных комбинаций от 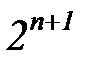 , вторая половина образует запрещенные комбинации: любое появление одиночной ошибки превращает комбинацию в запрещенную, и тем самым ошибка обнаруживается. Дополним теперь код таким количеством знаков, которое даст возможность двум кодовым комбинациям отличаться тремя знаками при неизменном числе
, вторая половина образует запрещенные комбинации: любое появление одиночной ошибки превращает комбинацию в запрещенную, и тем самым ошибка обнаруживается. Дополним теперь код таким количеством знаков, которое даст возможность двум кодовым комбинациям отличаться тремя знаками при неизменном числе 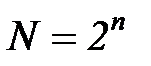 . Такой код позволит не только обнаружить, но и исправить одиночную ошибку. Действительно, если случилась одиночная ошибка в какой-то комбинации, то эта комбинация от других будет отличаться на два знака, а от своей – на один, и ее легко исправить.
. Такой код позволит не только обнаружить, но и исправить одиночную ошибку. Действительно, если случилась одиночная ошибка в какой-то комбинации, то эта комбинация от других будет отличаться на два знака, а от своей – на один, и ее легко исправить.
Определим общее число дополнительных знаков, необходимых для обнаружения и исправления одиночных ошибок. Пусть из общего числа позиций 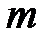 сигнала для передачи полезной информации используется
сигнала для передачи полезной информации используется 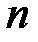 , которое будем считать фиксированным. Остальные
, которое будем считать фиксированным. Остальные 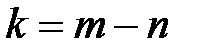 используются в качестве проверочных. Символы, которые ставятся на
используются в качестве проверочных. Символы, которые ставятся на 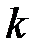 проверочных позициях, определяются при кодировании проверкой на четность каждой из
проверочных позициях, определяются при кодировании проверкой на четность каждой из 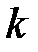 групп информационных символов. При этом на каждой проверочной позиции при кодировании ставится 0 или 1, смотря по тому, какая сумма единиц – четная или нечетная получается при каждой из
групп информационных символов. При этом на каждой проверочной позиции при кодировании ставится 0 или 1, смотря по тому, какая сумма единиц – четная или нечетная получается при каждой из 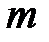 проверок на четность. Сигнал кодируется так, чтобы в результате каждой из
проверок на четность. Сигнал кодируется так, чтобы в результате каждой из 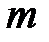 проверок получалось четное число.
проверок получалось четное число.
Построим код, который позволял бы обнаруживать и исправлять одиночную ошибку (против двух ошибок сразу код бессилен).
Пусть принята кодовая комбинация с ошибкой или без нее. Произведем последовательно 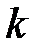 проверок. После каждой проверки запишем 0, если на проверяемых позициях не обнаружено ошибки (сумма единиц четная). Запись справа налево полученной последовательности единиц и нулей дает двоичное число, называемое проверочным. Потребуем, чтобы это число давало номер позиции, на которой произошла ошибка. Отсутствию ошибки будет соответствовать проверочное число, составленное их нулей. Проверочное число должно описывать
проверок. После каждой проверки запишем 0, если на проверяемых позициях не обнаружено ошибки (сумма единиц четная). Запись справа налево полученной последовательности единиц и нулей дает двоичное число, называемое проверочным. Потребуем, чтобы это число давало номер позиции, на которой произошла ошибка. Отсутствию ошибки будет соответствовать проверочное число, составленное их нулей. Проверочное число должно описывать 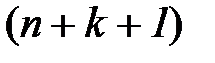 событий. Следовательно, число
событий. Следовательно, число  определяется на основе неравенства
определяется на основе неравенства 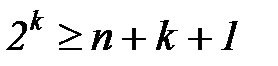 , и поскольку
, и поскольку 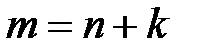 , то
, то 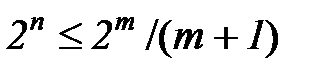 . Это соотношение позволяет определить минимальное
. Это соотношение позволяет определить минимальное 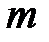 при заданном числе знаков передаваемой полезной информации
при заданном числе знаков передаваемой полезной информации 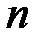 . Например, при
. Например, при 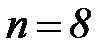 общее число разрядов в сообщении составит
общее число разрядов в сообщении составит 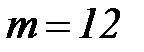 , то есть потребуется число дополнительных разрядов
, то есть потребуется число дополнительных разрядов 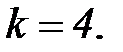
Для некоторых значений 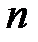 и
и 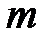 значения
значения 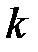 приведены в таблице 4.4.
приведены в таблице 4.4.
Таблица 4.4
Необходимое число дополнительных разрядов для корректирующего кода
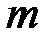
| ||||||||
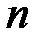
| ||||||||
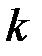
|
Определим теперь позиции, которые надлежит проверить в каждой из 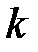 проверок. Если ошибок нет, то на всех проверяемых позициях будет 0, если в низшем разряде числа стоит 1, то это значит, что в результате первой проверки обнаружена ошибка.
проверок. Если ошибок нет, то на всех проверяемых позициях будет 0, если в низшем разряде числа стоит 1, то это значит, что в результате первой проверки обнаружена ошибка.
При первой проверке проверяются те номера позиций, двоичные представления которых имеют в самом правом разряде единицы:
1 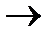 1, 3
1, 3  11, 5
11, 5  101, 7
101, 7  111, 9
111, 9  1001 и т.д.
1001 и т.д.
Таким образом, первая проверка охватывает позиции 1, 3, 5, 7, 9.
Для второй проверки выбирают такие позиции, двоичные представления которых имеют единицу во втором с конца разряде:
2 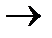 10, 3
10, 3 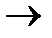 11, 6
11, 6 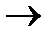 110, 7
110, 7 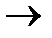 111, 10
111, 10 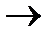 1010.
1010.
Аналогично проводим третью проверку в третьем с конца разряде:
4 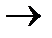 100, 5
100, 5 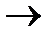 101, 6
101, 6 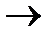 110, 7
110, 7 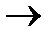 111, 12
111, 12 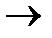 1100, 13
1100, 13 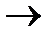 1101.
1101.
Такой выбор проверяемых позиций дает возможность определить позиции, в которых произошла одиночная ошибка. Напомним, что при каждой проверке сумма единиц должна быть четной.
Пример 1. Пусть произошла ошибка в одной из позиций первой проверки, тогда в проверочном числе в низшем (правом) разряде появится единица. Дальнейшую расшифровку проверочного числа дает вторая проверка: если среди всех позиций второй проверки ошибок нет, то появится нуль. Если на третьей позиции произошла ошибка, нарушившая четность как в первой, так и во второй проверке, то после двух проверок в двух низших разрядах появятся единицы. В третьей и следующих проверках третья позиция уже отсутствует. Таким образом, в нашем примере проверочное число равно 0011=3, что и дает номер позиции, на которой произошла ошибка. Аналогично можно убедиться, что любая одиночная ошибка на любой позиции может быть устранена проверками, дающими проверочное число, равное номеру позиции, на которой произошла ошибка.
Определим теперь, какие позиции следует использовать для проверочных символов. Если выбрать для проверки позиции 1, 2. 4, 8,… , то при каждой проверке будет участвовать хотя бы одна из этих позиций, и это позволит независимо от знаков передаваемого числа получит при каждой проверке четное число единиц. Соответствующие проверяемые разряды, как было показано выше, образуют таблицу 4.5.
Таблица 4.5
Проверяемые разряды
| Номер проверки | Проверяемые разряды |
| 1, 3, 5, 7, 9, 11, 13, … | |
| 2, 3, 6, 7, 10, 11, 14, … | |
| 4, 5, 6, 7. 12, 13, … |
Пример 2. Построим код Хемминга для 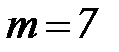 ,
, 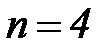 ,
, 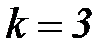 . Для передачи проверочных символов будут использоваться разряды 1, 2, 4 (эти разряды выделены заливкой), остальные разряды будут использоваться для передачи информации, в них разместим двоичные коды чисел от 0 до 15. В результате получим кодовые комбинации, приведенные в таблице 3.6. Как видно, построенный код допускает передачу 16 сообщений, при этом
. Для передачи проверочных символов будут использоваться разряды 1, 2, 4 (эти разряды выделены заливкой), остальные разряды будут использоваться для передачи информации, в них разместим двоичные коды чисел от 0 до 15. В результате получим кодовые комбинации, приведенные в таблице 3.6. Как видно, построенный код допускает передачу 16 сообщений, при этом 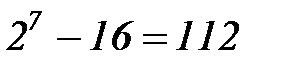 комбинаций не используются.
комбинаций не используются.
Пример 3.Проиллюстрируем работу построенного кода. Рассмотрим комбинацию 0110011, которая соответствует числу 11 в таблице 4.6. Допустим, сто при передаче произошла ошибка, и символ в пятой позиции сменился на противоположный. Получилась комбинация 0110111. Определим ошибку по изложенной выше методике.
Первая проверка (сумма разрядов 1, 3, 5, 7 нечетная) дает 1.
Вторая проверка (сумма разрядов 2, 3, 6, 7 четная) дает 0
Третья проверка (сумма разрядов 4, 5, 6, 7 нечетная) дает 1
В итоге получаем проверочное число (101)2 = 5. Следовательно, на пятой позиции произошла ошибка, и знак в этой позиции необходимо заменить на обратный (1 на 0). В результате восстановится правильная комбинация 0110011.
Корректирующую способность кода можно повышать и дальше: строить коды для обнаружения 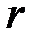 - кратной и исправления
- кратной и исправления 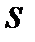 - кратной ошибок. Конечно, при этом будет расти количество дополнительных знаков и общая длина кодовой комбинации при неизменном размере полезного кода. Эти вопросы рассматриваются в теории помехоустойчивого кодирования [9,10 ].
- кратной ошибок. Конечно, при этом будет расти количество дополнительных знаков и общая длина кодовой комбинации при неизменном размере полезного кода. Эти вопросы рассматриваются в теории помехоустойчивого кодирования [9,10 ].
Таблица 4.6
Код Хэмминга для передачи 4-х разрядных двоичных слов
с обнаружением и исправлением одиночной ошибки
| Разряды передаваемого кода | Десятичное представление передаваемого сообщения | ||||||
4.5 Современные системы кодирования текстовых символов
В заключение раздела рассмотрим современные кодировки текстовых данных в информационных системах. В силу того, что вычислительные ресурсы современных компьютеров достаточно велики, в большинстве приложений отпала необходимость использовать экономные методы кодирования при хранении данных.
Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это сложно сделать из-за противоречий между символами национальных алфавитов, а также противоречий корпоративного характера. Во второй главе мы рассмотрели общие вопросы стандартизации в области информационных технологий. Создание систем кодирования, несомненно, является одной из важнейших задач в процессе стандартизации области ИТ.
Для английского языка, захватившего де-факто нишу международного средства общения, противоречия уже сняты. Институт стандартизации США (ANSI — American National Standard Institute) ввел в действие систему кодирования ASCII (American Standard Code for Information Interchange — стандартный код информационного обмена США).
В системе ASCII для кодирования каждого символа отведено 8 двоичных разрядов – 1 байт, что дает возможность закодировать 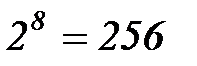 различных символов. Существуют две таблицы кодирования — базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.
различных символов. Существуют две таблицы кодирования — базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.
Первые 32 кода базовой таблицы, начиная с нулевого, отданы производителям аппаратных средств (в первую очередь производителям компьютеров и печатающих устройств). В этой области размещаются так называемые управляющие коды, которым не соответствуют никакие символы языков, и, соответственно, эти коды не выводятся ни на экран, ни на устройства печати, но ими можно управлять тем, как производится вывод прочих данных и осуществлять контроль и корректировку данных.
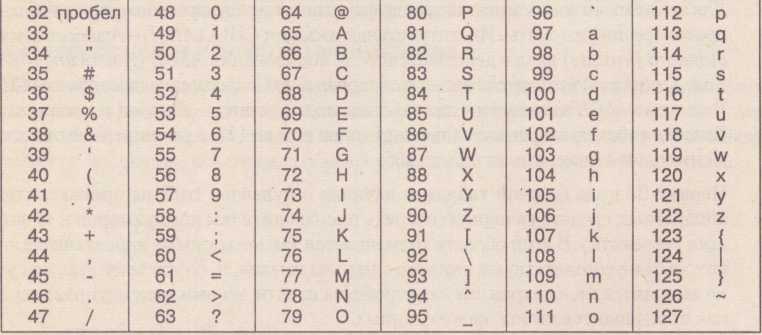
Начиная с кода 32 по код 127 размещены коды символов английского алфавита, знаков препинания, цифр, арифметических действий и некоторых вспомогательных символов. Базовая таблица кодировки ASCII приведена в таблице 4.7.
Таблица4.7
Фрагмент таблицы ASCII – кодов
Аналогичные системы кодирования текстовых данных были разработаны и в других странах. В СССР в этой области действовала система кодирования КОИ-7 (код обмена информацией, семизначный). Однако поддержка производителей оборудования и программ вывела американский код ASCII на уровень международного стандарта, и национальным системам кодирования пришлось «отступить» во вторую, расширенную часть системы кодирования, определяющую значения кодов со 128 по 255. Другая распространенная кодировка носит название КОИ-8 (код обмена информацией, восьмизначный) — ее происхождение относится ко временам действия Совета Экономической Взаимопомощи государств Восточной Европы. Сегодня кодировка КОИ-8 имеет широкое распространение в компьютерных сетях на территории России и в российском секторе Интернета.
Отсутствие единого стандарта в этой области привело к множественности одновременно действующих кодировок. Только в России можно указать три действующих стандарта кодировки и еще два устаревших.
Так, например, кодировка символов русского языка, известная как кодировка Windows-1251, была введена «извне» — компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение. Эта кодировка используется на большинстве локальных компьютеров, работающих на платформе Windows.
Международный стандарт, в котором предусмотрена кодировка символов русского алфавита, носит название кодировки ISO (International Standard Organization — Международный институт стандартизации). На практике данная кодировка используется редко.
Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). В то же время, очевидно, что если, например, кодировать символы не восьмиразрядными двоичными числами, а числами с большим количеством разрядов, то и диапазон возможных значений кодов станет намного больше. Такая система, основанная на 16-разрядном (2-байтовом) кодировании символов, получила название универсальной — UNICODE. Шестнадцать разрядов позволяют обеспечить уникальные коды для 216 = 65 536 различных символов — этого поля достаточно для размещения в одной таблице символов большинства языков планеты, включая иероглифы.
Несмотря на тривиальную очевидность такого подхода, простой механический переход на данную систему долгое время сдерживался из-за недостаточных ресурсов средств вычислительной техники (в системе кодирования UNICODE все текстовые документы автоматически становятся вдвое длиннее). Во второй половине 90-х годов технические средства достигли необходимого уровня обеспеченности ресурсами, и сегодня мы наблюдаем постепенный перевод документов и программных средств на универсальную систему кодирования.
Для индивидуальных пользователей это еще больше добавило забот по согласованию документов, выполненных в разных системах кодирования, с программными средствами, но это надо понимать как трудности переходного периода.
Глава 5 Обработка сигналов
5.1 Основные понятия: информация и сигнал
В данной главе мы приступаем к описанию информационных процессов, которые осуществляются в информационных системах. Информационные процессы – это процессы получения, передачи, преобразования, хранения, защиты информации. Часть упомянутых процессов рассматривается в других учебных курсах, например, в специальном курсе по информационной безопасности и защите информации.
В данном курсе мы остановимся на общих вопросах, связанных с понятиями информации, обработки сигналов и кодирования [9,10].
Понятие информации - одна из основных категорий рассматриваемой нами теории информационных процессов и систем.
Как уже отмечалось, определения информации, удовлетворяющего общую теорию систем, пока не существует. То понятие информации, которое было рассмотрено в первой главе, носит общефилософский характер. В системном анализе обычно используется определение информации, заимствованное из теории связи и опирающееся на понятие сигнала. Основная его особенность состоит в абстрагировании от смыслового содержания информации, использовании ее количественной меры. Однако для разрешения большинства задач теории систем необходимо оперировать именно количественными характеристиками смыслового или семантического содержания информации.
Следует заметить, что в ряде случаев классическое понятие количества информации бывает полезно при изучении процессов управления. Именно отвлечение от смыслового содержания информации позволяет получать обобщенные характеристики по загрузке каналов связи, памяти ЭВМ, каналов преобразования информации в системах управления и т. д. Теория информации во многом ориентирована на анализ и оценку характеристик сигналов. Поэтому мы кратко рассмотрим теорию сигналов, их анализа и преобразования.
Теория информации имеет дело с определенной моделью передачи и преобразования сигналов.
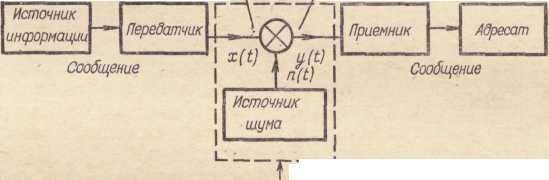
На рисунке 5.1 представлена типичная структурная схема передачи сигналов, используемая в теории связи. Объясняя ее, попутно введем необходимые для теории информационных процессов понятия.
Система связи начинается с источника информации, создающего сообщение или их последовательность для передачи по линии связи. Сообщениями могут быть все виды информационных ресурсов, рассмотренные в первой главе.
Сообщения поступают на передатчик, который перерабатывает их в физические сигналы в соответствии с особенностями данного канала связи. В простейшем случае (при телефонной связи) акустические волны человеческого голоса преобразуются в электрический ток. При радиоприеме эти низкочастотные сигналы наполняются радиочастотой, усиливаются по мощности и пр., а при радиорелейной передаче человеческого голоса необходима специальная система импульсного кодирования.
Переданный сигнал, Принятый сигнал
Канал (среда)
Рисунок 5.1. Общая структурная схема передачи сигналов.
В общем случае передающее устройство имеет преобразователь (микрофон), кодирующее устройство, модулятор, передатчик, выходные устройства передатчика (антенну).
Дата добавления: 2016-06-13; просмотров: 1025;
