Стадии и этапы создания АС 5 страница

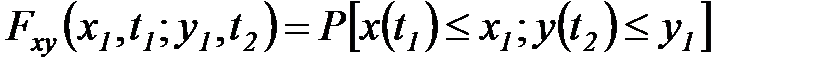(5.35)

выражает вероятность того, что момент времени t = t_l значение x(t₁) меньше y. Совместная плотность вероятностей равна

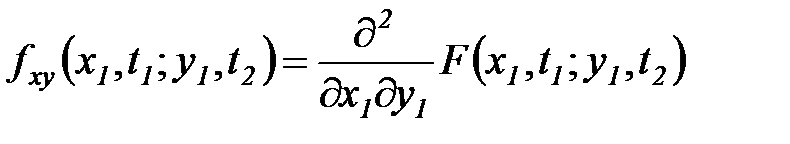. (5.36)

Взаимной корреляционной функцией двух центрированных случайных функций х, у называется математическое ожидание произведения сечений этих функций

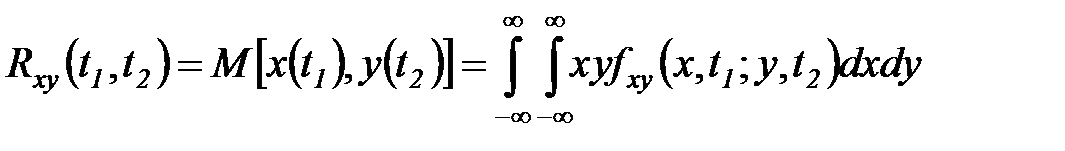. (5.37)

5.3.2 Стационарные и нестационарные случайные процессы

При рассмотрении различных случайных процессов выделяют группу процессов, статистические характеристики которых не изменяются при сдвиге во времени. Эти процессы и соответствующие им случайные функции называются стационарными.

Рисунок 5.6. Пример реализаций нестационарного случайного процесса

Все случайные процессы и соответствующие им функции, не обладающие свойством инвариантности статистических характеристик при временных сдвигах, именуются нестационарными. Рассматривая множество реализаций напряжения шума на выходах приборов, представленное на рисунке 5.2, можно предполагать, что в данном случае налицо стационарный случайный процесс. Сдвиг во времени на интервал Т каждой из реализаций здесь не меняет статистических характеристик (распределений вероятностей, дисперсий, корреляционной функции ит. п.).

Иное положение имеет место для случайного процесса, реализации которого изображены на рисунке 5.6. Здесь перенос во времени каждой из реализаций существенно меняет статистические характеристики случайной функции. Таким образом, данный процесс является нестационарным.

Исследование систем, случайные процессы вкоторых стационарны, значительно проще исследования нестационарных процессов. С другой стороны, процессы во многих системах могут приближенно рассматриваться как стационарные случайные процессы. Это обусловливает большое прикладное значение теории стационарных случайных процессов.

По определению стационарной случайной функции ее корреляционная функция должна удовлетворять соотношению

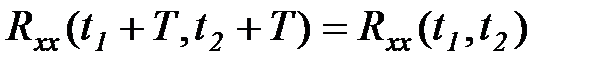. (5.38)

Полагая 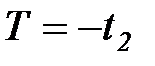, получаем

(5.39)

Таким образом, корреляционная функция стационарного случайного процесса зависит только от разности времени соответствующих сечений и ее удобно обозначать так:

, где .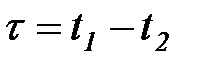

Кроме того, согласно определению корреляционной функции,

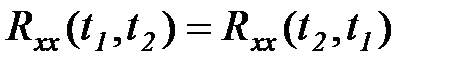, поэтому для стационарного процесса получаем:

,

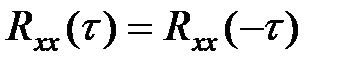т.е. корреляционная функция нестационарного случайного процесса есть четная функция τ.

Рисунок 5.7. Реализация случайных функций:
а- при быстром убывании корреляционной функции;
б- при относительно пологой корреляционной функции

Как уже указывалось, корреляционная функция играет важную роль в теории случайных процессов, и желательно показать физический смысл этой функции для некоторых конкретных примеров.

Корреляционная функция характеризует статистическую связь последующих и предыдущих значений случайной функции. Чем быстрее убывает корреляционная функция при возрастании τ, тем быстрее изменяется случайная функция, тем слабее связь между последующими и предыдущими значениями этой функции. Напротив, если значения корреляционной функции убывают с возрастанием τ медленно, то последующие и предыдущие значения случайной функции имеют сильную связь, реализации случайной функции изменяются относительно медленно. На рисунке 5.7,а приведен пример случайной функции, соответствующий быстрому убыванию 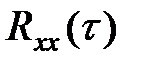. Кривая корреляционной функции имеет здесь острый пик в начале координат. Функция, приведенная на рисунке 5.7,б имеет более плавный характер изменения, и ее корреляционная функция 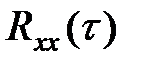уменьшается медленно.

Если ширина пика корреляционной функции бесконечно мала, то мыимеем процесс, называемый белым шумом. Таким образом, белым шумом называется случайный процесс, корреляционная функция которого равна (или пропорциональна δ-функции 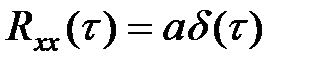, где a=const.

Белый шум — это «чисто» случайный процесс, в нем отсутствует какая-либо связь междупредыдущими и последующими значениями случайной функции.

Белый шум в строгом математическом понятии этого термина физически неосуществим, так как он имеет бесконечную мощность (см. ниже). Однако имеется большое число физических процессов, которые весьма близки к белому шуму.

5.3.3 Свойство эргодичности

Помимо свойства инвариантности статистических характеристик по отношению к сдвигу во времени для стационарных случайных процессов важное значение имеет другое свойство - свойство эквивалентности среднего по времени среднему по множеству. Это свойство носит название эргодичности и формулируется следующим образом.

Пусть имеется случайная функция 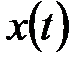. Говорят, что эта функция обладает свойством эргодичности, если для любой из множества реализаций этой функции за исключением, быть может, реализаций с нулевой вероятностью, математическое ожидание произвольной функции 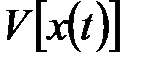равно среднему по времени той же функции

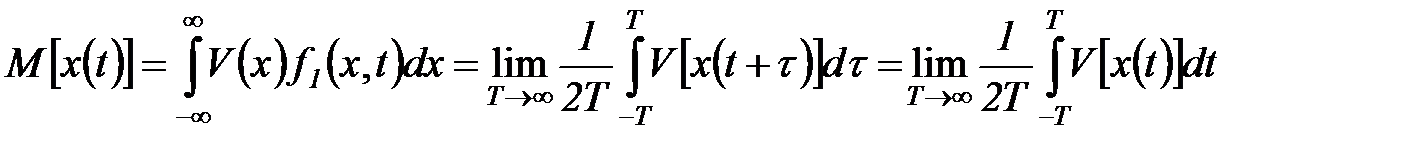. (5.40)

Математическое ожидание есть среднее по множеству. Поэтому кратко эргодическое свойство можноформулировать так: для процесса, обладающего эргодическими свойствами, среднее по множеству реализаций равно среднему по времени для одной реализации.

Практически это означает, что для эргодического стационарного процесса все усредненные характеристики (математические ожидания, дисперсии и т. л.) одинаковы для всех реализаций и эти реализации могут быть заменены одной реализацией, достаточно продолжительной во времени. Для определения характеристик стационарной эргодической случайной функции можно ограничиться одним опытом, осуществленным в течение достаточно большого интервала времени, вместо множества опытов необходимых для определения характеристик неэргодического процесса.

Итак, если некоторый непрерывный сигнал можно рассматривать как эргодический случайный процессx(t) на достаточно длительном интервале времени T, то он может характеризоваться следующими показателями:

математическое ожидание

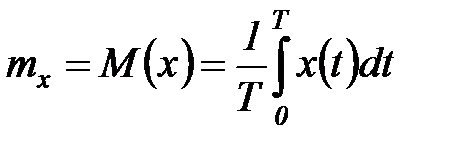; (5.41)

дисперсия

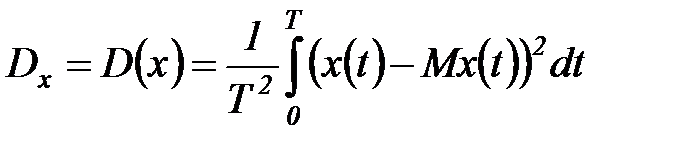; (5.42)

корреляционная функция

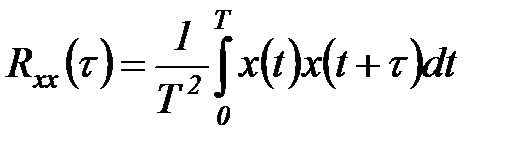. (5.43)

5.3.4 Спектральная плотность стационарного случайного сигнала

Корреляционная функция во многих случаях является достаточной характеристикой для решения задач анализа систем. Однако для стационарных эргодических случайных функций и стационарных систем часто удобнее применять другую характеристику — спектральную плотность мощности или, как часто называют, спектральную плотность.

Существуют два основных определения понятия спектральной плотности мощности.

Первое определение связывает спектральную плотность с корреляционной функцией. Второе определение, рассмотренное ниже в п. 5.4, позволяет оценивать спектральную плотность непосредственно по реализации случайного сигнала.

Спектральной плотностью стационарной случайной функции x(t) называется преобразование Фурье корреляционной функции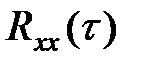

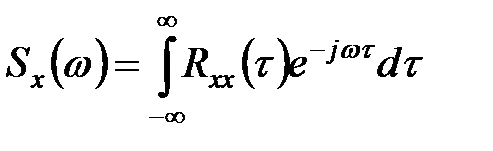. (5.44)

Поскольку корреляционная функция является четной:

,

то спектральная плотность может быть представлена в виде

.

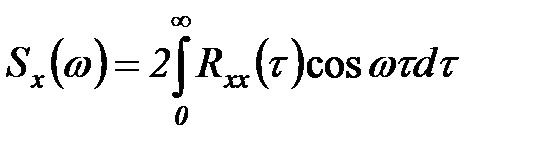Обратное преобразование Фурье выражает корреляционную функцию через спектральную плотность

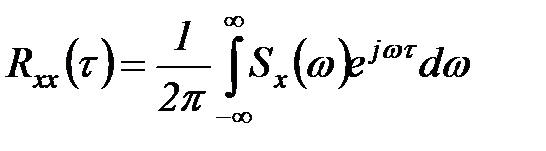. (5.45)

Наименование «спектральная плотность мощности» связана с тем, что размерность функции 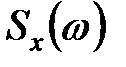для физических случайных процессов обычно (с точностью до размерности электрического или механического сопротивления) совпадает с размерностью мощности.

Спектральная плотность используется как статистическая характеристика не только одной случайной функции, но и взаимной связи нескольких случайных функций.

Если случайные функции 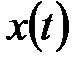, 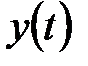стационарны и стационарно связаны, то их взаимной спектральной плотностью называется преобразование Фурье взаимной корреляционной функции

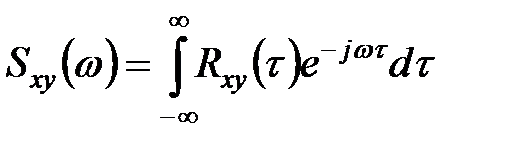. (5.46)

Рисунок 5.8. Характер связи корреляционной функции со спектральной плотностью (кривые1 - a=1, кривые 2 - a=2).

Спектральная плотность и корреляционная функция, связанные между собой прямым и обратным преобразованием Фурье подчиняются следующим закономерностям: чем положе кривая корреляционной функции, тем уже кривая спектральной плотности.

Например, если

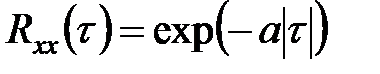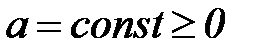, где , то

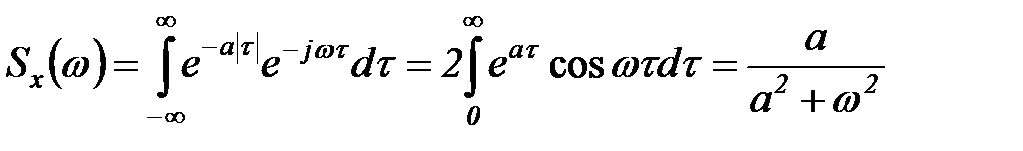. (5.47)

Графики для а=1 и а=5 изображены на рисунке 5.8 (соответственно кривые 1и 2).

Для белого шума корреляционная функция пропорциональна δ-функции

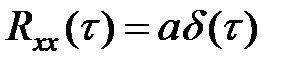, где 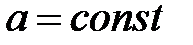и, следовательно,

.

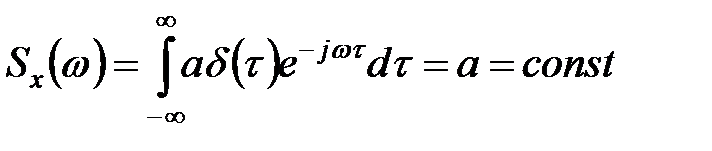Таким образом, спектральная плотность белого шума постоянна на всем бесконечном диапазоне частот, что теоретически соответствует бесконечной мощности сигнала.

Диапазон частот, , в котором спектральная плотность отлична от нуля на некоторую малую величину, называют шириной спектра сигнала, или полосой частот .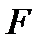

5.3.5 Частотные свойства сигнала (теорема Котельникова)

При получении информации человек с помощью приборов может воспринимать только квантованный по времени и амплитуде сигнал. Но ни человек, ни приборы при определенных условиях не могут отличить сигнал, квантованный по величине, от непрерывного. Дело в том, что как у человека, так и у приборов есть порог чувствительности Δ, из-за которого невозможно отличить два значения сигнала, если они отличаются друг от друга меньше, чем на этот порог. Поэтому квантование по амплитуде производится с шагом .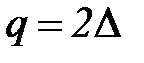

Аналогичная ситуация имеет место при восприятии квантованного по времени сигнала. Если частота поступления значений сигнала превышает некоторую предельную частоту, то невозможно отличить сигнал дискретного времени от сигнала непрерывного времени.

Ниже приведена теорема Котельникова, устанавливающая зависимость между числом дискретных отсчетов на единицу изменения аргумента, необходимым для задания непрерывной функции, и шириной частотного спектра этой функции, доказанная в 1933 В.А. Котельниковым. Эта теорема гласит, что всякая непрерывная функция, спектр которой ограничен полосой частот F, может быть полностью восстановлена по ее дискретным значениям, взятым через интервалы аргумента, равные 1/2F .

Интервал 1/2F есть интервал корреляции, так что общий смысл теоремы Котельникова состоит в том, что для задания непрерывной функции достаточно располагать совокупностью ее некоррелированных значений.

Например, если 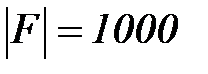гц, то 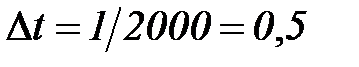мсек.

Аналитически эта теорема доказывается путем представления функции 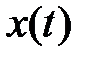,с ограниченным спектром шириной F в виде ряда

.

Для получения такого представления следует спектр функции 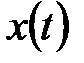разложить в ряд Фурье и почленно подвергнуть обратному преобразованию Фурье.

Для восстановления непрерывной функции по ее дискретным значениям нужно сформировать последовательность бесконечно коротких импульсов, интегральные значения которых пропорциональны дискретным значениям функции (см. формулу 5.8), и пропустить эту последовательность через фильтр нижних частот с граничнойчастотой F. Ввиду сложности выкладок мы доказательство этого утверждения опускаем, оно приведено, например, в [10 ].

Вышеприведенная формулировка теоремы Котельникова относится к функциям с ограниченным спектром, то есть к функциям, спектральная плотность которых тождественно равна нулю вне полосы F. Позднее было показано, что теорема Котельникова применима и к функциям с неограниченным, но достаточно быстро убывающим спектром. В этом случае непрерывная функция восстанавливается по своим дискретным значениям не точно, но с легко оцениваемым приближением. Теоретико-информационное обобщение и уточнение смысла теоремы Котельникова было дано академиком А. Н. Колмогоровым (1956).

Теорема Котельникова играет большую роль в теории связи, где она применяется, в частности, для определения тактовой частоты (частоты следования). При всех видах импульсной передачи эта частота берется не меньше, чем 2F.

5.4 Спектральный анализ случайных сигналов

В разделе 5.3.4 говорилось о вычислении спектра случайного сигнала по его автокорреляционной функции. Другой способ вычисления спектральных характеристик сигналов заключается в применении преобразования Фурье непосредственно самому сигналу.

Фурье-анализ служит основой многих методов, применяющихся в области обработки сигналов: при анализе временных рядов, в технике связи и обработки изображений, при проектировании фильтров в системах управления и в других областях. Преобразование Фурье позволяет сопоставить сигналу, заданному во временной области, его эквивалентное представление в частотной области. Наоборот, если известна частотная характеристика сигнала, то обратное преобразование Фурье позволяет восстановить сигнал во временной области.

До сих пор мы рассматривали стационарные по времени сигналы, у которых все характеристики постоянны во времени и для которых справедлив принцип эргодичности. Однако на практике большинство сигналов, представляющих интерес, нестационарны. Для их анализа необходимы другие методы обработки, которые мы кратко рассмотрим в данном параграфе.

Напомним некоторые математические определения, относящиеся к произвольным сигналам x(t).

В пространстве функций, заданных на конечном интервале (0,T), норма, как наиболее общая числовая характеристика произвольной (в общем случае – комплексной) функции x(t), по определению вычисляется как корень квадратный из скалярного произведения функции. В общем случае, для комплексных функций, квадрат нормы (энергия сигнала) соответствует выражению:

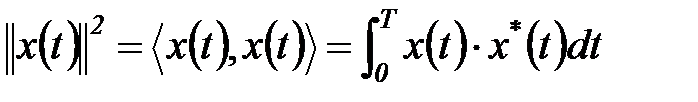, (5.48)

где 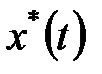– функция, комплексно сопряженная с 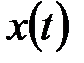. Для действительной функции x^*(t)= x(t).

Если норма функции имеет конечное значение (интеграл сходится), то говорят, что функция принадлежит пространству функций 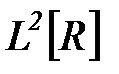, , интегрируемых с квадратом (пространство Гильберта), и, соответственно, имеет конечную энергию. В пространстве Гильберта на основе совокупности ортогональных функций с нулевым скалярным произведением

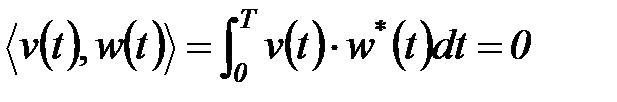
всегда может быть создана система ортонормированных «осей» (базис пространства), при этом любой сигнал, принадлежащий этому пространству, может быть представлен в виде весовой суммы простых составляющих, проекций сигнала на эти «оси» – базисных векторов. Значения проекций определяются скалярными произведениями сигнала с соответствующими функциями базисных «осей».

Базис пространства может быть образован любой ортогональной системой функций. Наибольшее применение в спектральном анализе получила система комплексных экспоненциальных функций (см. раздел 5.1.2). Проекции сигнала на данный базис определяются выражением:

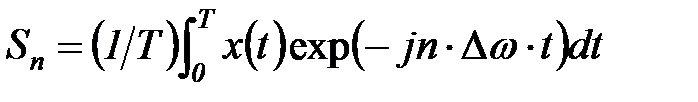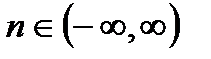, , (5.49)

где 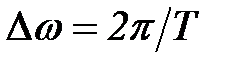– частотный аргумент векторов, 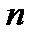- целое число.

При известных выражениях базисных функций сигнал 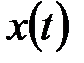однозначно определяется совокупностью коэффициентов S_n и может быть абсолютно точно восстановлен (реконструирован) по этим коэффициентам:

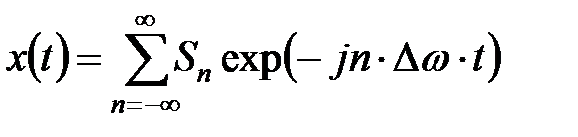. (5.50)

Уравнения (5.49) и (5.50) называют прямым и обратным преобразованием Фурье сигнала 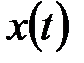. Таким образом, любая функция гильбертова пространства может быть представлена в виде комплексного ряда Фурье (5.50), который называют спектральным представлением сигнала или его Фурье-образом.

На практике ряд Фурье ограничивается определенным количеством членов N. Ограничение числа членов ряда значением N означает аппроксимацию бесконечномерного сигнала N – мерной системой базисных функций спектра сигнала с определенной погрешностью в зависимости от фактического спектра сигнала.

С позиций анализа произвольных сигналов и функций в частотной области и точного восстановления после преобразований можно отметить ряд недостатков разложения сигналов в ряды Фурье, которые привели к появлению оконного преобразования Фурье и стимулировали развитие вейвлетного преобразования. Отметим основные из них.

· Ограниченная информативность анализа нестационарных сигналов и практически полное отсутствие возможностей анализа их особенностей (сингулярностей), т.к. в частотной области происходит «размазывание» особенностей сигналов (разрывов, ступенек, пиков и т.п.) по всему частотному диапазону спектра.

· Гармонические базисные функции разложения не способны в принципе отображать перепады сигналов с бесконечной крутизной типа прямоугольных импульсов, т.к. для этого требуется бесконечно большое число членов ряда. При аппроксимации скачков нелокализованными во времени базисными функциями необходимо, чтобы суперпозиция этих функций не только восстановила скачок, но и уничтожила друг друга за пределами скачка, что делает равнозначимыми все компоненты его спектра. При ограничении числа членов ряда Фурье в окрестностях скачков и разрывов восстановленного сигнала возникают осцилляции (явление Гиббса).

· Преобразованием Фурье отображаются глобальные сведения о частотах исследуемого сигнала, поскольку базисные функции преобразования определены на бесконечном временном интервале. Преобразование Фурье не дает представления о локальных свойствах сигнала при быстрых временных изменения его спектрального состава. Так, например, преобразование Фурье не различает сигнал с суммой двух синусоид, от сигнала с двумя последовательно следующими синусоидами с теми же частотами. Преобразование Фурье в принципе не имеет возможности анализировать частотные характеристики сигнала в произвольные моменты времени.

Частичным выходом из этой ситуации является так называемое оконное преобразование Фурье с движущейся по сигналу оконной функцией, имеющей компактный носитель. Полный временной интервал сигнала, особенно при большой его длительности, разделяется на подинтервалы, и преобразование Фурье выполняется последовательно для каждого окна в отдельности. Тем самым осуществляется переход к частотно-временному (частотно-координатному) представлению сигналов и результатом оконного преобразования является семейство спектров, которым отображается изменение спектра сигнала по интервалам сдвига окна преобразования. Это в какой-то мере позволяет выделять на координатной оси и анализировать особенности нестационарных сигналов. Размер носителя оконной функции 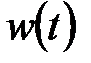обычно устанавливается соизмеримым с интервалом стационарности сигнала. По существу, таким преобразованием один нелокализованный базис разбивается на определенное количество базисов, локализованных в пределах функции 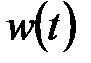, что позволяет представлять результат преобразования в виде функции двух переменных - частоты и временного положения окна. При этом размер стационарности сигнала необходимо знать априори.

Оконное преобразование выполняется в соответствии с выражением:

. (5.51)

Функция 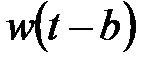представляет собой функцию окна сдвига преобразования по координате t, где параметром b задаются фиксированные значения сдвига. При сдвиге окон с равномерным шагом 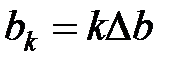в качестве окна преобразования может использоваться как простейшее прямоугольное окно ( 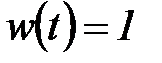в пределах окна и 0 за его границами), так и специальные весовые окна (Бартлетта, Гаусса, Кайзера и пр.), обеспечивающие малые искажения спектра за счет граничных условий вырезки оконных отрезков сигналов и нейтрализующие явление Гиббса. При этом для каждого положения окна на временной оси сигнала вычисляется свой комплексный спектр. Эффективная ширина оконной функции, как правило, сохраняется постоянной по всему интервалу сигнала.

Пример оконного преобразования для нестационарного сигнала при большом уровне шума приведен на рисунке 5.9. По спектру сигнала в целом можно судить о наличии в его составе гармонических колебаний на трех частотах. Оконное преобразование не только подтверждает данное заключение, но и показывает конкретную локальность колебаний по интервалу сигнала и соотношение между амплитудами этих колебаний.

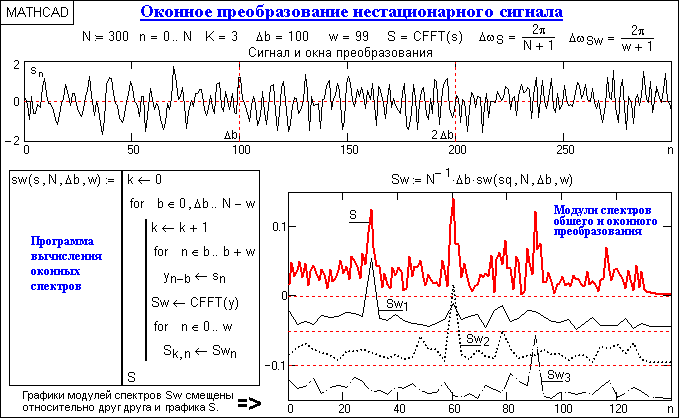
Рисунок 5.9 Пример оконного преобразования нестационарного сигнала

Координатная разрешающая способность оконного преобразования определяется шириной оконной функции и, в силу принципа неопределенности Гейзенберга, обратно пропорциональна частотной разрешающей способности. При ширине оконной функции, равной b, частотная разрешающая способность определяется значением 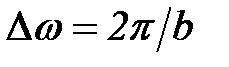. При требуемой величине частотного разрешения 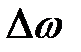соответственно ширина оконной функции должна быть равна 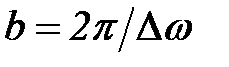. Для оконного преобразования Фурье эти ограничения являются принципиальными. Так, для рисунка 5.9 при размере массива данных N=300 и ширине оконной функции 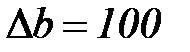частотная разрешающая способность результатов преобразования уменьшается в 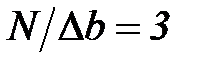раза по сравнению с исходными данными, и графики 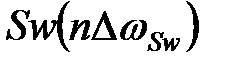по координате n для наглядного сопоставления с графиком 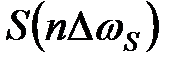построены с шагом по частоте 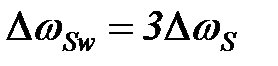, т.е. по точкам .

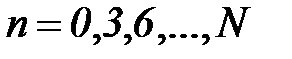5.4.1 Дискретное преобразование Фурье

Разновидностью преобразования Фурье, которое применяется при обработке цифровых сигналов, является дискретное преобразование Фурье, которое оперирует дискретной во времени выборкой периодического сигнала во временной области. Для того чтобы сигнал мог быть представлен в виде суммы синусоид, он должен быть периодическим. Но на практике исходные данные могут содержать только конечное число отсчетов N. Поэтому формально до и после обрабатываемой группы отсчетов следует поместить бесконечное число копий данного сигнала. При этом образуется периодический сигнал.

Уравнение для получения N-точечного дискретного преобразования Фурье (спектра сигнала) выглядит следующим образом:

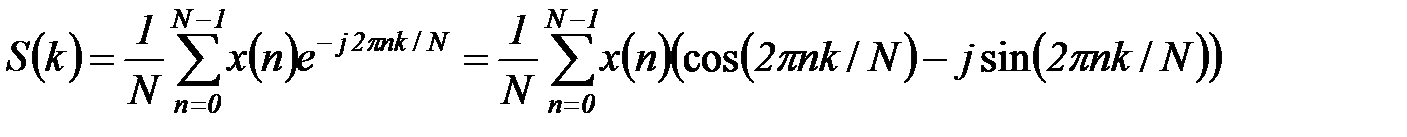. (5.52)

Здесь 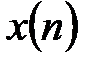- -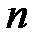ый отсчет дискретного сигнала, 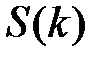- значение частоты в 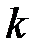-й точке спектра, , .

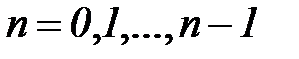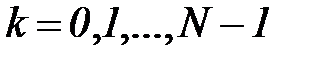Мы видим, что спектр является комплексной функцией. Первая точка спектра 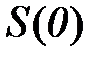является суммой отсчетов входного сигнала, деленной на 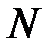, т.е средним значением всех отсчетов, поскольку 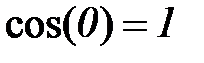, 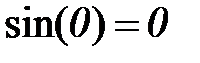. Дальнейшие значения спектра содержат как действительную, так и мнимую части, они получаются умножением значений сигнала на соответствующие значения синуса и косинуса. Часто при вычислении спектра ограничиваются только действительной составляющей.

Для восстановления сигнала по заданной спектральной функции применяется обратное дискретное преобразование Фурье:

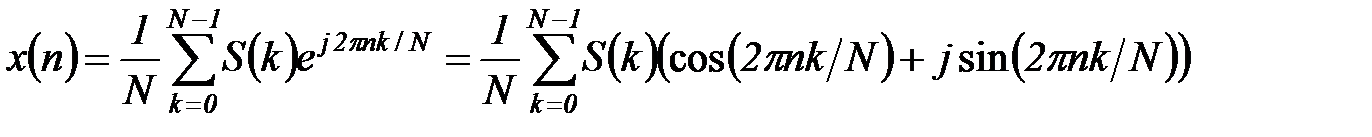. (5.53)