Гладкие динамические системы
В этом случае множество моментов времени совпадает с вещественной осью: 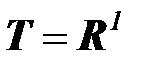 (непрерывное время),
(непрерывное время),
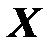 - множество действительных n-векторов,
- множество действительных n-векторов, 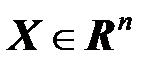 ,
,
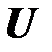 - множество действительных m-векторов,
- множество действительных m-векторов, 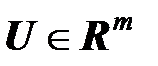 ,
,
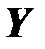 - множество действительных k-векторов,
- множество действительных k-векторов,  ,
,
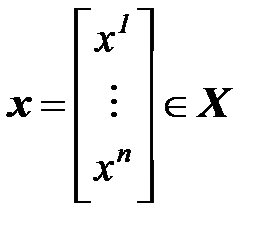 -
- 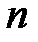 - вектор состояния,
- вектор состояния,
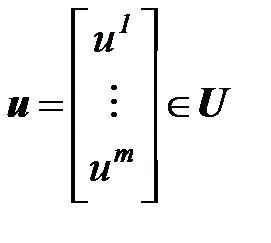 -
- 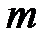 - вектор управления,
- вектор управления,
 -
- 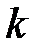 - вектор наблюдений.
- вектор наблюдений.
Все эти векторы являются функциями времени.
Переходная функция  системы å в этом случае является решением дифференциального уравнения
системы å в этом случае является решением дифференциального уравнения
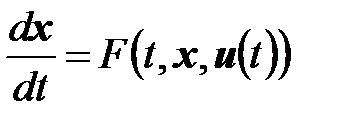 , (6.1)
, (6.1)
а выходное отображение определяется преобразованием
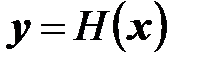 , (6.2)
, (6.2)
где 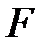 и
и 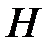 - векторные функции соответствующих размерностей.
- векторные функции соответствующих размерностей.
6.5.2 Системы с дискретным временем
Многие современные системы управления основаны на принципе цифровой обработки информации. Сигналы в таких устройствах представляют собой последовательность импульсов, квантованных по времени, т.е. определенных в равноотстоящие моменты времени
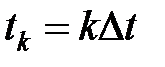 ,
, 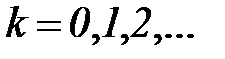 ,
,
где 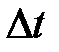 - малый временной шаг. При этом множество
- малый временной шаг. При этом множество
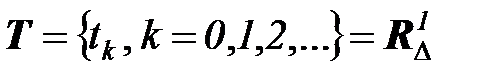
является дискретным (решетчатым).
Множества состояний, управляющих воздействий и наблюдений также являются дискретными: 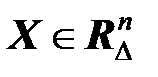 ,
, 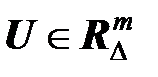 ,
, 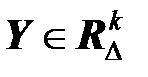 .
.
В этом случае все векторы, определяющие динамическую систему, заданы на временной решетке и зависят от индекса  :
:
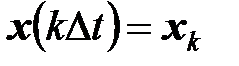 ,
, 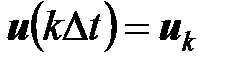 ,
, 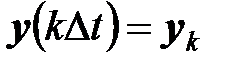 .
.
Для систем с дискретным временем переходная функция является решением разностного уравнения
 , (6.3)
, (6.3)
а выходное отображение аналогично (6.2):
 , (6.4)
, (6.4)
где 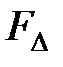 и
и 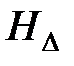 - векторные функции.
- векторные функции.
Отметим, что в данном пособии и впредь мы будем нижним индексом D отмечать объекты, рассматриваемые в дискретном времени.
Представление управляемых динамических систем в дискретном времени весьма удобно и естественно при использовании цифровых управляющих устройств, поскольку в этом случае расчет всех параметров и выдача управляющих воздействий задаются шагами алгоритма управления.
6.5.3 Линейные динамические системы
1. Системы с непрерывным временем.В том случае, когда функции 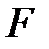 и
и 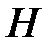 в уравнениях (6.1), (6.2) линейны по своим аргументам, получаем линейную гладкую динамическую систему å с непрерывным временем
в уравнениях (6.1), (6.2) линейны по своим аргументам, получаем линейную гладкую динамическую систему å с непрерывным временем
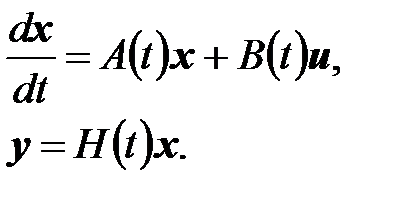 (6.5)
(6.5)
Если матрицы А, В, 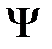 не зависят от времени, то система å называется стационарной. В этом случае ее уравнения имеют вид
не зависят от времени, то система å называется стационарной. В этом случае ее уравнения имеют вид
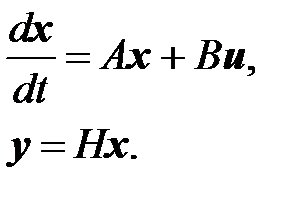 (6.6)
(6.6)
Системы (6.4) и (6.5) дополняются начальными условиями: при 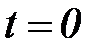
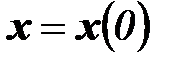 .
.
Первое уравнение системы (6.5) можно формально записать в виде
 .
.
Тогда взаимодействие сигналов в системе может быть представлено так, как показано на рисунок 6.3. Двойные стрелки на рисунке обозначают векторный сигнал.

Рисунок 6.3 Структурная схема линейной динамической системы
Наряду с представлением линейных динамических систем в виде системы из  дифференциальных уравнений первого порядка вида (6.5) или (6.6) в теории систем часто используется эквивалентная форма представления системы в виде одного дифференциального уравнения
дифференциальных уравнений первого порядка вида (6.5) или (6.6) в теории систем часто используется эквивалентная форма представления системы в виде одного дифференциального уравнения  -го порядка.
-го порядка.
2. Системы с дискретным временем.Аналогично (6.6) для стационарных систем модель (6.3) примет вид:
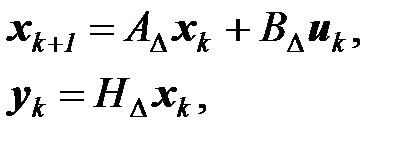 (6.7)
(6.7)
где 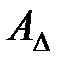 ,
, 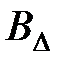 ,
,  - матрицы соответствующих размерностей.
- матрицы соответствующих размерностей.
Взаимодействие сигналов в системе с дискретным временем согласно (6.7) также может быть представлено в виде схемы на рисунке 6.3 с теми отличиями, что блок интегрирования заменяется блоком суммирования, а сигнал обратной связи задерживается на один такт.
Покажем, как можно перейти от модели системы с непрерывным временем к системе с дискретным временем.
Положим, что система содержит квантователь сигнала (Рисунок 6.3) и
при 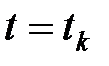
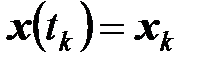 ,
, 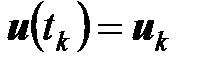 ,
, 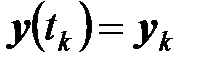 ,
,  мало и производная
мало и производная 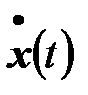 приближенно равна
приближенно равна
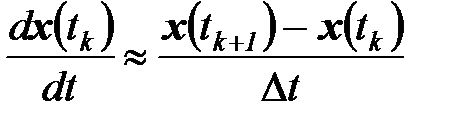 .
.
Тогда формулы (6.5) примут вид:
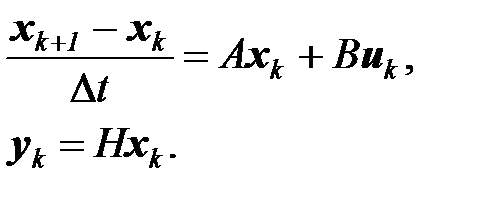
Выполнив преобразования в первой формуле, приведем систему к виду (6.7), где матрицы определяются следующим образом:
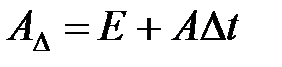 ,
,  ,
,  ,
,
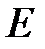 - единичная матрица размерности
- единичная матрица размерности 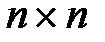 .
.
При 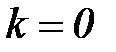 должен быть задан вектор
должен быть задан вектор  .
.
Не вызывает трудностей и обратный переход - от модели динамической системы в дискретном времени (6.7) к модели в непрерывном времени (5.6). В этом случае в уравнении нужно выделить разность 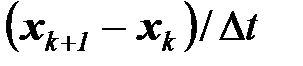 и заменить ее производной
и заменить ее производной 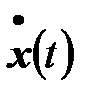 , где
, где 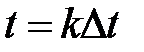 .
.
6.5.4 Переходные функции линейных динамических систем
В данном параграфе мы кратко рассмотрим аналитические решения уравнений динамики линейных систем. При этом будут использованы известные результаты теории дифференциальных уравнений.
1. Переходные функции линейных систем с непрерывным временем.Аналитическое решение уравнения (6.6) при векторе начальных условий 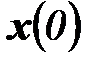 и заданной функции
и заданной функции 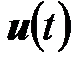 имеет вид
имеет вид
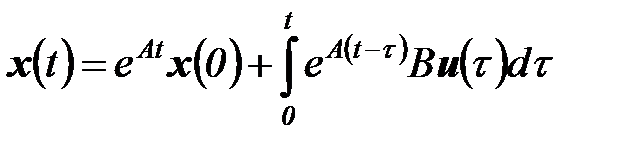 ,
,
или
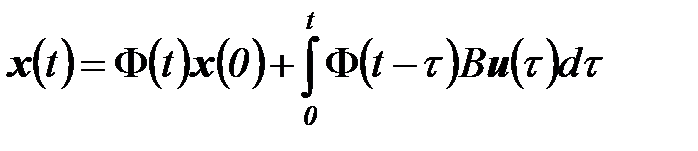 , (6.8)
, (6.8)
где 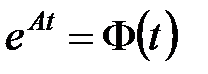 называется фундаментальной матрицей системы (6.8), ее размерность равна n
называется фундаментальной матрицей системы (6.8), ее размерность равна n  n.
n.
Фундаментальная матрица удовлетворяет однородному матричному уравнению

при начальном условии  .
.
Выражение 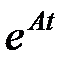 представляет собой матричную экспоненту, которая по аналогии с обычной экспонентой вычисляется в виде ряда
представляет собой матричную экспоненту, которая по аналогии с обычной экспонентой вычисляется в виде ряда
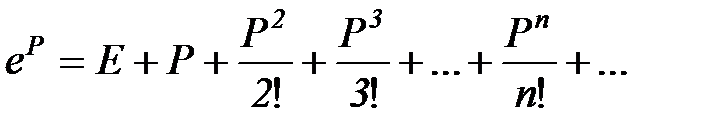 (6.9)
(6.9)
2. Переходные функции линейных динамических систем с дискретным временем.из уравнения (6.6) при заданном 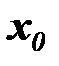 следует цепочка равенств:
следует цепочка равенств:
 ,
,
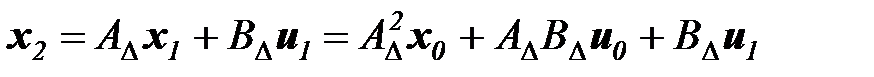 ,
,
и в общем случае:
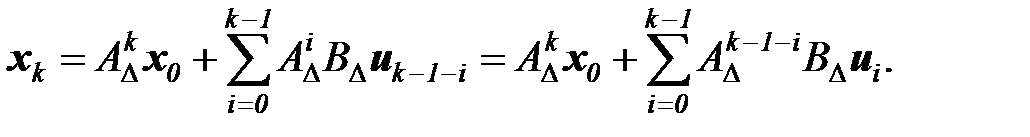 (6.10)
(6.10)
Мы получим формулу, по структуре напоминающую формулу (6.8), в которой операция интегрирования заменена суммированием, а роль фундаментальной матрицы 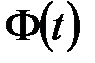 .
.
Представление сложных динамических систем в рассмотренном матричном виде позволяет создать удобные методы их анализа с помощью ЭВМ. Как видно из формул (6.8), (6.9) и (6.10), вычисление переходных функций связано с возведением в высокие степени матриц 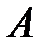 и
и  , задающих параметры динамических систем. Основной математический аппарат, используемый при этом - теория спектрального разложения матриц.
, задающих параметры динамических систем. Основной математический аппарат, используемый при этом - теория спектрального разложения матриц.
Однако в данном курсе мы эту теорию рассматривать не будем, он будет изложена в курсе «Основы теории управления»
6.5.5 Понятие передаточной функции системы
1. матричные передаточные функции. Мы начнем рассмотрение понятия передаточных функций со стандартной модели линейной управляемой динамической системы  -го порядка с нулевыми начальными условиями:
-го порядка с нулевыми начальными условиями:
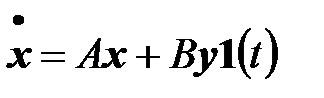 ,
, 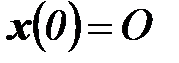 . (6.11)
. (6.11)
Здесь 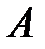 -
-  матрица,
матрица, 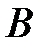 -
-  матрица, O - n -вектор из нулей,
матрица, O - n -вектор из нулей, 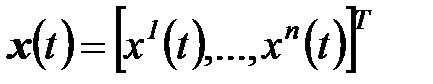 - вектор выходных сигналов,
- вектор выходных сигналов,  - вектор входных сигналов. Умножение сигнала
- вектор входных сигналов. Умножение сигнала 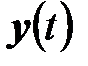 на
на 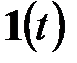 означает, что этот сигнал «включается» при
означает, что этот сигнал «включается» при  .
.
Выбор нулевых начальных условий объясняется тем, что на практике, особенно в случае рассмотрения линеаризованных систем полагают, что при 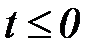 система находится в равновесии в точке
система находится в равновесии в точке  .
.
В координатной форме уравнение (6.11) имеет вид:
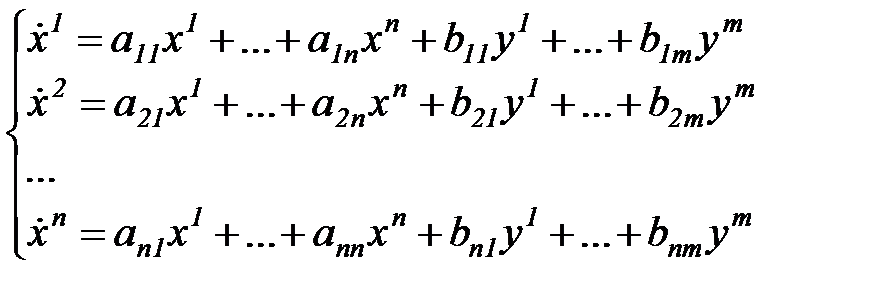 (6.12)
(6.12)
с начальными условиями 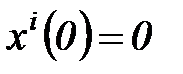 ,
,  .
.
Применив преобразование Лапласа к матричному уравнению (6.11) и воспользовавшись правилом получения изображения производных функций (свойство 7, преобразования Лапласа, п. 5.3.1) при нулевых начальных условиях, получим:
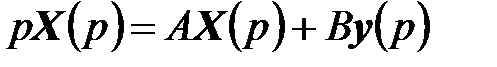 ,
,
откуда 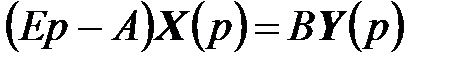 ,
,
где 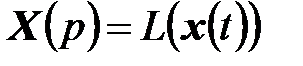 ,
, 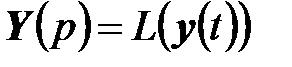 - векторы изображений соответствующих размерностей, E - единичная матрица размерности
- векторы изображений соответствующих размерностей, E - единичная матрица размерности 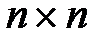 .
.
Из последнего выражения следует
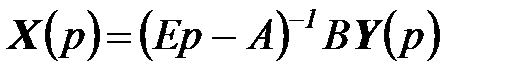
или
 ,
,
где
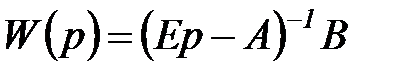 . (6.13)
. (6.13)
Множитель 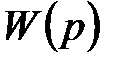 , связывающий изображение вектора выходных сигналов
, связывающий изображение вектора выходных сигналов 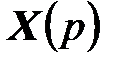 с изображением вектора входных сигналов
с изображением вектора входных сигналов 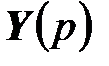 , называют матричной передаточной функцией системы (6.11)
, называют матричной передаточной функцией системы (6.11)
2. Динамическая система, заданная дифференциальным уравнением 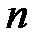 -го порядка. Пусть динамическая система задана дифференциальным уравнением
-го порядка. Пусть динамическая система задана дифференциальным уравнением
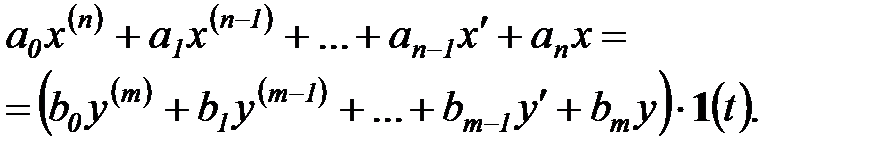 (6.14)
(6.14)
Здесь 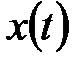 - выходной сигнал,
- выходной сигнал, 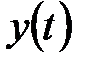 - входной сигнал,
- входной сигнал, 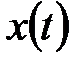 и
и  - скалярные функции. Система (6.14) рассматривается при нулевых начальных условиях:
- скалярные функции. Система (6.14) рассматривается при нулевых начальных условиях:
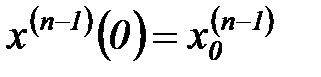 , ...,
, ..., 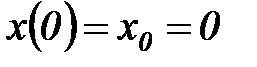 .
.
причем функция 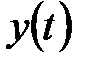 и все ее производные
и все ее производные 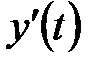 , ...,
, ...,  заданы.
заданы.
Умножение правой части (6.14) на 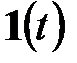 означает, как и выше, что возмущение вместе со своими производными «включается» в момент времени
означает, как и выше, что возмущение вместе со своими производными «включается» в момент времени 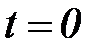 .
.
Применим к обеим частям уравнения (6.14) преобразование Лапласа.
Пусть 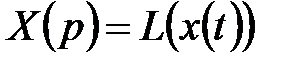 ,
, 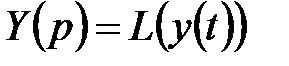 .
.
Используя теорему об изображении суммы, теорему линейности, теорему об изображении производных и нулевые начальные условия функции 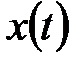 , получим:
, получим:
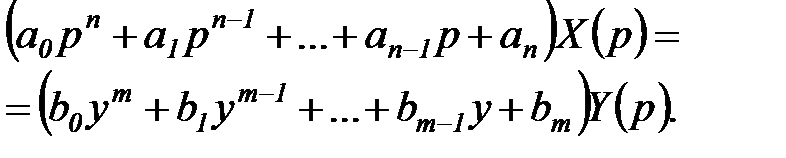 (6.15)
(6.15)
Начальные значения функции 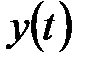 и ее производных не учитываются, т.к. умножение правой части (6.14) на
и ее производных не учитываются, т.к. умножение правой части (6.14) на 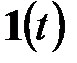 делает их равными нулю при
делает их равными нулю при 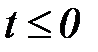 .
.
Отсюда можно получить выражение для изображения выходной величины 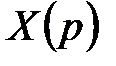 :
:
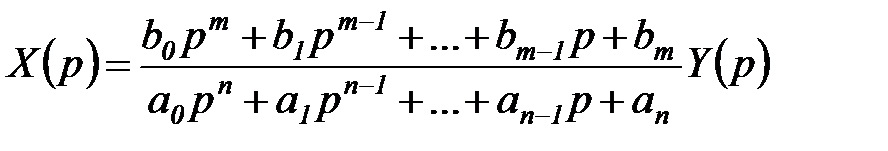 .
.
Обозначим дробь в написанном выражении
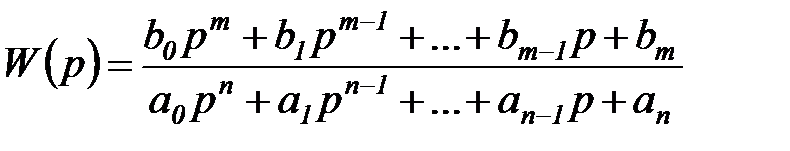 . (6.16)
. (6.16)
Тогда уравнение (26) принимает простой вид
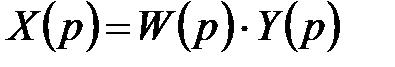 ,
,
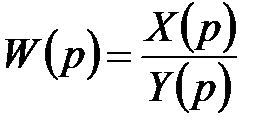 . (6.17)
. (6.17)
Скалярная функция комплексного аргумента 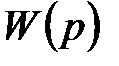 называется передаточной функцией и является одним из основных понятий теории динамических систем, а также многих близких дисциплин - теории управления, теории колебаний, передачи сигналов, теории электрических и радиотехнических устройств и др.
называется передаточной функцией и является одним из основных понятий теории динамических систем, а также многих близких дисциплин - теории управления, теории колебаний, передачи сигналов, теории электрических и радиотехнических устройств и др.
Из формулы (6.17) следует определение:передаточной функцией линейной системы с постоянными коэффициентами называется отношение изображения выходного сигнала системы к изображению входного сигнала системы при нулевых начальных условиях.
При 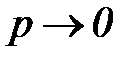 , что, согласно свойствам преобразования Лапласа, соответствует
, что, согласно свойствам преобразования Лапласа, соответствует  , т.е. полному затуханию переходных процессов, имеем
, т.е. полному затуханию переходных процессов, имеем
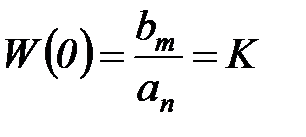 ,
,
где K называется коэффициентом передачи системы и определяет отношение выходного сигнала к входному при установившемся состоянии:
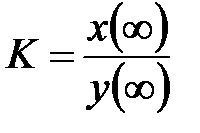 .
.
3. Дискретная передаточная функция. По аналогии с системами непрерывного времени под дискретной передаточной функцией понимают зависящее от 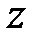 выражение, связывающее
выражение, связывающее  -изображения входного
-изображения входного 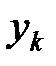 и выходного
и выходного 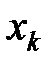 сигналов в динамической системе дискретного времени. Выпишем вид передаточных функций для систем, заданных в векторно-матричной форме и в форме обыкновенного разностного уравнения.
сигналов в динамической системе дискретного времени. Выпишем вид передаточных функций для систем, заданных в векторно-матричной форме и в форме обыкновенного разностного уравнения.
Пусть динамическая система задана системой разностных уравнений первого порядка:
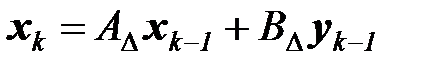 , (6.18)
, (6.18)
где 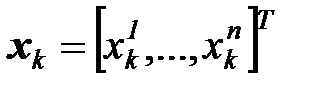 ,
, 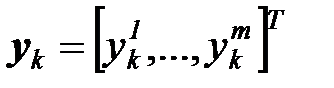 ,
,  -
- 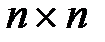 матрица,
матрица, 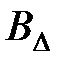 -
-  матрица.
матрица.
Применим 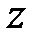 -преобразование к системе (6.18) и с учетом свойств этого преобразования (п.5.4 гл. 5) получим:
-преобразование к системе (6.18) и с учетом свойств этого преобразования (п.5.4 гл. 5) получим:
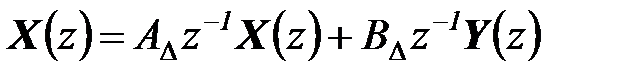 , где
, где 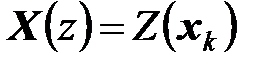 ,
,  .
.
Отсюда 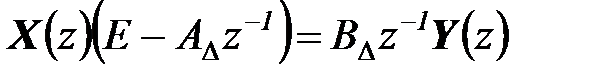 и по аналогии с (6.13) получается матричная дискретная передаточная функция
и по аналогии с (6.13) получается матричная дискретная передаточная функция
 . (6.19)
. (6.19)
Рассмотрим теперь систему, заданную разностным уравнением
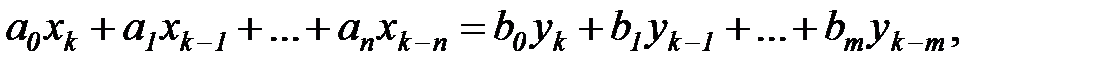
где  и
и 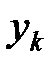 - скалярные переменные.
- скалярные переменные.
Применим к данному уравнению 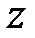 -преобразование и, обозначив
-преобразование и, обозначив 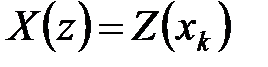 ,
, 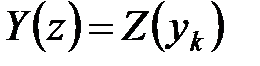 , получим:
, получим:
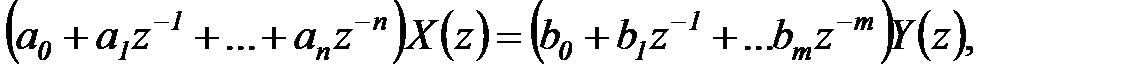
откуда следует выражение для дискретной передаточной функции
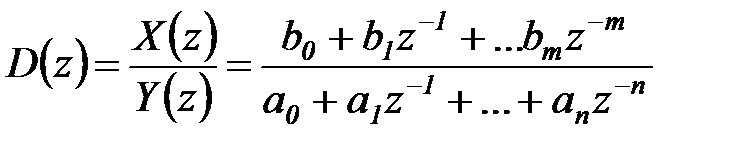 , (6.20)
, (6.20)
которое по структуре напоминает передаточную функцию (6.16).
6.6 Конечные автоматы (F – модели)
Рассмотрим распространенный вид моделей систем, относящийся к F-схемам.
Это – теория автоматов, которую можно рассматривать как частный случай общей теории систем с дискретным временем и дискретным множеством состояний. На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Понятие «автомат» варьируется в зависимости от характера конкретно изучаемых систем, от принятого уровня абстракции и целесообразной степени общности.
Основные соотношения. Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а, следовательно, и множество выходных сигналов) являются конечными множествами.
Абстрактно конечный автомат (по-английски finite automata) можно представить как математическую схему (F-схему),характеризующуюся шестью элементами:
• конечным множеством U входных сигналов (входным алфавитом);
• конечным множеством У выходных сигналов (выходным алфавитом);
• конечным множеством X внутренних состояний (внутренним алфавитом или алфавитом состояний);
• начальным состоянием 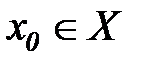 ;
;
• функцией переходов 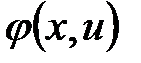 ;
;
• функцией выходов 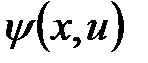 .
.
Автомат, задаваемый F-схемой: 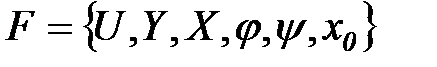 функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие t-мутакту при
функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие t-мутакту при 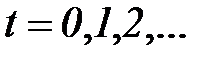 , через
, через 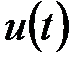 ,
,  ,
,  . При этом, по условию
. При этом, по условию 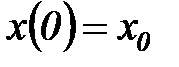 ,
, 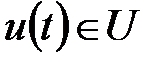 ,
, 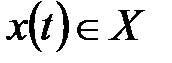 ,
, 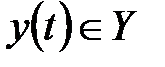 .
.
Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент 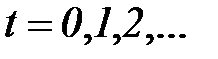 дискретного времени F-автомат находится в определенном состоянии
дискретного времени F-автомат находится в определенном состоянии  из множества X состояний автомата, причем в начальный момент времени
из множества X состояний автомата, причем в начальный момент времени 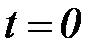 он всегда находится в начальном состоянии
он всегда находится в начальном состоянии 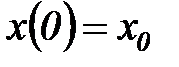 . В момент
. В момент 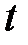 , будучи в состоянии
, будучи в состоянии 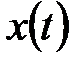 , автомат способен воспринять на входном канале сигнал
, автомат способен воспринять на входном канале сигнал 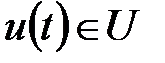 ,
, 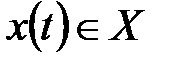 и выдать на выходном канале сигнал
и выдать на выходном канале сигнал 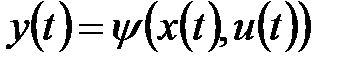 , переходя в состояние
, переходя в состояние 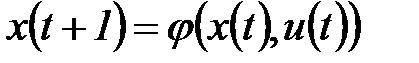 ,
, 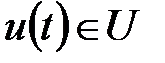 ,
, 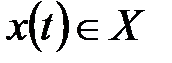 . Говорят, что абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита U на множество слов выходного алфавита У. Другими словами, если на вход конечного автомата, установленного в начальное состояние
. Говорят, что абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита U на множество слов выходного алфавита У. Другими словами, если на вход конечного автомата, установленного в начальное состояние 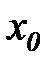 , подавать в некоторой последовательности буквы входного алфавита
, подавать в некоторой последовательности буквы входного алфавита 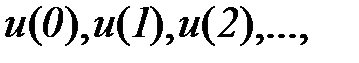 т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита
т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита 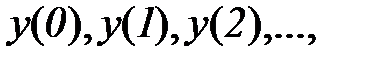 образуя выходное слово.
образуя выходное слово.
Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии 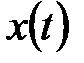 , подается некоторый сигнал
, подается некоторый сигнал 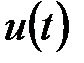 , на который он реагирует переходом в
, на который он реагирует переходом в 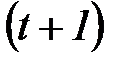 ‑м такте в новое состояние
‑м такте в новое состояние 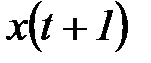 и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили:
и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили:
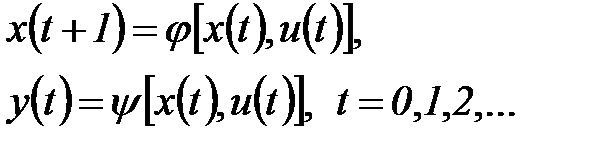 (6.21)
(6.21)
для F-автомата второго рода
 (6.22)
(6.22)
Иными словами, автомат первого рода реагирует на входной сигнал 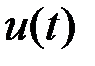 в момент времени
в момент времени  , а автомат второго рода реагирует на входной сигнал
, а автомат второго рода реагирует на входной сигнал 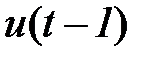 , то есть на сигнал, задержанный на один такт. Наглядно можно определить автомат первого рода как автомат типа «настоящее – настоящее », а автомат второго рода как автомат типа «настоящее – предыдущее».
, то есть на сигнал, задержанный на один такт. Наглядно можно определить автомат первого рода как автомат типа «настоящее – настоящее », а автомат второго рода как автомат типа «настоящее – предыдущее».
Автомат второго рода, для которого
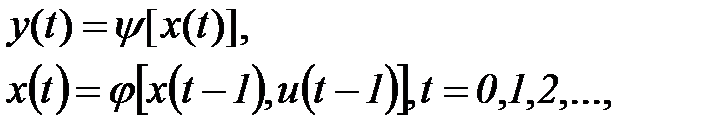 (6.23)
(6.23)
то есть функция выходов не зависит напрямую от входной переменной  , называется автоматом Мура.
, называется автоматом Мура.
Таким образом, уравнения (6.21) – (6.23), полностью задающие F-автомат, являются частным случаем общего описания динамической системы с дискретным временем (6.3), (6.4), когда система детерминированная и на ее единственный вход поступает дискретный сигнал  .
.
По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом, согласно (6.21), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу  определенный выходной сигнал то есть реализует логическую функцию вида (6.23).
определенный выходной сигнал то есть реализует логическую функцию вида (6.23).
 Эта функция называется булевой, если алфавиты U и Y, которым принадлежат значения сигналов x и y, состоят из двух букв.
Эта функция называется булевой, если алфавиты U и Y, которым принадлежат значения сигналов x и y, состоят из двух букв.
По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F - автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» и в соответствии с уравнениями (6.21) – (6.23) происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F – автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины 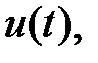 он может, как следует из (6.21) – (6.23), несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.
он может, как следует из (6.21) – (6.23), несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.
Возможные приложения. Для того, чтобы задать конечный F-автомат, необходимо описать все элементы множества 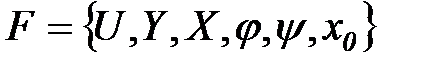 , то есть входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние
, то есть входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние 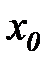 , в котором автомат находился в момент времени
, в котором автомат находился в момент времени 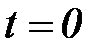 . Существует несколько способов задания работы F – автоматов, но наиболее часто используются табличный, графический и матричный.
. Существует несколько способов задания работы F – автоматов, но наиболее часто используются табличный, графический и матричный.
Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы – его состояниям. При этом обычно первый слева столбец соответствует начальному состоянию 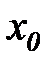 . На пересечении i- й строки и j -го столбца таблицы переходов помещается соответствующее значение
. На пересечении i- й строки и j -го столбца таблицы переходов помещается соответствующее значение 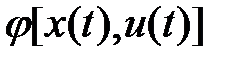 функции переходов, а в таблице выходов – соответствующее значение
функции переходов, а в таблице выходов – соответствующее значение  функции выходов.
функции выходов.
В заключение отметим, что концепция конечных автоматов получила применение в программировании. Профессором А.А. Шалыто в 1991 г. был предложен новый стиль программирования, названный им «автоматное программирование», основанный на применении конечных автоматов для описания поведения программ (http://is.ifmo.ru/). В автоматном программировании конечные автоматы используются для описания поведения программ при их спецификации, проектировании, реализации, отладке, документировании и сопровождении. Под термином «автоматное программирование» понимается не только построение и реализация конечных автоматов, но и проектирование и реализация программ в целом, поведение которых описывается автоматами. Существуют различные модели для описания конечных автоматов. Однако их представление в виде графов переходов (диаграмм состояний) наиболее удобно для человека.
6.7 Модели дискретно – статистического типа (P - модели)
В настоящем параграфе мы рассмотрим вероятностные модели информационных процессов. Наиболее простой класс вероятностных моделей дискретно-стохастического типа (P – схемы по рассмотренной ранее классификации) образуют цепи Маркова, названные так по имени известного русского математика А.А. Маркова, разработавшего эту теорию в 1907 году. Большой вклад в теорию цепей Маркова внес академик А.Н. Колмогоров. Возможности теории цепей Маркова далеко выходят за рамки описания информационных процессов и систем. Эта теория широко применяется в физике, биологии, социологии, экономике, технике и целом ряде других наук.
Математический аппарат цепей Маркова позволяет оценивать многие характеристики информационных процессов систем, такие как вероятное время завершения определенных этапов работы, средняя производительность, среднее время безотказной работы и другие. Здесь приводятся только начальные сведения об этих моделях. Более подробно теория и применение цепей Маркова рассматривается в специальной литературе [13] и курсе «Моделирование систем» [17] .
6.6.1 Определение цепи Маркова
Рассмотрим систему å, находящуюся в каждый из дискретных моментов 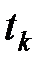 в одном из
в одном из  состояний
состояний 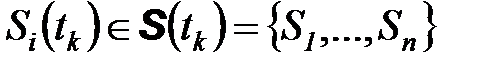 .
.
Система рассматривается в множество моментов времени  . В каждый момент времени система может находиться только в одном из состояний. Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей
. В каждый момент времени система может находиться только в одном из состояний. Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей
 . (6.24)
. (6.24)
Каждый элемент матрицы 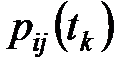 показывает вероятность того, что если å в момент
показывает вероятность того, что если å в момент 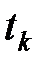 находилось в состоянии
находилось в состоянии  , то в момент
, то в момент 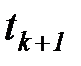 она окажется в состоянии
она окажется в состоянии 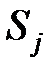 :
:
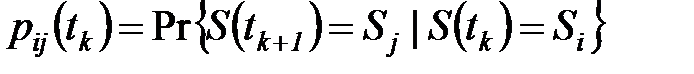 (6.25)
(6.25)
Причем (и это основное свойство марковских процессов) вероятность перехода из 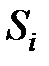 в
в 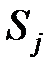 не зависит от предыдущих состояний.
не зависит от предыдущих состояний.
Понятно, что переходы во все возможные состояния (в том числе в себя) образуют полную группу событий, поэтому 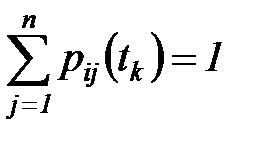 для всех
для всех 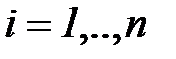 ,
,  .
.
Пусть вектор-строка  - описывает распределение вероятностей нахождения å в соответствующих состояниях в момент
- описывает распределение вероятностей нахождения å в соответствующих состояниях в момент  , то есть
, то есть 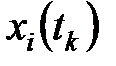 - это вероятность того, что в момент
- это вероятность того, что в момент 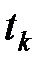 å находится в состоянии
å находится в состоянии  . При этом
. При этом 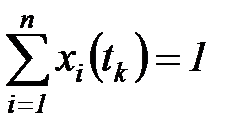 ,
,  Тогда по теореме об умножении вероятностей и с учетом основного свойства марковского процесса получим:
Тогда по теореме об умножении вероятностей и с учетом основного свойства марковского процесса получим:
 (6.26)
(6.26)
где 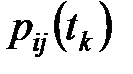 выступают в роли условных вероятностей перехода в состояние
выступают в роли условных вероятностей перехода в состояние 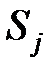 при условии, что система находится в состоянии
при условии, что система находится в состоянии  .
.
Нетрудно видеть, что правая часть написанной формулы определяет произведение вектора 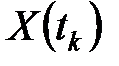 на матрицу
на матрицу  и в векторной форме эквивалентна следующей записи динамического процесса:
и в векторной форме эквивалентна следующей записи динамического процесса:
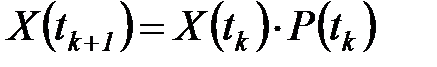 . (6.27)
. (6.27)
Последовательность состояний 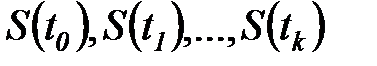 называется конечной цепью Маркова. Цепь называется однородной, если
называется конечной цепью Маркова. Цепь называется однородной, если  не зависит от времени.
не зависит от времени.
В этом случае рекуррентная формула (6.27) может быть записана в виде
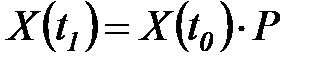 ,
,
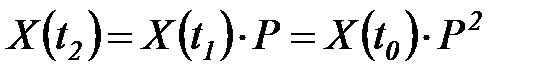 ,
,
…·
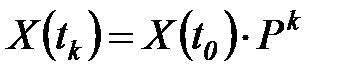 , (6.28)
, (6.28)
где 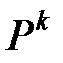 - k-я степень матрицы P.
- k-я степень матрицы P.
Нетрудно убедиться, что сумма вероятностей нахождения системы во всех состояниях (т.е. сумма элементов вектора 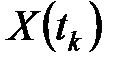 ) на каждом шаге остается равной единице.
) на каждом шаге остается равной единице.
Последовательность векторов  определяет динамику моделируемого процесса.
определяет динамику моделируемого процесса.
Цепь Маркова можно представить как динамическую систему (рисунок 6.4), в которой прямоугольник 1 представляет собой задержку на 1 такт.

Рисунок 6.4 Цепь Маркова как динамическая система
Отметим, что матрицы P, порождающие цепи Маркова, т.е. такие, у которых все элементы 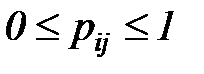 , а их суммы по столбцам равны единице для всех строк:
, а их суммы по столбцам равны единице для всех строк:
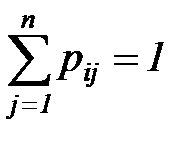 ,
, 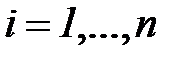
называют стохастическими.
Множество состояний 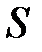 в рассматриваемой модели подразделяется на множество невозвратных состояний
в рассматриваемой модели подразделяется на множество невозвратных состояний 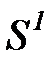 и множество поглощающих состояний
и множество поглощающих состояний 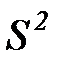 . Состояния, относящиеся к множеству
. Состояния, относящиеся к множеству 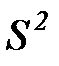 , соответствуют завершению процесса. Поэтому, исключив из матрицы
, соответствуют завершению процесса. Поэтому, исключив из матрицы  строки и столбцы, соответствующие состояниям из
строки и столбцы, соответствующие состояниям из 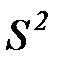 и обозначив оставшуюся матрицу
и обозначив оставшуюся матрицу 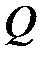 , можем вычислить так называемую фундаментальную матрицу цепи Маркова:
, можем вычислить так называемую фундаментальную матрицу цепи Маркова:
 , (6.29)
, (6.29)
где I – единичная матрица.
Каждый элемент 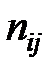 матрицы
матрицы 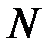 представляет собой среднее число пребываний процесса в состоянии Sj при старте из состояния
представляет собой среднее число пребываний процесса в состоянии Sj при старте из состояния  .В том случае, когда старт происходит из состояния
.В том случае, когда старт происходит из состояния  , достаточно рассматривать только первую строку матрицы
, достаточно рассматривать только первую строку матрицы 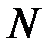 .
.
Зная 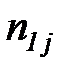 , можно вычислить среднюю трудоемкость процесса по формуле
, можно вычислить среднюю трудоемкость процесса по формуле
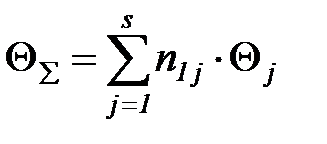 , (6.30)
, (6.30)
где -  трудоемкость j – го шага процесса в соответствующих единицах.
трудоемкость j – го шага процесса в соответствующих единицах.
В ряде случаев исследователя может интересовать оценка дисперсии трудоемкости процесса. Для этой цели вычисляется матрица дисперсий числа пребываний процесса в множестве невозвратных состояний по формуле:
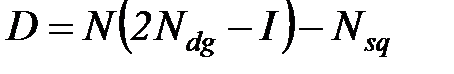 , (6.31)
, (6.31)
где индексы 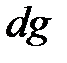 и
и 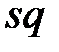 обозначают соответственно выделение диагональных элементов матрицы
обозначают соответственно выделение диагональных элементов матрицы 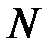 и возведение в квадрат каждого элемента этой матрицы.
и возведение в квадрат каждого элемента этой матрицы.
Ниже мы рассмотрены два примера описания информационных процессов в рамках формализма цепей Маркова.
6.6.2 Модель динамики информационных ресурсов
Рассмотрим методику оценки динамики информационного ресурса, основанную на модели жизненного цикла информационного ресурса, приведенной в первой главе (п.1.2.5)
Пусть имеется множество информационных ресурсов R = { 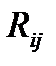 }, где по приведенной выше классификации
}, где по приведенной выше классификации  вид ИР,
вид ИР,  степень актуальности ресурса. Каждый ресурс поступает в информационную систему и проходит в ней весь жизненный цикл.
степень актуальности ресурса. Каждый ресурс поступает в информационную систему и проходит в ней весь жизненный цикл.
Представим жизненный цикл ИР в виде цепи Маркова с дискретным временем, содержащей пять состояний:
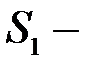 создание ИР,
создание ИР,
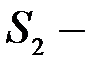 хранение и обработка ИР критической важности,
хранение и обработка ИР критической важности,
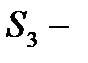 хранение и обработка ИР с важной информацией,
хранение и обработка ИР с важной информацией,
 архивирование и хранение ИР с маловажной информацией,
архивирование и хранение ИР с маловажной информацией,
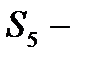 удаление ИР.
удаление ИР.
Граф этой цепи приведен на рисунке 6.5
| 1 |
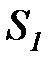
|
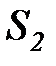
|
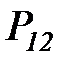
|
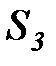
|
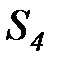
|

|
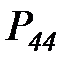
|
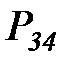
|
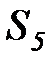
|
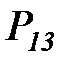
|
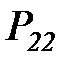
|
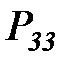
|
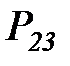
|
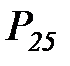
|
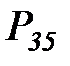
|
Рисунок 6.5. Вероятностная модель жизненного цикла информационного ресурса
Вероятности перехода между состояниями ресурса 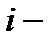 го вида задаются матрицей
го вида задаются матрицей
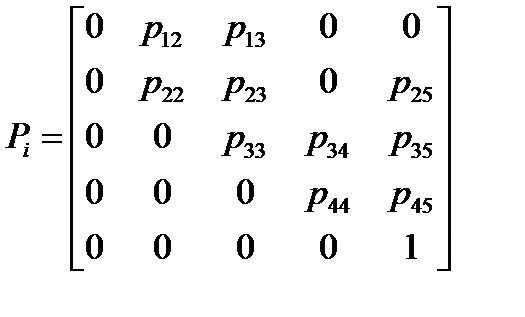 . (6.32)
. (6.32)
Ресурс  характеризуется следующими параметрами:
характеризуется следующими параметрами:
· время поступления ИР в информационную систему 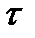 (например, дни, месяцы),
(например, дни, месяцы), 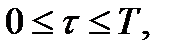 где
где 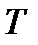 - время исследования системы;
- время исследования системы;
· продолжительность «жизни» ИР 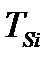 – количество моментов времени от поступления ресурса в систему до момента его удаления с вероятностью, близкой к единице;
– количество моментов времени от поступления ресурса в систему до момента его удаления с вероятностью, близкой к единице;
· объем поступившего ресурса  - го вида в момент
- го вида в момент 
 , Мбайт;
, Мбайт;
·  объем ресурса
объем ресурса  , Мбайт, в момент
, Мбайт, в момент 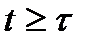 . Величины
. Величины 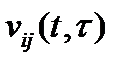 образуют вектор
образуют вектор 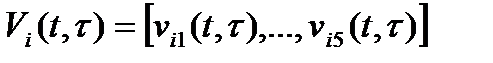 , при этом
, при этом 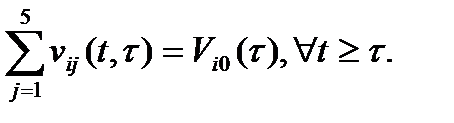
· 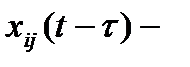 вероятность нахождения ресурса
вероятность нахождения ресурса  в
в 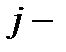 степени актуальности в момент
степени актуальности в момент 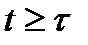 . Вероятности
. Вероятности 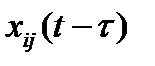 образуют вектор
образуют вектор  , при этом
, при этом 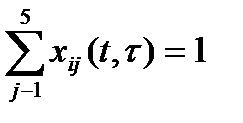 , начальное распределение вероятностей
, начальное распределение вероятностей 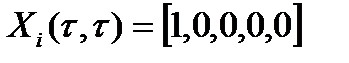 .
.
Ресурс, поступивший в систему (в состояние  ), в дальнейшем перераспределяется между состояниями пропорционально вероятностям пребывания системы в данном состоянии. Исходя из сказанного, мы получим следующие расчетные формулы.
), в дальнейшем перераспределяется между состояниями пропорционально вероятностям пребывания системы в данном состоянии. Исходя из сказанного, мы получим следующие расчетные формулы.
Динамика изменения состояния ИР определится уравнениями:
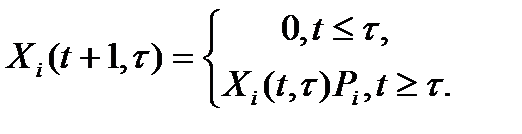 (6.33)
(6.33)
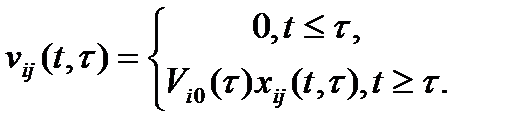 (6.34)
(6.34)
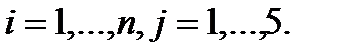
Общий объем ресурсов 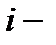 го вида, находящихся в системе, определится вектором
го вида, находящихся в системе, определится вектором
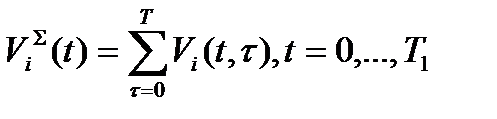 , (6.35)
, (6.35)
где  время жизни ресурса
время жизни ресурса 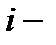 го вида.
го вида.
Общий объем ресурсов 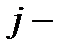 ой степени актуальности определится суммой
ой степени актуальности определится суммой
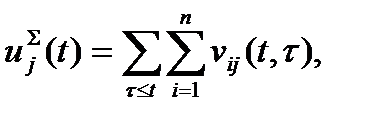 (6.36)
(6.36)
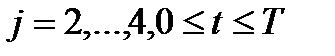
Расчетный объем ИР 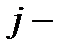 ой степени актуальности
ой степени актуальности 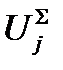 для определения необходимых параметров запоминающего устройства равен максимальному значению величины
для определения необходимых параметров запоминающего устройства равен максимальному значению величины 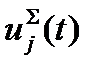 на всем исследуемом интервале времени:
на всем исследуемом интервале времени:
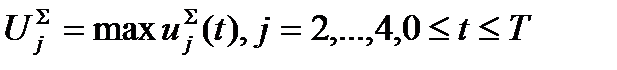 . (6.37)
. (6.37)
Расчеты по формулам (6.33) – (6.36) для матрицы (6.22) и исходных данных по объемам поступающих ресурсов удобно производить с помощью специальной программы [32].
Пример.Рассмотрим систему, содержащую информационный ресурс, динамика которого задается матрицей 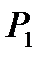
 ,
,
Предположим, что на вход системы в каждый момент времени поступает ресурс в объеме 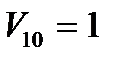 Мбайт. Расчет, проведенный по формулам (6.33) – (6.35) позволяет оценить динамику накопления ИР в системе. Результаты расчета приведены на рисунке 6.6.
Мбайт. Расчет, проведенный по формулам (6.33) – (6.35) позволяет оценить динамику накопления ИР в системе. Результаты расчета приведены на рисунке 6.6.
а
б
Рисунок 6.6. Графики жизненного цикла информационного ресурса за 100 шагов, динамика которого задана матрицей 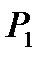 : а) – вероятности нахождения единичного ИР в разных степенях актуальности; б) – динамика накопления ИР.
: а) – вероятности нахождения единичного ИР в разных степенях актуальности; б) – динамика накопления ИР.
Дата добавления: 2016-06-13; просмотров: 1873;
