Пример построения линейной модели процесса.

При исследовании процесса, который характеризуется тремя входными 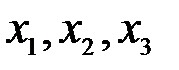и одним выходным параметром 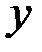, было проведено 15 наблюдений, которые сведены в таблицу 7.4. Для того, чтобы оценить величину свободного члена в уравнении регрессии, вводим фиктивную переменную 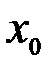, которая равна единице для всех экспериментов.

Основные статистические характеристики переменных приведены в таблице 7.5.

Корреляционная матрица переменных содержится в таблице 7.6.

Линейная модель, описывающая взаимосвязь между входными и выходной переменными, полученная по методу наименьших квадратов, имеет вид:

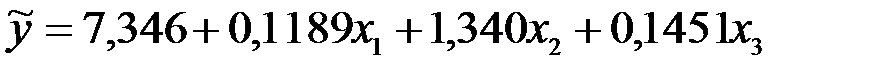При этом остаточная дисперсия равна:

,

критерий Фишера:

.

Таблица 7.4

Экспериментальные данные для построения модели процесса

j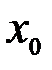
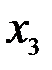
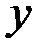
		61,7	3,5	6,7	17,6
		63,5	3,0	5,5	18,4
		59,5	2,1	6,3	16,7
		63,0	2,7	5,0	18,1
		58,0	1,7	4,2	16,2
		61,5	2,5	5,2	17,4
		60,0	2,0	4,0	16,8
		64,5	1,1	5,0	15,3
		59,7	2,0	3,3	16,5
		55,2	1,5	4,0	15,3
		53,7	0,8	2,7	14,4
		52,6	0,5	3,2	13,8
		55,6	1,2	2,3	15,1
		55,0	0,3	2,8	14,0
		52,5	0,7	1,5	14,1

Основные статистические характеристики переменных приведены в таблице 7.5.

Таблица 7.5

Основные статистические характеристики процесса

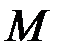
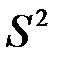
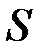
	58,4	16,48	4,06
	1,7	0,91	0,95
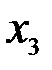
	4,11	2,25	1,5
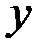
	15,98	2,35	1,53

Таблица 7.6

Корреляционная матрица переменных процесса

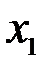
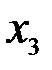
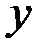
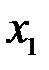
		0,76	0,78	0,84
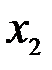
	0,76		0,79	0,96
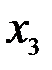
	0,78	0,79		0,77
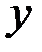
	0,84	0,96	0,77

Из сравнения оценок и с 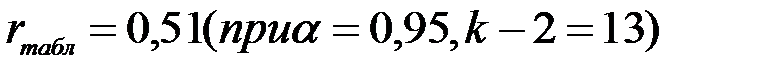(см. табл. 7.3) видно, что все они статистически значимы, т.к. r>r_табл .

Входные переменные по степени их влияния на выходную величину можно расположить в такой последовательности: .

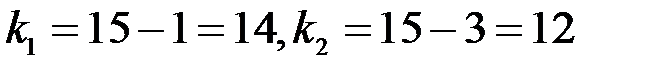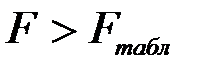Оценим теперь адекватность модели в целом. По таблице для значений критерия Фишера [29] при находим . В нашем случае , следовательно, полученная модель адекватно отражает экспериментальные данные.

7.3 Оценка параметров цепи Маркова по экспериментальным данным

При моделировании процессов на основе цепей Маркова возникает вопрос – как оценивать параметры модели. Идентификация параметров моделей, описанной в параграфе 6.5, заключается в оценке вероятностей перехода между состояниями процесса, а также в оценке трудоемкостей всех его этапов. Эти параметры могут оцениваться различными методами: экспертно на основе опыта, на основе нормативных документов, а также путем обработки наблюдений за реальным процессом. Последний случай идентификации рассмотрен ниже.

7.3.1 Оценка вероятностей перехода между состояниями процесса

В данном разделе описана методика оценки вероятностей перехода между состояниями процесса путем обработки наблюдений за этим процессом [21].

Методика заключается в следующем. При изучении процесса функционирования системы составляется протокол прохождения каждым транзактом всех этапов процесса. Такой протокол рассматривается как одна реализация случайного процесса, порожденного цепью Маркова (см. п. 6.5). Строка в матрице соответствует состоянию, из которого начат очередной шаг процесса, а столбец – состоянию, в котором оказывается процесс на следующем шаге. В каждую ячейку матрицы, где оказался процесс, заносится единица.

Процесс перехода от шага к шагу фиксируется учетным модулем системы управления, что после накопления необходимого объема статистических данных позволяет произвести оценку параметров модели – вероятностей перехода между состояниями.

Проведя суммирование данных протоколов всех транзактов по строкам, и разделив накопленные в каждой ячейке числа на сумму строки, можно получить оценки вероятностей перехода из одного состояния в другие, т.е. матрицу P.

Рассмотрим получение таких оценок более подробно.

Введем величину 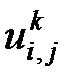– индикатор событий, т.е. количество попаданий в состояние 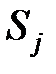при старте из состояния 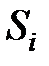в 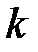- м протокол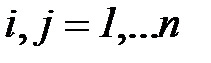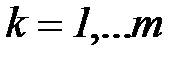е, ; , где 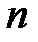- количество состояний модели (количество шагов бизнес-процесса), - количество обрабатываемых протоколов.

на основе определения цепи Маркова вероятность перехода в состояние при старте из состояния 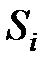может быть оценена следующим образом.

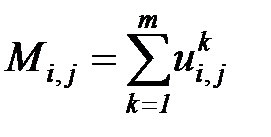; – число попаданий процесса в состояние 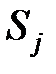при старте из 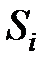по всем протоколам;

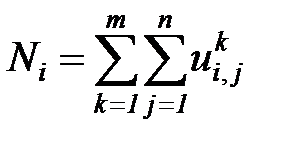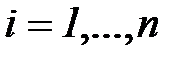; – число попаданий во все состояния 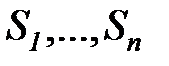при старте из 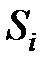по всем протоколам.

Тогда оценка вероятности перехода из 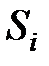в 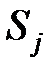, вычисленная по методу наибольшего правдоподобия [21], определится формулой

; (7.26)

Доверительная оценка полученных вероятностей может быть вычислена в нашем случае на основе уравнения

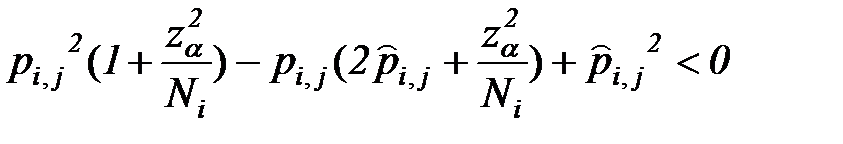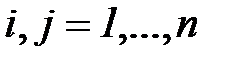, . (7.27)

Здесь 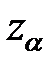- величина, зависящая от уровня надежности оценки. В част-ности, при 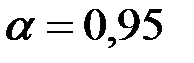величина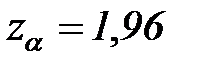

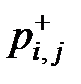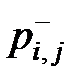Корни этого уравнения и представляют собой верхнюю и нижнюю границу возможных значений оценки вероятности 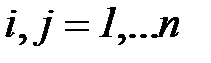. Из уравнения (7.27) видно, что с увеличением числа наблюдений 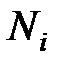верхняя и нижняя оценки сближаются и стремятся к средней оценке вероятности 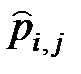. В то же время, при уменьшении числа наблюдений верхняя и нижняя оценки значительно расходятся, что приводит к неопределенности величины .

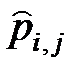Корни неравенства (7.27) 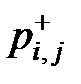и 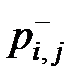будут иметь вид:

.

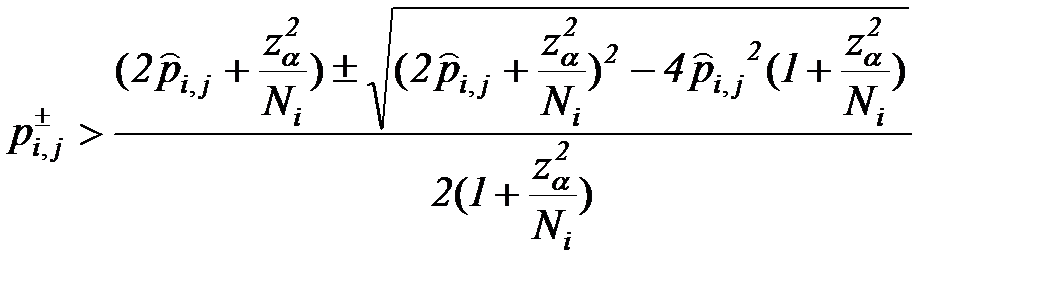Отсюда

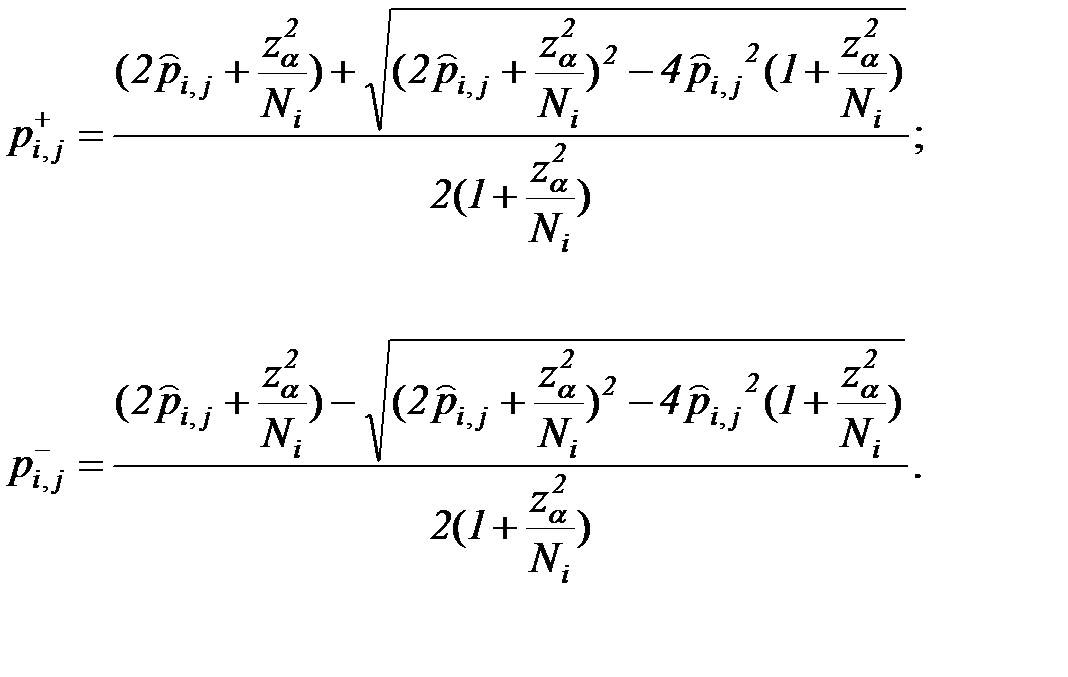(7.28)

7.3.2. Оценка чувствительности модели к изменению вероятностей перехода между состояниями

Как видно из предыдущего раздела, оценки вероятностей перехода между состояниями имеют разброс, зависящий от числа обработанных транзактов и количества зафиксированных переходов между состояниями бизнес-процесса. Поэтому важно оценить, как этот разброс скажется на конечных результатах моделирования динамики процесса.

Итак, предположим, что матрица вероятностей переходов между состояниями имеет вид

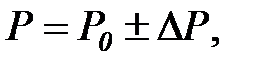(7.29)

где 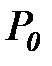- среднее значение оценки матрицы, 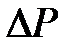- разброс относительно среднего.

Тогда оценка вероятностей нахождения в различных состояниях определится согласно (7.27) формулой

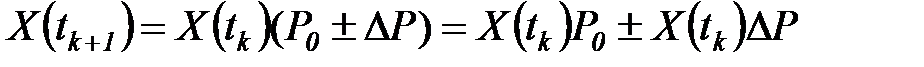, (7.30)

в которой второе слагаемое определяет возможный разброс вероятностей пребывания в различных состояниях на 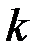-м шаге процесса.

Рассмотрим теперь, как влияет разброс значений матрицы 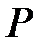на величину матрицы 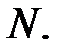Выделим в матрице 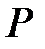подматрицу 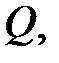отвечающую за обмен между невозвратными состояниями и представим ее в виде

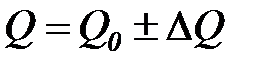, (7.31)

где 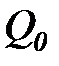- среднее значение оценки матрицы, - матрица, определяющая разброс вероятностей относительно среднего значения. Будем считать, что норма матрицы 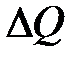мала. Вследствие изменения матрицы 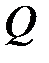изменится также матрица 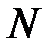и примет значение 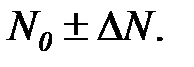Оценим приращение 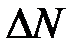этой матрицы. В силу (6.29 гл. 6) имеем:

,

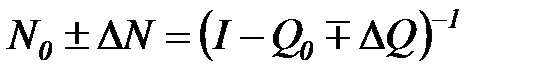откуда

.

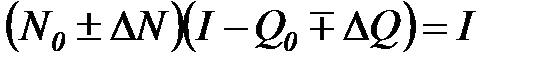Перемножив выражения в скобках, получим:

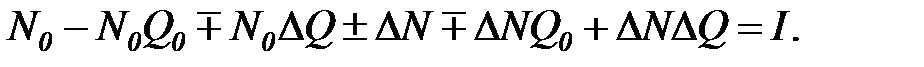(7.32)

Отбросим произведение 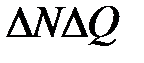как матрицу, норма которой имеет второй порядок малости, и сгруппируем оставшиеся члены:

,

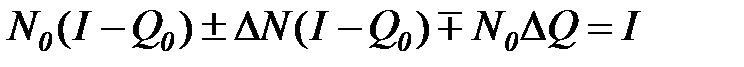откуда следует

,

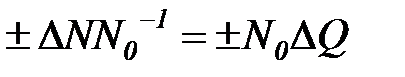и окончательно

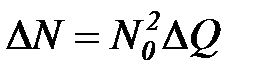. (7.33)

На основе выражения (7.33) можно оценивать разброс числа пребываний процесса во множестве невозвратных состояний, если известен разброс вероятностей перехода между состояниями внутри этого множества.

Пример

При исследовании системы, содержащей 6 состояний, были получены следующие значения числа пребываний в различных состояниях, которые сведены в матрицу :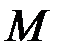

.

Требуется по этим данным построить модель системы в виде цепи Маркова и оценить ее характеристики.

1. Подсчитаем сумму элементов каждой строки – общее число попаданий в каждое из состояний:

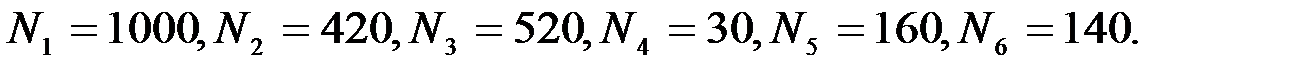
Обработка матрицы 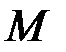по формуле (7.26) позволяет получить матрицу оценок вероятностей переходов между состояниями:

.

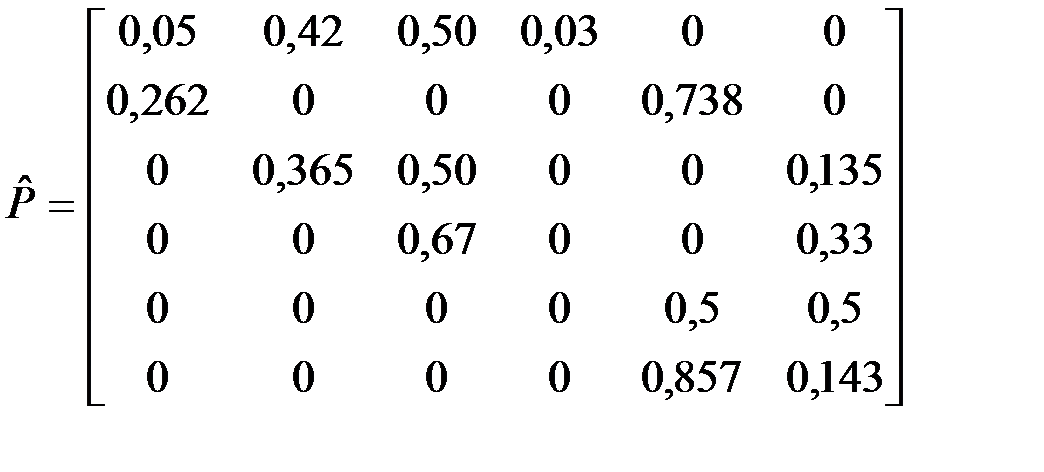2. Вычислим разброс вероятностей по формулам (7.28) и получим матрицы 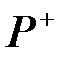и :

,

.

Обратим внимание на то, что матрицы 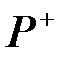и 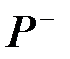не являются стохастическими, так как в них сумма элементов по строкам не равна единице.

3. Вычислим оценку среднего числа пребываний процесса в множестве невозвратных состояний по формуле (7.49):

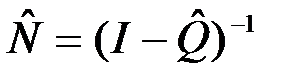
и дисперсию этих величин по формуле (6.31 гл. 6):

.

В нашем случае, как видно из структуры матриц 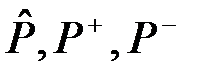, невозвратное множество образуют первые четыре состояния, и матрицы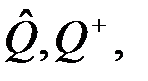 имеют вид:

,

,

,

,

4. Вычислим отклонение верхней оценки вероятностей от ее среднего значения:

.

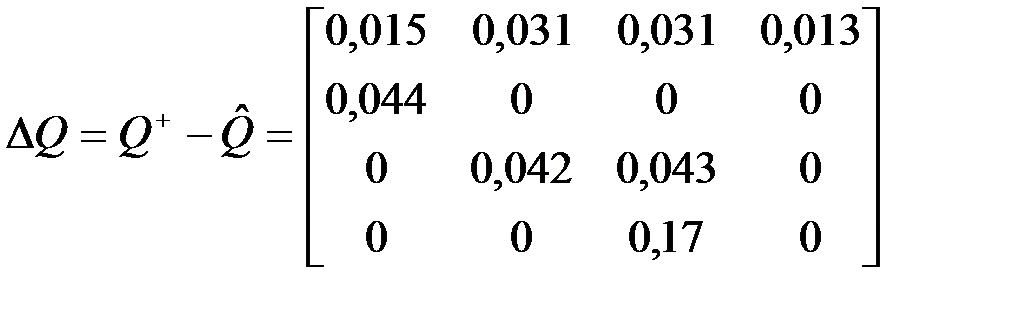В соответствии с формулой (7.33) разброс числа пребывания процесса в множестве невозвратных состояний, вызванный разбросом вероятностей определится матрицей:

.

Мы видим, что наиболее нагруженным узлом данной системы является третий. Это видно по исходным данным – третьему столбцу матрицы , а также третьему столбцу матрицы . Естественно, что и разброс числа пребываний в этом состоянии, определяемый третьими столбцами матриц и , также наибольший среди всех невозвратных состояний. Наименее нагруженным является четвертый узел, что также видно из указанных матриц.