Анимация поведения и интерактивный анализ модели
Удобные средства разработки анимационного представления модели в AnyLogic позволяют представить функционирование моделируемой системы в живой форме динамической анимации, что позволяет "увидеть" поведение сложной системы. Средства анимации позволяют пользователю легко создать виртуальный мир (совокупность графических образов, ожившую мнемосхему и т. п.), управляемый динамическими параметрами модели по законам, определенным пользователем с помощью уравнений и логики моделируемых объектов. Визуальное представление поведения системы помогает пользователю проникнуть в суть процессов, происходящих в системе.
Многие системы моделирования позволяют менять параметры модели только до запуска модели на выполнение. AnyLogic позволяет пользователю вмешиваться в работу модели, изменяя параметры модели в процессе ее функционирования. Поэтому окно анимации можно назвать "стендом" для проведения компьютерного эксперимента с моделью.
Итак, мы видим, что система моделирования AnyLogic обеспечивает поддержку всех этапов имитационного моделирования для различных типов динамических моделей — дискретных, непрерывных и гибридных, детерминированных и стохастических в любых их комбинациях в рамках одного инструмента. Создание модели, ее выполнение, оптимизация параметров, анализ полученных результатов, верификация модели — все эти этапы удобно выполнять в среде AnyLogic. Данный инструмент обладает большим спектром разнообразных возможностей проведения как отдельных прямых экспериментов типа "если-то", так и серий подобных экспериментов для решения всевозможных обратных задач, направленных на поиск параметров модели, оптимизирующих ее функционирование. Удобный интерфейс и различные средства поддержки разработки в AnyLogic делают не только использование, но и создание компьютерных имитационных моделей в этой среде моделирования доступными даже для тех, кто в области вычислительной техники и программирования не является профессионалом.
Глава 7 Методы оценки параметров систем
Методы моделирования, рассмотренные в предыдущей главе, позволяют проводить машинный эксперимент с моделью исследуемой или проектируемой системы. Основная цель экспериментальных исследований состоит в изучении поведения моделируемой системы. Для этого необходимо планировать и проектировать не только саму модель, но и процесс ее использования, т. е. проведение с ней экспериментов на ЭВМ. В зависимости от вида моделей планирование и обработка экспериментов осуществляется разными методами. В данной главе мы рассмотрим общие вопросы планирования эксперимента, а также методы линейной регрессии и методы оценки параметров моделей в виде цепей Маркова.
7.1 О планировании машинного эксперимента
Машинный эксперимент с моделью системы проводится с целью получения информации о характеристиках процесса функционирования рассматриваемого объекта [7]. Эта информация может быть получена как для анализа характеристик, так и для их оптимизации при заданных ограничениях, т. е. для синтеза структуры, алгоритмов и параметров системы. В зависимости от поставленных целей моделирования системы на ЭВМ имеются различные подходы к организации имитационного эксперимента с машинной моделью. Основная задача планирования машинных экспериментов – получение необходимой информации об исследуемой системе при ограничениях на ресурсы (затраты машинного времени, памяти и т. п.).
Машинный эксперимент.Эффективность машинных экспериментов с моделями существенно зависит от выбора плана эксперимента, так как именно план определяет объем и порядок проведения вычислений на ЭВМ, приемы накопления истатистической обработки результатов моделирования системы.Поэтому основная задача планирования машинных экспериментов с моделью формулируется следующим образом: необходимо получить информацию об объекте моделирования, заданном в виде моделирующего алгоритма (программы), при минимальных или ограниченных затратах машинных ресурсов на реализацию процесса моделирования.
Таким образом, при машинном моделировании рационально планировать и проектировать не только саму модель системы, но и процесс ее использования, т. е. проведение с ней экспериментов с использованием компьютеров.
Для планирования эксперимента наиболее важное значение имеют следующие факторы:
1. простота повторения условий эксперимента на ЭВМ с моделью системы;
2. возможность управления экспериментом с моделью, включая его прерывание и возобновление;
3. легкость варьирования условий проведения эксперимента (воздействий внешней среды).
Преимуществом машинных экспериментов перед натурным является возможность полного воспроизведения условий эксперимента с моделью исследуемой системы. Сравнивать две альтернативы возможно при одинаковых условиях, что достигается, например, выбором одной и той же последовательности случайных чисел для каждой из альтернатив. Существенным достоинством перед натурными экспериментами является простота прерывания и возобновления машинных экспериментов, что позволяет применять последовательные и эвристические приемы планирования, которые могут оказаться нереализуемыми в экспериментах с реальными объектами. При работе с машинной моделью всегда возможно прерывание эксперимента на время, необходимое для анализа результатов и принятия решений об его дальнейшем ходе (например, о необходимости изменения значений параметров модели).
Основные понятия процесса планирования экспериментов.Наиболее подходящей моделью этого процесса является абстрактная схема, называемая «черным ящиком». При таком подходе различают входные и выходные переменные: 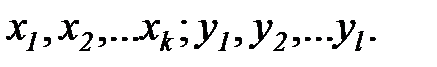 В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией. Пусть, например, имеют место только две переменные:
В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией. Пусть, например, имеют место только две переменные: 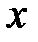 и
и 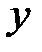 . Тогда если цель эксперимента - изучение влияния переменной х на переменную у, то х – фактор, а у – реакция. В экспериментах с машинными моделями системы фактор является управляемой (входной) переменной, а реакция – выходной переменной. Например, в агрегативной системе (A-схеме) факторами будут входные и управляющие сообщения, а реакциями – выходные.
. Тогда если цель эксперимента - изучение влияния переменной х на переменную у, то х – фактор, а у – реакция. В экспериментах с машинными моделями системы фактор является управляемой (входной) переменной, а реакция – выходной переменной. Например, в агрегативной системе (A-схеме) факторами будут входные и управляющие сообщения, а реакциями – выходные.
Каждый фактор 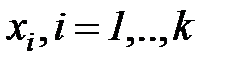 , может принимать в эксперименте одно из нескольких значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов.
, может принимать в эксперименте одно из нескольких значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов.
Каждому фиксированному набору уровней факторов соответствует определенная точка в многомерном пространстве, называемом факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как, например, это показано в разделе 7.2.4.
Существует вполне определенная связь между уровнями факторов и реакцией (откликом) системы, которую можно представить в виде соотношения
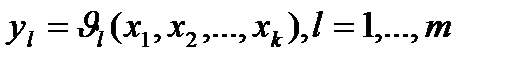
Функцию 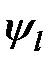 , связывающую реакцию с факторами, называют функцией реакции, а геометрический образ, соответствующий функции реакции,— поверхностью реакции. Исследователю заранее не известен вид зависимостей
, связывающую реакцию с факторами, называют функцией реакции, а геометрический образ, соответствующий функции реакции,— поверхностью реакции. Исследователю заранее не известен вид зависимостей 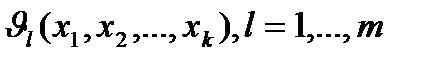 , поэтому используют гипотезы о виде этих зависимостей, дающих приближенные соотношения:
, поэтому используют гипотезы о виде этих зависимостей, дающих приближенные соотношения:
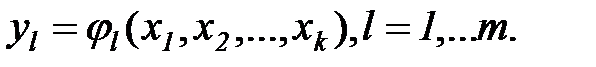
Зависимости 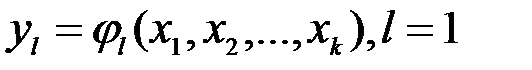 находятся по данным эксперимента, который необходимо поставить так, чтобы при минимальных затратах ресурсов (например, минимальном числе испытаний), варьируя по специально сформулированным правилам значения входных переменных, построить математическую модель системы и оценить ее характеристики.
находятся по данным эксперимента, который необходимо поставить так, чтобы при минимальных затратах ресурсов (например, минимальном числе испытаний), варьируя по специально сформулированным правилам значения входных переменных, построить математическую модель системы и оценить ее характеристики.
При планировании экспериментов необходимо определить основные свойства факторов. Факторы при проведении экспериментов могут быть управляемыми и неуправляемыми, наблюдаемыми и ненаблюдаемыми, изучаемыми и неизучаемыми, количественными и качественными, фиксированными и случайными.
Фактор называется управляемым, если его уровни целенаправленно выбираются исследователем в процессе эксперимента. При машинной реализации модели исследователь принимает решения, управляя их изменением в допустимых пределах различных факторов.
Фактор называется наблюдаемым, если его значения наблюдаются и регистрируются. Неуправляемый фактор также можно наблюдать. Например, на этапе проектирования конкретной системы нельзя управлять заданными воздействиями внешней среды, но можно генерировать их в машинном эксперименте. Наблюдаемые неуправляемые факторы получили название сопутствующих. Обычно при машинном эксперименте с моделью число сопутствующих факторов велико, поэтому рационально учитывать влияние лишь тех из них, которые наиболее существенно воздействуют на интересующую исследователя реакцию.
Фактор относится к изучаемым, если он включен в модель для изучения свойств системы, а не для вспомогательных целей, например для увеличения точности эксперимента.
Фактор будет количественным, если его значения — числовые величины, влияющие на реакцию, а в противном случае фактор называется качественным. Например, в модели системы, формализуемой в виде схемы массового обслуживания (Q)-схемы), количественными факторами являются интенсивности входящих потоков заявок, интенсивности потоков обслуживания, емкости накопителей, количество обслуживающих каналов и т. д., а качественными факторами — дисциплины постановки в очередь, выбора из очереди, обслуживания заявок каналами и т. д. Качественным факторам в отличие от количественных не соответствует числовая шкала. Однако и для них можно построить условную порядковую шкалу, с помощью которой производится кодирование, устанавливая соответствие между условиями качественного фактора и числами натурального ряда.
Фактор называется фиксированным, если в эксперименте исследуются не все интересующие экспериментатора значения фактора. Если экспериментатор исследует только некоторую случайную выборку из совокупности интересующих значений факторов, то фактор называется случайным. На основании случайных факторов могут быть сделаны вероятностные выводы и о тех значениях факторов, которые в эксперименте не исследовались.
В машинных экспериментах с моделями не бывает неуправляемых или ненаблюдаемых факторов применительно к исследуемой системе. В качестве воздействий внешней среды, т. е. неуправляемых и ненаблюдаемых факторов, в машинной имитационной модели выступают стохастические входные переменные.
Как уже отмечалось, каждый фактор может принимать в испытании одно или несколько значений, называемых уровнями, причем фактор будет управляемым, если его уровни целенаправленно выбираются экспериментатором. Для полного определения фактора необходимо указать последовательность операций, с помощью которых устанавливаются его конкретные уровни. Такое определение фактора называется операциональным, оно обеспечивает однозначность понимания фактора.
При планировании эксперимента обычно одновременно изменяются несколько факторов. Определим требования, которые предъявляются к совокупности факторов. Основные из них – совместимость и независимость. Совместимость факторов означает, что все их комбинации осуществимы, а независимость соответствует возможности установления фактора на любом уровне независимо от уровней других.
При проведении машинного эксперимента с моделью для оценки некоторых характеристик процесса функционирования исследуемой системы экспериментатор стремится создать такие условия, которые способствуют выявлению влияния факторов, находящихся в функциональной связи с искомой характеристикой. Для этого необходимо:
· отобрать факторы 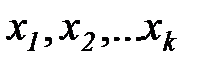 , влияющие на искомую характеристику, и описать вид функциональной зависимости;
, влияющие на искомую характеристику, и описать вид функциональной зависимости;
· установить диапазон изменения факторов;
· определить координаты точек факторного пространства, в которых следует проводить эксперимент;
· оценить необходимое число реализаций и их порядок в эксперименте.
Свойства объекта исследования можно описывать с помощью различных методов (моделей планирования). Для выбора конкретной модели необходимо сформулировать такие ее особенности, как адекватность, содержательность, простота и т.д. Под содержательностью модели планирования понимается ее способность объяснять множество уже известных фактов, выявлять новые и предсказывать их дальнейшее развитие. Простота – одно из главных достоинств модели планирования, выражающееся в реализуемости эксперимента на ЭВМ, но при этом может возникнуть противоречие с требованиями адекватности и содержательности.
Для описания функции отклика системы наибольшее применение нашли модели в виде алгебраических полиномов. Пусть изучается влияние к количественных факторов 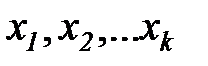 , на некоторую реакцию
, на некоторую реакцию 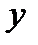 в отведенной для экспериментирования локальной области факторного пространства , ограниченной
в отведенной для экспериментирования локальной области факторного пространства , ограниченной 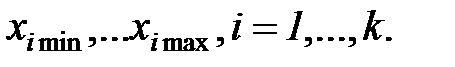 Обычно принимается гипотеза, что реакцию системы
Обычно принимается гипотеза, что реакцию системы 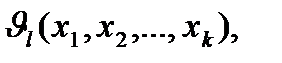 можно с некоторой степенью точности представить в виде аппроксимирующего полинома
можно с некоторой степенью точности представить в виде аппроксимирующего полинома 
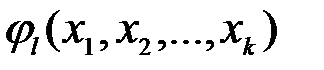 степени не выше d от к переменных
степени не выше d от к переменных
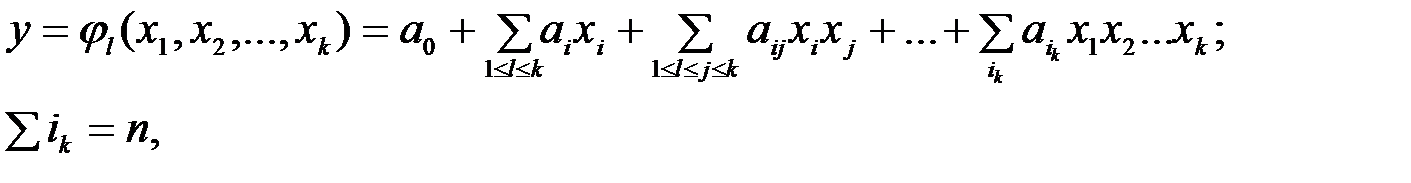 (7.1)
(7.1)
который содержит 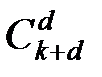 коэффициентов.
коэффициентов.
Ниже рассмотрен один из самых распространенных методов оценки параметров моделей по экспериментальным данным.
7.2 Построение моделей систем методами линейной регрессии
7.2.1 Метод наименьших квадратов - общая идея
Рассмотрим оценку параметров моделей вида (7.1) по известным экспериментальным данным. Строго говоря, для корректности последующих рассуждений необходимо предположение о нормальном распределении всех случайных величин, используемых для построения моделей.
Для дальнейшего изложения также существенно то, что модель линейна по параметрам 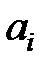 и
и 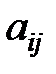 . Произведения переменных
. Произведения переменных 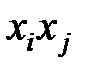 ,
, 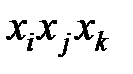 и т.д. можно рассматривать как новые переменные. Например, для модели второго порядка новые переменные можно ввести так:
и т.д. можно рассматривать как новые переменные. Например, для модели второго порядка новые переменные можно ввести так:
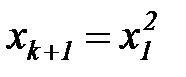 ,
, 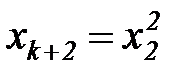 , … ,
, … , 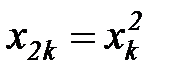 ,
, 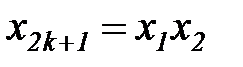 , … . (7.2)
, … . (7.2)
В итоге уравнение (6.1) будет приведено к простому линейному виду
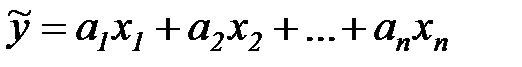 , (7.3)
, (7.3)
где 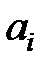 ,
, 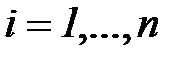 - неизвестные параметры,
- неизвестные параметры,
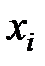 ,
, 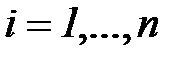 - входные переменные,
- входные переменные,
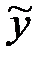 - выходная переменная, вычисленная по модели (7.3).
- выходная переменная, вычисленная по модели (7.3).
Предположим теперь, что имеется ряд наблюдений входных переменных 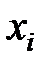 ,
, 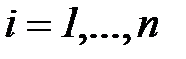 и выходной переменной
и выходной переменной 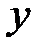 , сведенных в таблицу 7.1.
, сведенных в таблицу 7.1.
таблица 7.1
Таблица наблюдений
| Номер наблюдения | 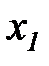
| 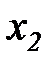
| 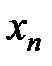
| 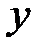
| |
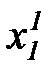
| 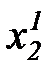
| … | 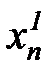
| 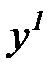
| |
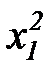
| 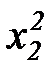
| … | 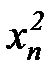
| 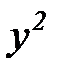
| |
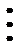
| … | … | … | … | … |
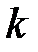
| 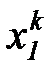
| 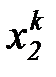
| … | 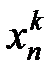
| 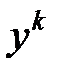
|
Здесь 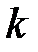 - число наблюдений (обычно
- число наблюдений (обычно 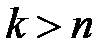 ),
), 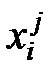 - значение переменной
- значение переменной 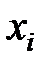 в j-м наблюдении,
в j-м наблюдении, 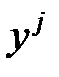 - значение выходной величины
- значение выходной величины 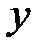 в j-м наблюдении.
в j-м наблюдении.
Поскольку экспериментальные значения 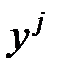 могут не совпадать с вычисленными
могут не совпадать с вычисленными 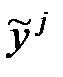 , то можно оценить невязку для
, то можно оценить невязку для  - го наблюдения
- го наблюдения
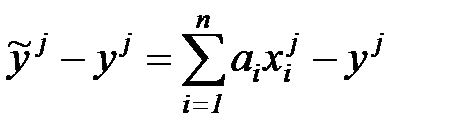 ,
,
а также общую невязку по всем наблюдениям:
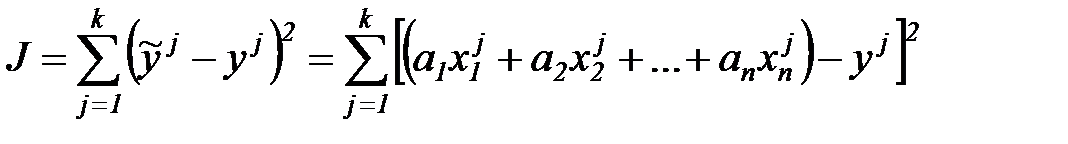 (7.4)
(7.4)
Для определения неизвестных 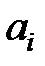 , минимизирующих невязку
, минимизирующих невязку
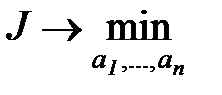 ,
,
потребуем выполнения 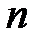 условий
условий
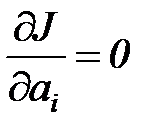 ,
, 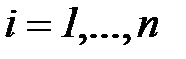 ,
,
откуда получим
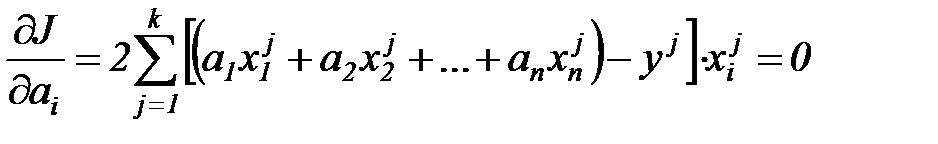 , (7.5)
, (7.5)
или после некоторого преобразования:
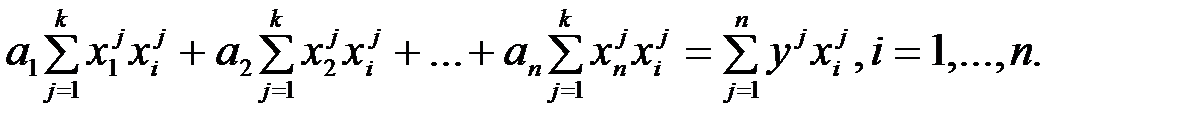 . (7.6)
. (7.6)
Вычислив все суммы по экспериментальным данным и решив полученную систему из 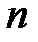 уравнений с
уравнений с 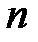 неизвестными (так называемую нормальную систему уравнений), получим регрессионную модель системы (7.3).
неизвестными (так называемую нормальную систему уравнений), получим регрессионную модель системы (7.3).
Описанная процедура носит название метода наименьших квадратов.
7.2.2 Метод наименьших квадратов в матричной форме
Представим совокупность параметров модели (7.3) в виде 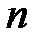 -вектора
-вектора
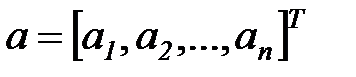 ,
,
множество наблюдений входных переменных в виде 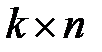 - матрицы
- матрицы
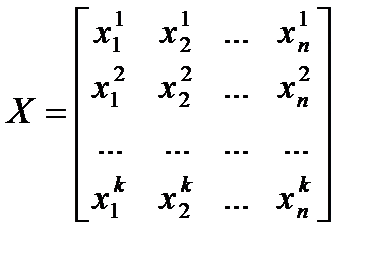 ,
,
множество наблюдений выходного параметра в виде 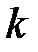 -вектора
-вектора
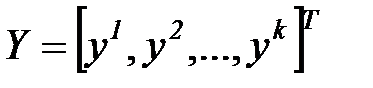 .
.
Тогда совокупность уравнений (7.3) для всех наблюдений может быть представлена в виде
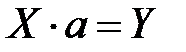 . (7.7)
. (7.7)
Умножив слева обе части уравнения (7.7) на транспонированную матрицу 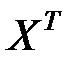 , получим
, получим
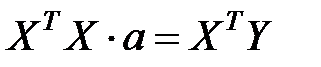 . (7.8)
. (7.8)
Нетрудно видеть, что 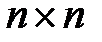 - матрица
- матрица 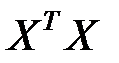 в (7.8) содержит все суммы, имеющиеся в левой части уравнения (7.6), а вектор
в (7.8) содержит все суммы, имеющиеся в левой части уравнения (7.6), а вектор 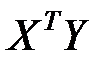 - все правые части этого уравнения. матрица
- все правые части этого уравнения. матрица 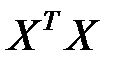 называется ковариационной матрицей экспериментальных данных. Таким образом, уравнение (7.8) представляет собой матричную запись уравнения (7.6). Умножив в (7.8) слева обе части на матрицу
называется ковариационной матрицей экспериментальных данных. Таким образом, уравнение (7.8) представляет собой матричную запись уравнения (7.6). Умножив в (7.8) слева обе части на матрицу 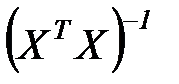 , получим формулу для вектора неизвестных параметров
, получим формулу для вектора неизвестных параметров
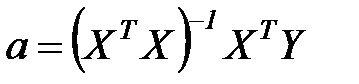 . (7.9)
. (7.9)
7.2.3 Центрирование и нормирование переменных
При практическом использовании уравнений (7.6) или (7.9) целесообразно привести все входные и выходные величины к единообразному безразмерному виду путем центрирования и нормирования переменных по формулам:
| (7.10) |
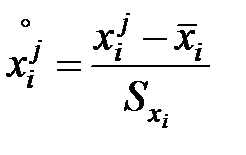 ,
, 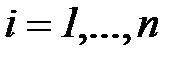 ,
, 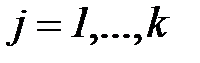 ,
,
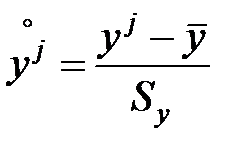 ,
, 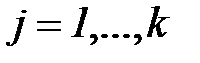 ,
,
где 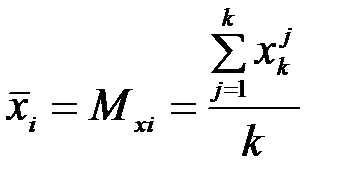 - среднее значение
- среднее значение 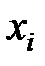 по всем наблюдениям,
по всем наблюдениям, 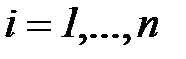 ,
,
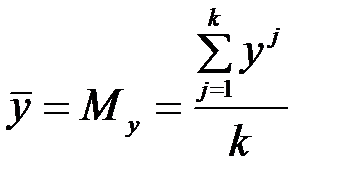 - среднее значение
- среднее значение 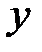 по всем наблюдениям,
по всем наблюдениям,
| (7.11) |
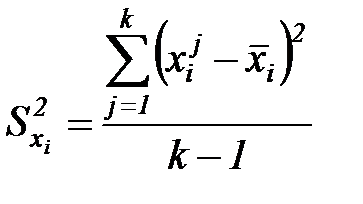 - дисперсия
- дисперсия 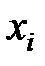 ,
, 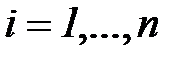 ,
,
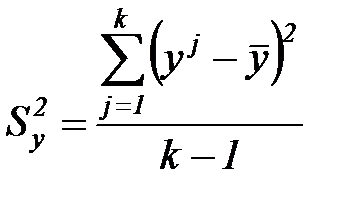 - дисперсия
- дисперсия 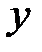 .
.
Обозначим матрицу, составленную из новых входных переменных:
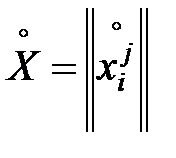 ,
, 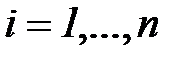 ,
, 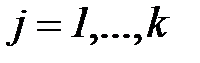 ,
,
вектор новых выходных переменных
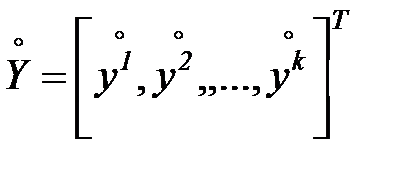 .
.
Тогда уравнение (7.9) примет вид
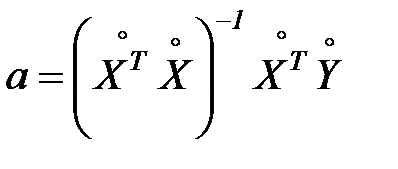 , (7.12)
, (7.12)
где
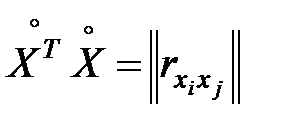 - матрица коэффициентов парной корреляции между переменными
- матрица коэффициентов парной корреляции между переменными 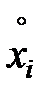
 и
и 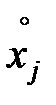 ,
,
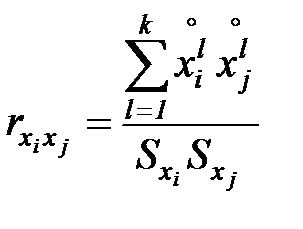 , (7.13)
, (7.13)
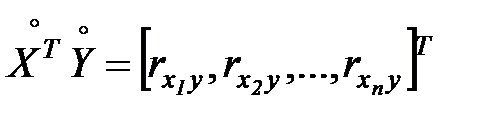 - (7.14)
- (7.14)
вектор коэффициентов парной корреляции между входными переменными 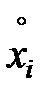 и выходной переменной
и выходной переменной 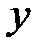 :
:
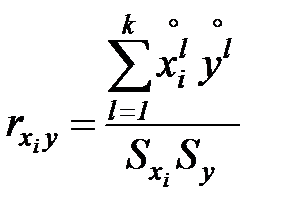 . (7.15)
. (7.15)
После вычисления вектора 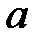 по формуле (7.12) необходимо вернуться к исходным переменным. В силу (7.3) и (7.12) уравнение регрессии имеет вид
по формуле (7.12) необходимо вернуться к исходным переменным. В силу (7.3) и (7.12) уравнение регрессии имеет вид
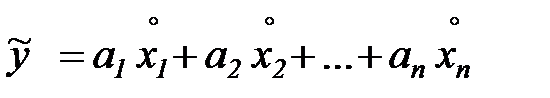 .
.
Подставив значения 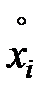 и
и 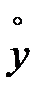 , вычисленные по формулам (7.10) получим
, вычисленные по формулам (7.10) получим
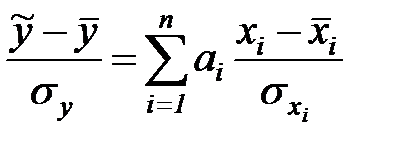 ,
,
откуда
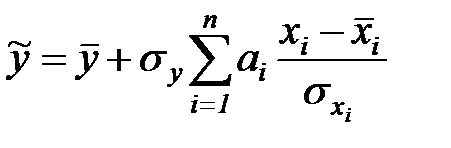 .
.
(7.16)
7.2.4 Метод наименьших квадратов при активном эксперименте
В тех случаях, когда имеется возможность влиять на ход эксперимента – выбирать значения входных переменных и наблюдать реакцию системы, вычисления могут значительно упрощаться. Одним из методов проведения активного эксперимента является полный факторный эксперимент. В этом случае все входные переменные варьируются на двух уровнях. При 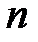 входных переменных получается
входных переменных получается 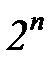 экспериментов.
экспериментов.
Пусть 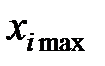 и
и 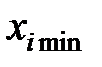 - соответственно наибольшее и наименьшее значение входного параметра
- соответственно наибольшее и наименьшее значение входного параметра 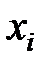 при проведении экспериментов. Введем безразмерные переменные
при проведении экспериментов. Введем безразмерные переменные
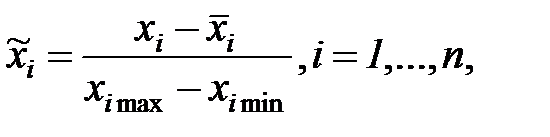 (7.17)
(7.17)
где 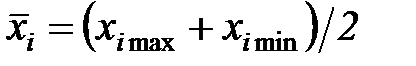 - средний уровень варьирования
- средний уровень варьирования 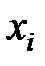 . Значения всех нормированных переменных
. Значения всех нормированных переменных 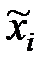 могут быть либо +1, либо –1.
могут быть либо +1, либо –1.
Рассмотрим для наглядности построение модели при активном эксперименте для случая 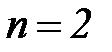 .
.
Уравнение регрессии в этом случае имеет вид
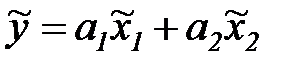 . (7.18)
. (7.18)
Составим таблицу эксперимента.
Таблица 7.2
Таблица активных экспериментов
| Номер эксперимента | 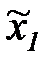
| 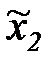
| 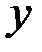
| |
| в десятичной системе | в двоичной системе | |||
| –1 | –1 | 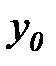
| ||
| –1 | 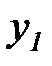
| |||
| –1 | 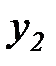
| |||
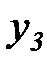
|
Правило составления таблицы 7.2 следующее. Номера всех 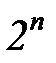 экспериментов выписываем в виде
экспериментов выписываем в виде 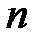 -разрядных двоичных чисел. Каждой переменной
-разрядных двоичных чисел. Каждой переменной 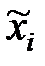 соответствует
соответствует 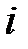 - й двоичный разряд
- й двоичный разряд 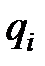 . При этом если
. При этом если 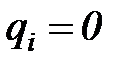 , то берется значение
, то берется значение 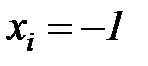 , а если
, а если 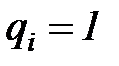 , то
, то 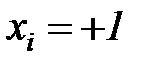 . В последнем столбце таблицы 6.2 для каждого эксперимента указано значение выходной переменной
. В последнем столбце таблицы 6.2 для каждого эксперимента указано значение выходной переменной 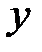 .
.
Воспользуемся формулой (7.9). Матрица 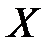 , в соответствии с таблицей примет вид
, в соответствии с таблицей примет вид
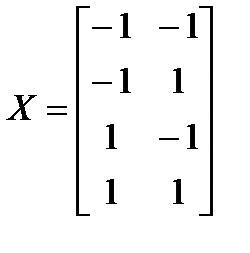 .
.
Остальные матрицы, входящие в (7.9), выглядят следующим образом:
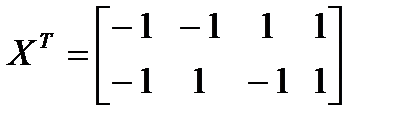 ;
; 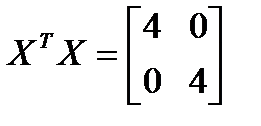 ;
; 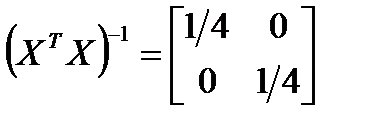 ;
;
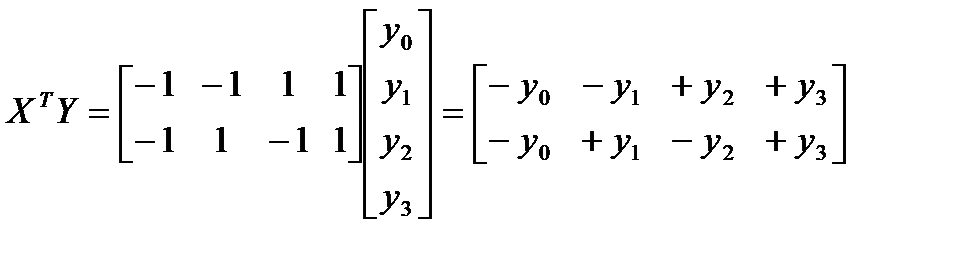 .
.
Обратим внимание на то, что ковариационная матрица 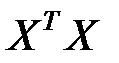 является диагональной. План эксперимента, при котором матрица
является диагональной. План эксперимента, при котором матрица 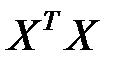 диагональная, называется ортогональным планом.
диагональная, называется ортогональным планом.
Параметры модели (7.16) определяются выражением
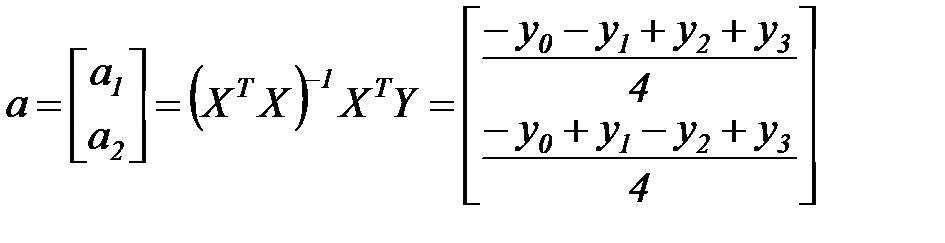 . (7.19)
. (7.19)
Вычислив вектор 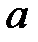 , следует возвратиться к исходным переменным. В силу (7.17) и (7.18) имеем следующую модель системы
, следует возвратиться к исходным переменным. В силу (7.17) и (7.18) имеем следующую модель системы
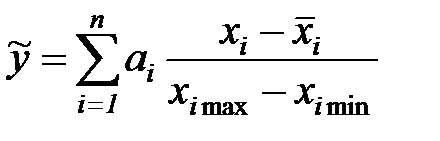 . (7.20)
. (7.20)
7.2.5 Оценка достоверности и качества регрессионных моделей
Рассмотрим оценку достоверности регрессионной модели в целом. Для этого в первую очередь необходимо вычислить так называемую остаточную дисперсию
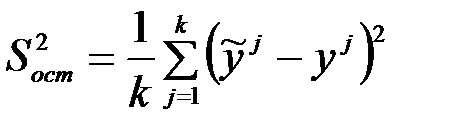 , (7.21)
, (7.21)
которая показывает суммарную невязку данных, вычисленных по модели и данных наблюдений. Выражение (7.21) пропорционально величине (7.4) при наилучшем выборе параметров  . Величину
. Величину 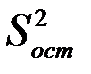 сравнивают с дисперсией выходной величины
сравнивают с дисперсией выходной величины 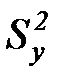 (формула 7.11).
(формула 7.11).
Отношение этих величин называют критерием Фишера:
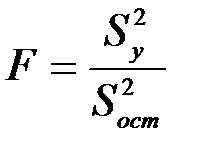 . (7.22)
. (7.22)
Чем больше эта величина, тем более точно модель соответствует экспериментальным данным. При заданных значениях 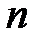 и
и 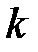 может быть получено табличное значение
может быть получено табличное значение 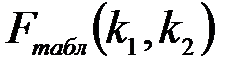 , где
, где 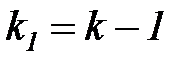 ,
, 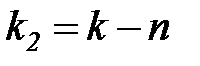 . Если
. Если 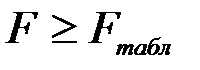 , то различие дисперсий считается существенным и использование уравнения регрессии имеет смысл. Если
, то различие дисперсий считается существенным и использование уравнения регрессии имеет смысл. Если 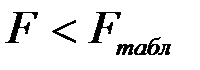 , то уравнение регрессии не имеет преимущества по сравнению с моделью
, то уравнение регрессии не имеет преимущества по сравнению с моделью 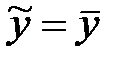 .
.
Другим показателем достоверности модели служит коэффициент множественной корреляции
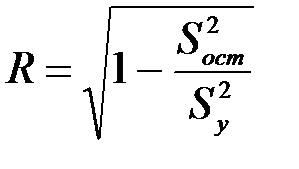 . (7.23)
. (7.23)
Рассмотрим теперь значимость коэффициентов корреляции между переменными, участвующими в построении модели.
Для оценки значимости коэффициентов корреляции 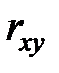 вычисляют среднюю квадратичную ошибку
вычисляют среднюю квадратичную ошибку
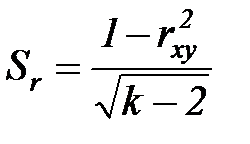 (7.24)
(7.24)
и отношение, называемое 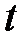 -критерием
-критерием
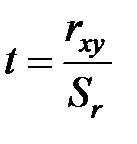 . (7.25)
. (7.25)
Эта величина сравнивается с табличным значением критерия Стьюдента 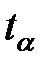 для
для 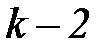 степеней свободы при доверительной вероятности
степеней свободы при доверительной вероятности 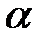 .
.
В инженерных расчетах обычно берется 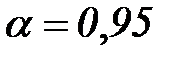 .
.
Для некоторых значений 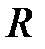 значения
значения 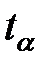 приведены в таблице 7.3.
приведены в таблице 7.3.
таблица 7.3
Значения 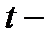 критерия и критических коэффициентов корреляции
критерия и критических коэффициентов корреляции
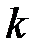
| ||||||||||
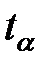
| - | 4.3 | 2.78 | 2.45 | 2.31 | 2.23 | 2.14 | 2.1 | 2.01 | 1.96 |
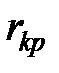
| 0.85 | -.7 | 0.62 | 0.56 | 0.52 | 0.46 | 0.41 | 0.27 | 0.06 |
Если при анализе модели получена величина 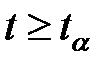 , то гипотеза о наличии значимой линейной связи между переменными
, то гипотеза о наличии значимой линейной связи между переменными 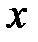 и
и 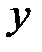 не отвергается, при
не отвергается, при 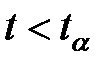 эта гипотеза отвергается. Поскольку величина
эта гипотеза отвергается. Поскольку величина 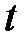 определяется коэффициентом корреляции
определяется коэффициентом корреляции 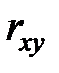 и числом
и числом 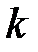 , то для каждого табличного значения
, то для каждого табличного значения 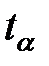 существует предельное значение
существует предельное значение 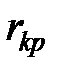 , которое также приведено в таблице 7.3. При этом соотношение
, которое также приведено в таблице 7.3. При этом соотношение 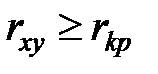 равносильно соотношению
равносильно соотношению 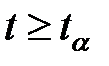 , а
, а 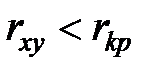 соответствует
соответствует 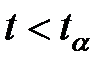 .
.
Этим же критерием можно пользоваться при оценке коэффициента множественной корреляции, оценивающего качество модели в целом. В этом случае
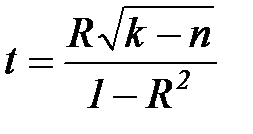 ,
,
а табличные значения 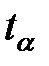 и
и 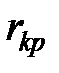 берутся из таблицы для числа степеней свободы равного
берутся из таблицы для числа степеней свободы равного 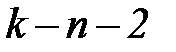 .
.
Оценим значимость переменных 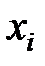 , входящих в модель. Рассмотрим матрицу парных коэффициентов корреляции (7.13)
, входящих в модель. Рассмотрим матрицу парных коэффициентов корреляции (7.13) 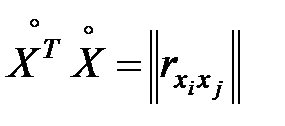 . Если коэффициенты
. Если коэффициенты 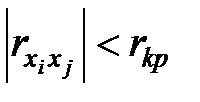 для данного числа наблюдений
для данного числа наблюдений 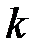 , то это говорит о независимости переменных
, то это говорит о независимости переменных 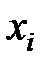 и
и 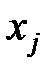 . Если же
. Если же 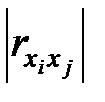 близок к единице, то это говорит об их взаимной зависимости, и одна из этих переменных является лишней, поскольку она не вносит вклада в модель.
близок к единице, то это говорит об их взаимной зависимости, и одна из этих переменных является лишней, поскольку она не вносит вклада в модель.
Рассмотрим вектор коэффициентов корреляции между входными величинами 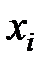 , и выходной величиной
, и выходной величиной 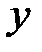 (7.14), (7.15)
(7.14), (7.15)
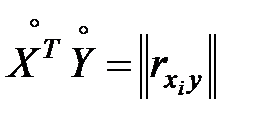 .
.
Если 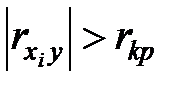 , то можно считать, что переменная
, то можно считать, что переменная 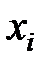 вносит существенный вклад в модель. Если же
вносит существенный вклад в модель. Если же 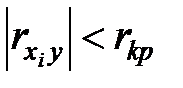 , то вклад переменной
, то вклад переменной 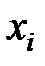 несущественный, и она может быть исключена из модели. Таким образом, процесс построения регрессионной модели носит итеративный характер. Сперва строится модель по всем выбранным переменным, оценивается коэффициент множественной корреляции
несущественный, и она может быть исключена из модели. Таким образом, процесс построения регрессионной модели носит итеративный характер. Сперва строится модель по всем выбранным переменным, оценивается коэффициент множественной корреляции 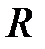 или
или 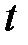 -критерий, на основе его анализа принимается решение об адекватности модели в целом. Затем производится уточнение влияния отдельных переменных
-критерий, на основе его анализа принимается решение об адекватности модели в целом. Затем производится уточнение влияния отдельных переменных 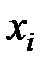 на выходную величину и друг на друга. Если какая-либо переменная исключается из модели, то пересчитываются параметры модели и величина
на выходную величину и друг на друга. Если какая-либо переменная исключается из модели, то пересчитываются параметры модели и величина 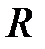 .
.
Дата добавления: 2016-06-13; просмотров: 1387;
