Абсолютная сходимость

Для рядов с произвольным распределением знаков рассмотрим следующий достаточный признак сходимости

Если ряд, составленный из абсолютных величин данного ряда, сходится, то сходится и данный ряд.

Доказательство

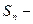сумма первых n элементов ряда;

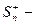сумма всех положительных среди первых n элементов ряда;

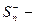сумма абсолютных величин всех отрицательных среди первых n элементов ряда;

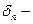сумма абсолютных величин всех первых n элементов ряда;

Тогда имеет место 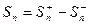и

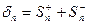
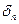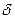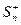Так как по условию имеет предел (обозначим ), а и 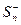- положительные и возрастающие функции от n, причем, 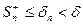и 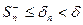, то они имеют пределы. Поэтому 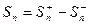при 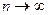стремится к пределу. Теорема доказана.

Это достаточный признак не является необходимым, то есть ряд 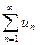может сходиться, а ряд 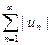- расходится.

Пример

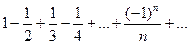- сходится

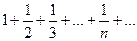- расходится (ряд из абсолютных величин - гармонический ряд)

Определение

Ряд, абсолютные величины элементов которого образуют сходящийся ряд, называется абсолютно сходящимся.

Если ряд сходится, а ряд образованный из абсолютных величин его элементов, расходится, то данный ряд называется условно сходящимся ( не абсолютно).

Например 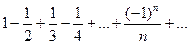- условно сходящийся.

Указанное разграничение абсолютной и условной сходимостей рядов является весьма существенным.

Оказывается, что некоторые свойства конечных сумм переносятся только на абсолютно сходящиеся ряды; условно сходящиеся этими свойствами не обладают.

Так абсолютно сходящиеся ряды обладают переместительным свойством (при любой перемене мест элементов абсолютно сходящихся рядов он остается абсолютно сходящимся и с той же суммой). Это свойство отсутствует у условно сходящихся рядов. Оказывается, переставляя элементы такого ряда, можно добиться того, что сумма ряда изменится.

Пример

Рассмотрим ряд 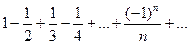и переставим элементы ряда таким образом

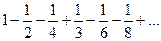Сложим каждый положительный элемент с идущим после него отрицательным: 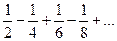В результате получим ряд, элементы которого образованы произведениями элементов исходного ряда на величину 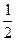. Но такой ряд по свойству 1 также сходится и его сумма равна 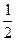суммы исходного ряда.

Абсолютно сходящиеся ряды можно перемножать

Определение

Под произведением двух сходящихзся рядов

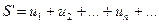(1)

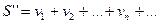(2)

Понимается следующий ряд

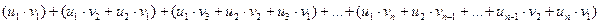(3)

В каждой группе элементов этого ряда, объединенных скобками, сумма индексов сомножителей постоянна: в первой – 2; во второй – 3; … ; в n – ой – (n+1)