Необходимый признак сходимости ряда. Гармонический ряд.
Если ряд сходится, то общий элемент стремится к нулю при возрастании его номера.
Доказательство
Имеем 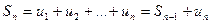 . Если ряд сходится, то
. Если ряд сходится, то 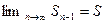 и
и 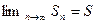 . Поскольку
. Поскольку 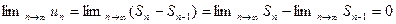
Из доказанного вытекает достаточный признак расходимости ряда.
Если 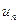 не стремится к нулю, то ряд не может быть сходящимся.
не стремится к нулю, то ряд не может быть сходящимся.
Пример
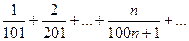 ряд расходится, так как
ряд расходится, так как 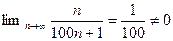
Следует помнить, что стремление n-го элемента к нулю не является достаточным для сходимости ряда.
Рассмотрим ряд 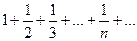 - гармонический ряд.
- гармонический ряд.
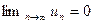 , но ряд расходится. Покажем, что
, но ряд расходится. Покажем, что 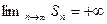 . Для доказательства заменим некоторые элементы ряда меньшими числами и убедимся, что даже сумма меньших слагаемых будет стремиться к бесконечности.
. Для доказательства заменим некоторые элементы ряда меньшими числами и убедимся, что даже сумма меньших слагаемых будет стремиться к бесконечности.
Сделаем разбиение ряда на группы
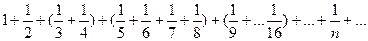
Следующая замена
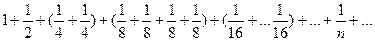 сумма каждой скобки равна
сумма каждой скобки равна 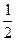 . Поскольку таких скобок можно брать сколько угодно, то сумма стремится к бесконечности.
. Поскольку таких скобок можно брать сколько угодно, то сумма стремится к бесконечности.
Таким образом, частичные суммы ряда неограниченно возрастают, следовательно, ряд расходится.
Пример
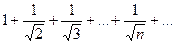 ряд расходится, так как даже при выполнении необходимого признака
ряд расходится, так как даже при выполнении необходимого признака 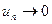 при
при 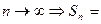
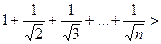
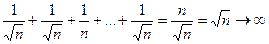
Дата добавления: 2016-11-22; просмотров: 704;
