Теорема ( без доказательства)

Если ряды (1) и (2) абсолютно сходятся, то их произведение есть также абсолютно сходящийся ряд, сумма которого равна произведению сумм рядов сомножителей

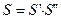
Функциональные ряды

Ряд, элементами которого являются функции, называется функциональным рядом.

Обозначение

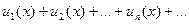(*) , где 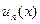- определены и непрерывны в одном и том же интервале.

Ряд (*) для одних значений х может сходиться, а для других расходиться.

Значение 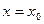, при котором числовой ряд 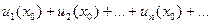сходится, называется точкой сходимости ряда (*).

Совокупность всех точек сходимости ряда называется областью сходимости ряда, или говорят, что ряд сходится в данной области. Обласью сходимости обычно бывает какой-либо интервал оси ОХ.

Пример

Ряд 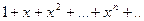сходится в интервале (-1;1), так как при |x|<1 – числовой ряд бесконечно убывающая геометрическая прогрессия.

При 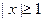- ряд расходится.

Сумма ряда является некоторой функцией от х, определенной в области сходимости ряда.

Обозначение

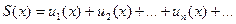
Для приведенного примера 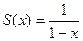, для интервала (-1;1), то есть области сходимости ряда.

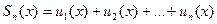- n –ая частичная сумма;

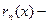остаток ряда.

Если ряд сходится, то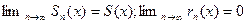

Известно, что сумма кончного числа непрерывных функций – функция непрерывная, и интеграл от такой суммы непрерывных функций равен сумме интегралов от этих функций. Точно также производная от суммы конечного числа дифференцируемых функций равна сумме производных.

Можно ли эти свойства перенести на функциональные ряды?

Покажем, что для произвольных функциональных рядов эти свойства могут оказаться несправедливыми.

Рассмотрим ряд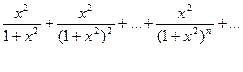

При х=0 элементы ряда нули и S(0)=0.

При 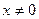- ряд сходящаяся геометрическая прогрессия, так как 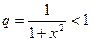и сумма ряда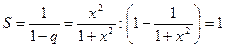

Таким образом, S(x) – разрывная функция. Она имеет разрыв в точке х=0, то есть S(x)=1, если 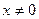и S(0)=0.

Чтобы установить, в каких же случаях на функциональные ряды можно перенести свойства конечных сумм, введем новое определение.

Определение

Функциональный ряд 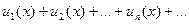(*) называется правильно сходящимся в области D, принадлежащей области сходимости ряда, если в области D все его элементы по абсолютной величине не превосходят соответствующих элементов некоторого числового ряда с положительными элементами.

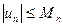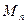Это значит, что во всех точках области D должно выполняться неравенство , где - элемент сходящегося ряда 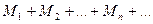Этот ряд называется мажорирующим (усиливающим) по отношению к ряду (*).

Пример

Ряд 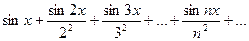правильно сходится в любом интервале оси ОХ, так как 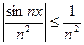, а ряд обратных квадратов сходящийся.