Знакочередующиеся ряды

Знакочередующийся ряд можно записать в таком виде:

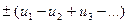(*), где 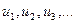- положительные числа.

Достаточный признак сходимости – признак Лейбница

Если в знакочередующемся ряду абсолютные величины элементов ряда убывают, то есть в ряде (*) 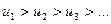и общий элемент 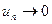, то ряд сходится, причем его сумма по абсолютной величине меньше 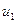; остаток ряда 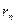по абсолютной величине меньше абсолютной величины первого из отбрасываемых элементов .

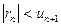Доказательство

Возьмем для определенности перед всем рядом (*) знак плюс

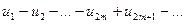
Рассмотрим сначала последовательность частичных сумм с четными индексами и запишем их в виде

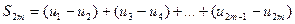
Так как по условию выражение в каждой скобке положительно и число таких скобок растет вместе с m, то последовательность 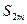будет возрастающей.

Наоборот, последовательность частичных сумм с нечетными индексами будет убывающей, так как

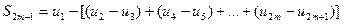и сумма в квадратной скобке, на основании только, что высказанных соображений, будет возрастать вместе с m.

Таким образом 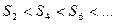и

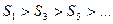
Легко заметить, что любая сумма с четным индексом меньше любой суммы с нечетным индексом:

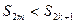
Действительно, если m<k, то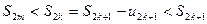

Если же 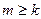, то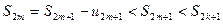

На следующем рисунке показано геометрическое изображение последовательности частичных сумм

Последовательность сумм с четными индексами возрастает и ограничена сверху: значит, она имеет предел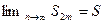

Так как 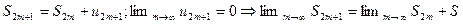, то есть суммы с нечетными индексами, убывая, стремятся к тому же пределу S.

На рисунке ясно видно, что частичные суммы, приближаясь к своему пределу, будут по очереди то больше его, то меньше: ясно также, что сумма ряда S меньше любой суммы с нечетным индексом и в частности меньше .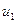

Если бы перед всем рядом (*) стоял знак минус, то рисунок надо было бы симметрично отобразить относительно начала координат: в этом случае было бы .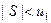

Остаток ряда 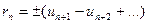представляет собой ряд, удовлетворяющий всем условиям признака Лейбница. Поэтому сумма 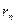по абсолютной величине меньше первого элемента в скобке, то есть 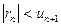. Теорема доказана.

Пример

Ряд 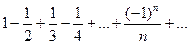сходится, так как он удовлетворяет всем условиям признака Лейбница.