Ряды с положительными элементами. Достаточные признаки сходимости.

1. Признаки сравнения

Рассмотрим ряд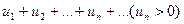

Лемма Если частичные суммы ряда с положительными элементами ограничены сверху, то ряд сходится. (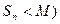

Доказательство

Так как 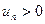, то частичные суммы ряда по мере возрастания числа элементов тоже возрастают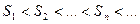

Но если последовательность монотонно возрастает и ограничена сверху, то по признаку Вейерштрасса она имеет предел, также не превосходящий числа М. Следовательно, имеем 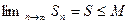. Верно обратное. Если ряд с положительными элементами сходится, то его частичные суммы меньше суммы ряда: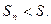

Замечание

Если ряд с положительными элементами расходится, то его частичные суммы стремятся к бесконечности, то есть 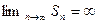или другая запись .

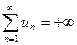Признак сравнения

Пусть даны два ряда с положительными элементами:

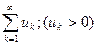(1) и 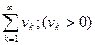(2) и пусть каждый элемент ряда (1) не больше соответствующего элемента ряда (2) 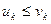(*). Тогда

1) Если сходится ряд (2), то сходится и ряд (1)

2) Если расходится ряд (1), то расходится и ряд (2)

Доказательство

Докажем первую часть теоремы. Полагаем ,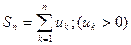

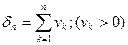
По условию ряд (2) сходится, поэтому 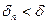, где 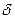- сумма ряда (2). А из условия (*) следует, что 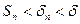. Получаем, что частичные суммы ряда (1) ограничены сверху. В силу доказанной выше леммы ряд (1) сходится.

Для доказательства второй части достаточно заметить, что, поскольку ряд (1) расходится, то его суммы неограниченно возрастают: .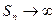

Так как 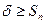, то и 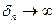. Следовательно ряд (2) расходится.

Признаки сравнения применимы и в том случае, когда условию (*) удовлетворяют элементы ряда не при всех n, а лишь начиная с некоторого n=N. Это следует из третьего свойства сходящихся рядов.

Примеры:

1. Ряд 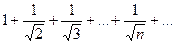расходится, так как гармонический ряд 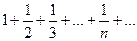расходится, а 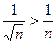при n>1

2. Ряд 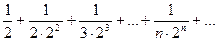сходится, так как сходится ряд 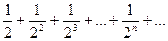(убывающая геометрическая прогрессия) и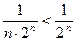

Замечание

На практике признаки сравнения наиболее удобно применять в следующем виде:

Если 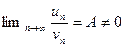, то ряды (1) и (2) или оба сходятся, или оба расходятся.

Доказательство

Из определения предела следует, что для всякого 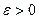можно указать такое число N, что при всех n>N будет справедливо неравенство 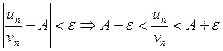, где 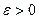настолько мало, что .

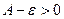Предположим сначала, что ряд (2) сходится. Тогда по свойству (1) сходится и ряд с общим элементом 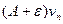и по признаку сравнения сходится ряд (1), так как .

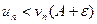Наоборот, если ряд (2) расходится, то из неравенства 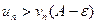будет следовать, что расходится ряд (1).

Пример: Ряд 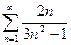расходится, так как, выбирая 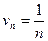- гармонический ряд и вычисляем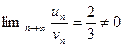

В качестве эталонов для сравнения рядов выбирают: гармонический ряд – расходящийся; бесконечно убывающая геометрическая прогрессия или ряд обратных квадратов – сходящиеся.

Признак Даламбера

Рассмотрим ряд (*)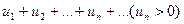

Если при 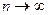существует предел отношения последующего элемента к предыдущему, то есть 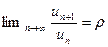, то при

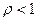- ряд сходится; 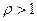- ряд расходится; 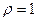- признак Даламбера не действует.

Доказательство

Пусть 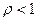. В силу определения предела всегда можно выбрать такое число N. Что при всех 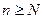будет справедливо неравенство

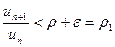, где 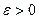берется настолько малым, что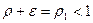

Тогда 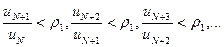получаем неравенства

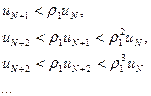
Отсюда вытекает, что элементы ряда 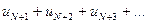представляющего N-ый остаток данного ряда, меньше соответствующих элементов бесконечно убывающей геометрической прогрессии

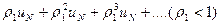
Следовательно N-ый остаток ряда сходится, тогда сходится и сам ряд.

Пусть 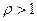.В силу определения предела всегда можно выбрать такое число N. Что при всех 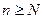будет справедливо неравенство

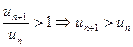
Но тогда каждый последующий элемент ряда будет больше предшествующего и, поскольку все они положительны, не может выполняться необходимый признак сходимости ряда, согласно которому общий элемент должен стремиться к нулю, то есть ряд расходится.

Примеры

1. Ряд 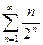сходится, так как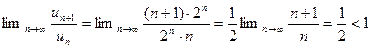

2. Рассмотрим ряд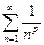

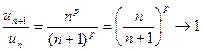при 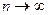независимо от величины показателя p.

При p=1 – гармонический ряд (расходится);

При p=2 – ряд обратных квадратов (сходится).

Следовательно, при 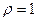- признак Даламбера не действует.