Интегральный признак Коши

Не трудно заметить полную аналогию определений сходимости ряда и сходимости несобственного интеграла с бесконечным верхним пределом. Много общего и в признаках сходимости рядов с положительными элементами и интегралов с положительной подынтегральной функцией.

Рассмотрим признак, позволяющий в некоторых случаях сводить вопрос о сходимости ряда, к вопросу о сходимости интеграла.

Рассмотрим ряд 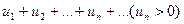(*), элементы которого являются значениями непрерывной положительной функции f(x) при целых значениях аргумента х:

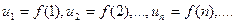и пусть f(x) монотонно убывает в интервале 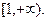Тогда ряд сходится, если сходится несобственный интеграл 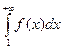и расходится, если этот интеграл расходится.

Доказательство

Рассмотрим криволинейную трапецию, ограниченную линией y=f(x), с основанием от x=1 до x=n, где n – произвольное положительное число. (см. Рис.). Площадь измеряется интегралом

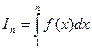
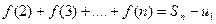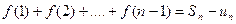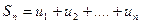Отметим точки основания x=1, x=2, ….,x=n. Рассмотрим две ступенчатые фигуры. Одна из них (входящая) имеет площадь равную , а вторая (выходящая) – площадь равную , где . Для представленных площадей справедливо 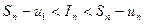. Отсюда получаем два неравенства:

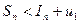(1)

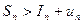(2)

Так как f(x)>0, то 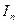возрастает вместе с n. Возможны два случая:

1) Несобственный интеграл сходится, то есть 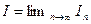существует, тогда 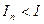и из неравенства (1) при всяком n находим 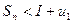, то есть 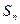- ограничена, тогда на основании леммы ряд сходится.

2) Интеграл расходится: тогда 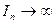при 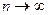и на основании неравенства (2) следует, что 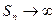, то есть ряд расходится.

Пример

Рассмотрим ряд 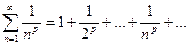. Для этого ряда признак Даламбера не применим, так как .

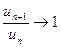Применим интегральный признак. Подынтегральная функция 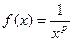. Соответственно интеграл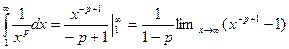

Если p>1, то 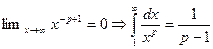- интеграл сходится.

Если p<1, то интеграл расходится, так как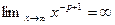

При p=1 интеграл также расходится: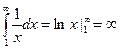

В итоге получаем:

При p>1 – ряд сходится

При p<1 – ряд расходится

Геометрическую идею, лежащую в основе доказательства интегрального признака Коши, можно применить для оценки ошибки, возникающей при приближенном вычислении суммы ряда, сходимость которого была установлена с помощью этого признака. Для этого нужно уметь оценивать величину разности

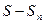, то есть остаток ряда 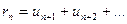. 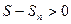при любом n.

Приведенный рисунок показывает, что остаток ряда есть сумма “уходящих вправо” прямоугольников и она меньше, чем площадь заключающей их фигуры, поэтому

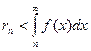
Применим эту формулу для лценки остатка только, что рассмотренного ряда 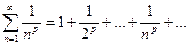при p>1

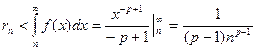
Если необходимо, чтобы величина остатка ряда не превышала заранее выбранного числа 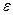, то за номер n можно взять наименьшее целое число , удовлетворяющее неравенству

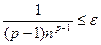
Пусть 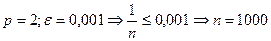- это медленно сходящийся ряд.

Пусть 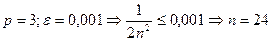- это ряд обратных кубов.

Пусть 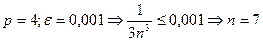- быстро сходящийся ряд.