Свойства правильно сходящихся рядов

Сформулируем основные теоремы о правильно сходящихся рядах, которые дают ответ на вопрос о переносе на ряды свойств сумм конечного числа функций. Во всех теоремах предполагается, что область правильной сходимости ряда есть некоторый интервал оси ОХ.

Теорема 1

Если ряд из непрерывных функций правильно сходится в области D, то его сумма есть функция непрерывная в этой области.

Так ряд 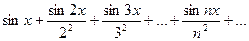сходится правильно в любом интервале. Следовательно, его сумма S(x) – непрерывная функция.

Теорема 2

Если ряд из непрерывных функций правильно сходится, то интеграл от суммы ряда равен сумме ряда, сотавленного из интегралов от этих функций:

(*)

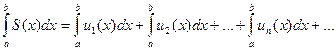Короткая формулировка

Правильно сходящийся ряд можно поэлементно интегрировать

Доказательство

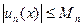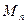Из определения правильной сходимости данного ряда следует, что , где - элемент сходящегося числового ряда. По теореме об оценке интегралов, имеем

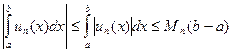
Но ряд с общим элементом 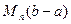сходится, тогда сходится и ряд из интегралов и даже абсолютно.

Замечание

Теорема 2 справедлива и в том случае, когда берутся интегралы с переменным верхним пределом

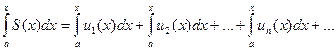где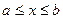

Пользуясь оценкой интегралов, имеем 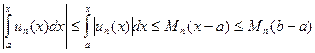. Тогда и данный ряд сходится правильно.

Теорема 3

Если ряд 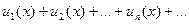составленный из функций, имеющих непрерывные производные, сходится в области D и его сумма равна S(x), а ряд из производных 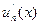сходится в этой области правильно, то производная суммы ряда S’(x) равна сумме ряда из производных

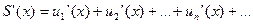
Короткая формулировка

Если ряд, составленный из производных сходящегося ряда, сходится правильно, то его можно поэлементно дифференцировать.

Замечание

Правильная сходимость данного ряда, а также дифференцируемость его суммы не предполагается, а является следствиеми условий теоремы. Однако проверка правильной сходимости ряда из производных совершенно обязательна; при невыполнении этого условия теорема может потерять смысл.

Пример

Ряд 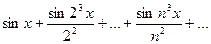правильно сходится (он мажорируется рядом обратных квадратов) и его сумма непрерывная функция.

Ряд из производных

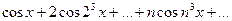расходится, так как его общий элемент ни при каком х не стремится к нулю. Следовательно теорем не применима.