Лапластың түрлендіруін өтпелі процестерді есептеуге қолдану және жіктеу теоремасы
Өтпелі процестерді классикалық әдіспен есептеу басты жағдай бойынша интегралдаудың тұрақтыларын белгілеу және басты функцияларды және олардың туындыларын табу үшін алгебралық теңдеулердің жүйесін дүркін-дүркін шешуді талап етеді. Бұл жағдай осы әдіспен есептеудің негізгі қиыншылығына жатады. Электр сүлбелер қүрделендірген сайын және дифференциялды теңдеудің дәрежесі өскен сайын бұл қиыншылықтарда өседі.
Сондықтан, тапсырылған басты жағдайлар бастапқы теңдеулерге кіргізіліп сызықты дифференциалды теңдеулерді шешу әдісті пайдалану қолайлы болады, өйткені бұл әдісте керекті функцияларды табу үшін интегралдаудың тұрақтыларын белгілеудің қажеттігі жоқ болады.
Сызықты дифференциалды теңдеулерді Лапластың түрлендірулерге негізделген операторлық әдіспен интегралдауға болады.
Операторлық әдістің маңызы – тұп нұсқа деп аталатын кейбір тапсырылған бір қатарлы шектелген заттың айнымалының 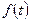 функциясына басқа бейнесі деп аталатын
функциясына басқа бейнесі деп аталатын 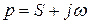 комплексті айнымалының
комплексті айнымалының 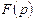 функциясы салыстырылады. Функция
функциясы салыстырылады. Функция 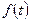 әрбір ақырғы уақыт аралықта Дирихле жағдайына қамтамасыз ету керек және
әрбір ақырғы уақыт аралықта Дирихле жағдайына қамтамасыз ету керек және 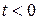 кезде нөлге тең болу керек.
кезде нөлге тең болу керек.
Салыстыру мына формула бойынша өткізіледі
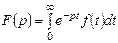
Бұл кейіптемеде - 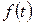 функцияның үстінен Лапластың тікелей түрлендіруін көрсетеді.
функцияның үстінен Лапластың тікелей түрлендіруін көрсетеді.
Оны былай белгілейді:
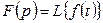 немесе
немесе 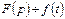 , мұнда
, мұнда 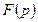 -
- 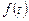 функцияның Лапластық бейнесі. Кері, егерде
функцияның Лапластық бейнесі. Кері, егерде 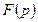 бейнесі бойынша
бейнесі бойынша 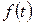 түп нұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады
түп нұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады

яғни бірінші интегралды теңдеуді 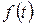 функцияға қатысты шешу.
функцияға қатысты шешу.
екінші интегралды былай белгілеугенде болады:
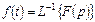 немесе
немесе 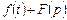 .
.
Тұп нұсқадан туындылардың және интегралдардың бейнелері үшін кейіптемелерін (шығарусыз) келтірейік:
Егер де 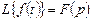 болса, онда
болса, онда
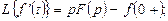
 және т.с.с.
және т.с.с.
Егер де 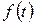 функция және оның туындылары
функция және оның туындылары 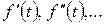
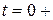 кезде кенет өзгерсе, онда (7.4) және (7.5) кейітемелерге олардың мәнін осы кенет өзгерісті есепке алып қою керек яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де
кезде кенет өзгерсе, онда (7.4) және (7.5) кейітемелерге олардың мәнін осы кенет өзгерісті есепке алып қою керек яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де 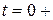 кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың бейнелері өте жеңіл табылады:
кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың бейнелері өте жеңіл табылады:
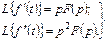 және т.с.с.
және т.с.с.
Тұп нұсқаудың интегралдық бейнелерінің түрі:

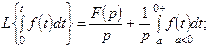
Егерде интеграл 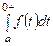
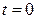 кезде кенет өзгерсе, онда оның мәнін нөлдік оң жағынан алу керек, бұл жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
кезде кенет өзгерсе, онда оның мәнін нөлдік оң жағынан алу керек, бұл жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
Бейне 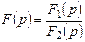 дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ.
дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ. 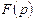 функцияның полюстерінің орыны
функцияның полюстерінің орыны 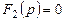 теңдеудің түбірлерімен белгіленеді. Бұл теңдеудің
теңдеудің түбірлерімен белгіленеді. Бұл теңдеудің 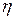 түбірлерін
түбірлерін 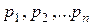 деп белгілейміз.
деп белгілейміз.
Екі жағдай болуға мүмкін:
а) барлық түбірлер жай;
б) кейбір немесе барлық түбірлер еселі.
а) жай түбірлердің жағдайы
Өте жай жағдайда бейне радионалды бөлшек түрде болады:

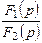 бөлшек қысқарылмайды, яғни
бөлшек қысқарылмайды, яғни 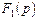 және
және 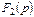 мүшелердің жалпы түбірлері жоқ, ал
мүшелердің жалпы түбірлері жоқ, ал 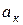 және
және 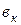 - заттық сандар. Бірінші бейненің түп нұсқасын жікте теормасы деп аталатын кейіптеме бойынша табуға болады:
- заттық сандар. Бірінші бейненің түп нұсқасын жікте теормасы деп аталатын кейіптеме бойынша табуға болады:
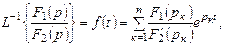
Мұнда pк сипаттамалы теңдеудің, яғни 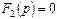 теңдеудің жай түбірлері, бір түбір нөлге тең болуы мүмкін.
теңдеудің жай түбірлері, бір түбір нөлге тең болуы мүмкін.
Егер де бір түбір нөлге тең болса, яғни бөлгіш ішінде р көбейткіш бар болса, онда жіктеу теореманың басқа түрі қолданады.

б) еселі түбірлердің жағдайы
Егер де көп мүшелі 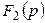 түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы ұқсасты жасауға болады, бірақ оң жағында қосындымен (бір қосынды түбірлер саны бойынша, ал екінші әрбір түбір үшін оның еселік реттігімен).
түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы ұқсасты жасауға болады, бірақ оң жағында қосындымен (бір қосынды түбірлер саны бойынша, ал екінші әрбір түбір үшін оның еселік реттігімен).
Сонымен, 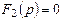 теңдеуде еселі түбірлер болса, онда
теңдеуде еселі түбірлер болса, онда 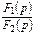 кесінді бойынша тұп нұсқау мына формула бойынша есептеледі:
кесінді бойынша тұп нұсқау мына формула бойынша есептеледі:
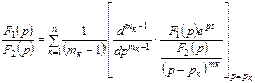
Шаршы жақшаның бөлгішіндегі көріністі алдымен 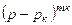 шамаға қысқартып, содан кейін дифференциялдау керек.
шамаға қысқартып, содан кейін дифференциялдау керек.
Дата добавления: 2017-01-29; просмотров: 2123;
