Основные утверждения о рядах Тейлора.

1º. Если степенной ряд 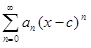сходится к функции f (x) на интервале ]c−R, c+R[ , R > 0, то он является рядом Тейлора для функции f (x).

Доказательство. По условию,

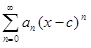= f(x), x ]c−R, c+R[ .

Степенной ряд можно почленно дифференцировать внутри интервала сходимости сколь угодно много раз. Следовательно, имеем следующие равенства:

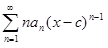= f ′(x),

= f ″(x),

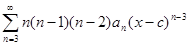= f ′″(x),

…………………………………………..

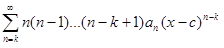= f ^(k)(x),

…………………………………………………

Тогда при x = c получим соотношения:

a₀ = f(c), 1∙ a₁ = f ′(c),2∙1∙ a₂ = f ″(c),3∙2∙1∙ a₃ = f ″′(c), ...,

k(k −1) ∙...∙2∙1∙ a_k = f ^(k)(c), ...

Отсюда

a₀ = f(c), a₁ = 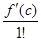, a₂ = 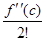, a₃ = 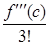, ..., a_k = , ....

Это означает, что степенной ряд 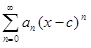является рядом Тейлора для функции f (x).

2º. Ряд Тейлора для функции f (x) не обязан сходится к самой функции f (x).

Для доказательства рассмотрим функцию

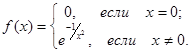
Если x ≠ 0, то

, , , ...

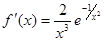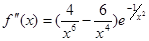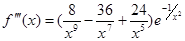В общем случае, при x ≠ 0

f ⁽ⁿ⁾(x) = ,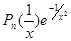

где P_n(z) − некоторый многочлен относительно z = .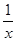

Покажем, что f ⁽ⁿ⁾(0) = 0, при n = 0,1,2,3, ...

В самом деле, f (0) = 0.

f ′(0) =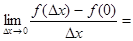

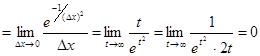, где .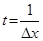

Предположим, что равенство f ⁽ⁿ⁾(0) = 0 уже доказано. Тогда

f ⁽ⁿ⁺¹⁾(0) =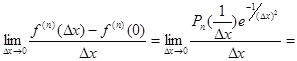

.

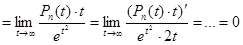Таким образом, ряд Маклорена для функции f(x) имеет вид:

0 + 0∙x + 0∙x² + ... + 0∙xⁿ + ... = 0, x ]−∞, +∞[ .

Однако, функция

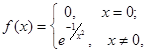
принимает ненулевые значения на любом интервале. Следовательно, не существует интервала, на котором ряд Маклорена для функции f (x) сходится к этой функции.

3º. Предположим, что функция f (x) дифференцируема на интервале ]x₀−∆, x₀+∆[ сколь угодно много раз. Ряд Тейлора для функции f (x) сходится на интервале ]x₀−∆, x₀+∆[ к самой функции f (x) тогда и только тогда, когда

= 0, x ]x₀−∆, x₀+∆[.

Доказательство. Интегрируя «по частям», получим:

=

= + =

= + =

= + + + =

= − + + = …

……= − − ….− − + =

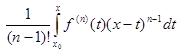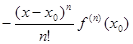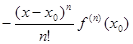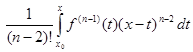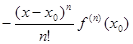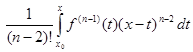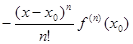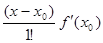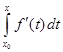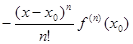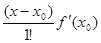= − − ….− − + f(x) − f(x₀).

Следовательно,

f (x) = f (x₀) + + ... + + + 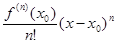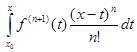, x ]x₀−∆, x₀+∆[.

Положим

S_n(x) = f (x₀) + + ... + 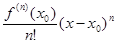, n N.

Тогда

f (x) = S_n(x) + 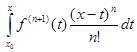, x ]x₀−∆, x₀+∆[, n N.

Отсюда 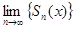= f (x) для любого x ]x₀−∆, x₀+∆[ тогда и только тогда, когда

= 0, x ]x₀−∆, x₀+∆[ .

Следствие. Пусть функция f (x) дифференцируема сколь угодно много раз на интервале ]x₀−∆, x₀+∆[ , ∆ > 0. Если существует число М > 0 такое, что 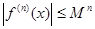для любого x ]x₀−∆, x₀+∆[, n N, то ряд Тейлора для функции f (x) сходится к самой функции f (x) на интервале ]x₀−∆, x₀+∆[.

Доказательство. Достаточно показать, что

= 0, x ]x₀−∆, x₀+∆[ .

Для этого заметим, что

≤ ≤ M ⁿ⁺¹∙ .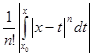

Если x > x₀, то

= = = .

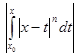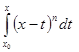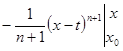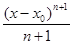Если же x < x₀, то

= = = =

= .

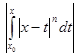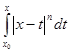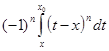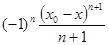
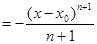Следовательно,

≤ ≤

≤ = .

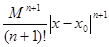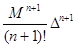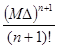Так как 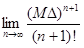= 0, то = 0 для каждого x ]x₀−∆, x₀+∆[.

Пример. Функция f (x) = sin x дифференцируема сколь угодно много раз на всей числовой прямой, причём

f ⁽ⁿ⁾(x) = .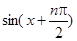

Тогда |f ⁽ⁿ⁾(x)| ≤ 1, x ]−∞, +∞[, n N.

Следовательно, ряд Маклорена для функции f (x) = sin x

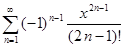
сходится на всей числовой прямой к самой функции f (x) = sin x. Таким образом,

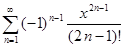= sin x, где x ]−∞, +∞[.

Точно также можно показать, что

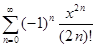= cos x, где x ]−∞, +∞[.

Задачи.

14.1. Составить ряд Маклорена для функции f (x) и найти область сходимости ряда:

а) f (x) = (1+x)ⁿ, n N; б) f (x) = ;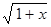

в) f (x) = 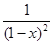; г) f (x) = sin2x;

д) f (x) = 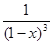; е) f (x) = ln(1− x).

14.2. Составить ряд Тейлора для функции f (x) и найти область сходимости ряда:

а) f (x) = 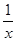, x₀ = 1; б) f (x) = ln x, x₀ = 1;

в) f (x) = e^x, x₀ = − 1; г) f (x) = 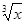, x₀ = 8;

д) f (x) = cos x, x₀ = ; е) f (x) =sin⁴ x, x₀ = .

14.3. Доказать, что ряд Маклорена для функции f (x) = e^x сходится к этой функции на всей числовой прямой.