Приближенные вычисления с помощью рядов
Функциональные ряды используются для приближенных вычислений. В частности, с помощью рядов можно:
· находить значения функций;
· вычислять интегралы;
· решать дифференциальные уравнения.
1.Приближенные вычисления значений функций
Чтобы вычислить значение функции f (x) в точке x = x*, можно поступить следующим образом:
· выбрать точку x0 вблизи точки x*;
· разложить функцию f (x) в ряд по степеням (x − x0) и найти область сходимости ряда;
· если точка x* попадёт в область сходимости ряда, то положить
f (x*) ≈ f (x0) + 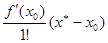 + ... +
+ ... +  . (16.1)
. (16.1)
Замечание. Количество слагаемых в равенстве (16.1) необходимо выбрать так, чтобы обеспечить требуемую точность δ, т.е. должно выполняться следующее условие
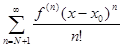 < δ.
< δ.
Пример.Вычислим ln3 с точностью до 0,001. Заметим, что ln3 =  и разложим функцию f (x) =
и разложим функцию f (x) = 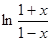 в ряд по степеням x. Получим
в ряд по степеням x. Получим
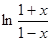 =
= 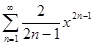 , x
, x  ]−1,1[
]−1,1[
(см. пример 2, разд. 15). Тогда
ln3 = 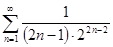 .
.
Следовательно,
ln3 ≈ 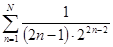
с точностью до 0,001, если RN +1 =  < 0,001.
< 0,001.
Остаток числового ряда RN +1 можно оценить сверху следующим образом:
RN +1 = 
 .
.
Следовательно, при N = 4 получим:
R5 ≤ 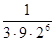 =
=  < 0,001.
< 0,001.
Тогда, с точностью до 0,001
ln3 ≈ 1 +  +
+ 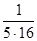 +
+ 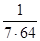 = 1,098065
= 1,098065
(точное значение: ln3 = 1,098612).
2.Приближенные вычисления интегралов
Для вычисления интеграла  разложим подынтегральную функцию f (x) в ряд по степеням (x − x0):
разложим подынтегральную функцию f (x) в ряд по степеням (x − x0):
f (x) = 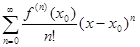 (16.2)
(16.2)
и найдем область сходимости ряда (16.2). Если z принадлежит области сходимости ряда, то ряд можно проинтегрировать почленно на отрезке [x0, z]. Получим
 =
= 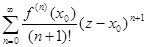 .
.
Тогда
 ≈
≈ 
с требуемой точностью δ, если RN +1 = 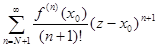 < δ.
< δ.
Пример. Вычислить с точностью до 0,001 интеграл
 .
.
Так как ex =  , x
, x  ]−∞, +∞[ , то
]−∞, +∞[ , то
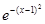 =
= 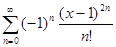 , x
, x  ]−∞, +∞[ .
]−∞, +∞[ .
Следовательно,
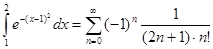 .
.
Числовой ряд 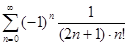 удовлетворяет всем условиям теоремы Лейбница. Следовательно,
удовлетворяет всем условиям теоремы Лейбница. Следовательно,
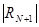 =
= 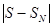 < aN +1 =
< aN +1 =  .
.
При N = 4 получим
 <
< 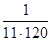 < 0,001.
< 0,001.
Тогда, с точностью до 0,001
 ≈ 1 −
≈ 1 − 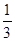 +
+ 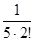 −
− 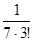 +
+  = 0,74749.
= 0,74749.
3.Решение дифференциальных уравнений
Рассмотрим дифференциальное уравнение первого порядка:
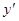 = f (x, y), (16.3)
= f (x, y), (16.3)
где y = y (x) − неизвестная функция, а 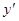 − её производная.
− её производная.
Функция φ(x) является решением дифференциального уравнения (16.3) на интервале ]a, b[, если выполняются следующие условия: функция φ(x) дифференцируема на интервале ]a, b[; для любого x  ]a, b[ имеет место равенство:
]a, b[ имеет место равенство:
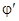 (x) = f (x, φ(x)).
(x) = f (x, φ(x)).
Часто встречается следующая задача: найти решение дифференциального уравнения
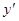 = f (x, y), (16.4)
= f (x, y), (16.4)
удовлетворяющее начальному условию:
y (x0) = y0. (16.5)
Предположим, что функция f (x,y) дифференцируема сколь угодно много раз в точке (x0,y0), а функция φ(x) является решением задачи (16.4)-(16.5). Тогда
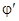 (x) = f(x, φ(x)),
(x) = f(x, φ(x)),
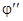 (x) =
(x) = 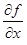 (x, φ(x)) +
(x, φ(x)) + 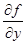 (x, φ(x))∙
(x, φ(x))∙ 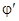 (x);
(x);
 (x) =
(x) = 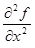 (x,φ(x)) +
(x,φ(x)) + 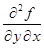 (x,φ(x))∙
(x,φ(x))∙ 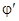 (x) +
(x) +
+  (x,φ(x))∙
(x,φ(x))∙ 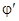 (x) +
(x) + 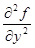 (x, φ(x))∙(
(x, φ(x))∙( 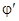 (x))2 +
(x))2 + 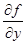 (x, φ(x))∙
(x, φ(x))∙ 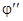 (x) ;
(x) ;
Аналогично, можно найти φ (4)(x), φ (5)(x), ... .
По условию, φ(x0) = y0. Тогда
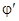 (x0) = f(x0, φ(x0)) = f(x0, y0);
(x0) = f(x0, φ(x0)) = f(x0, y0);
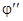 (x0) =
(x0) = 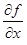 (x0, y0) +
(x0, y0) + 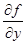 (x0, y0)∙
(x0, y0)∙ 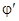 (x0);
(x0);
 (x0) =
(x0) = 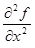 (x0, y0) +
(x0, y0) + 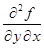 (x0, y0)∙
(x0, y0)∙ 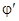 (x0) +
(x0) +  (x0,y0)∙
(x0,y0)∙ 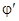 (x0) +
(x0) +
+ 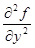 (x0, y0)∙(
(x0, y0)∙( 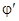 (x))2 +
(x))2 + 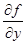 (x0, y0)∙
(x0, y0)∙ 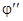 (x0) ,
(x0) ,
……..
Если степенной ряд
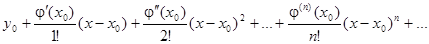
сходится в некоторой окрестности Sδ(x0), то функция
y = 
является приближенным решением задачи (16.4) - (16.5).
Пример. Найдем решение дифференциального уравнения
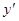 = y + x2,
= y + x2,
удовлетворяющее начальному условию:
y(0) = 1.
По условию, 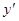 = y + x2. Тогда
= y + x2. Тогда
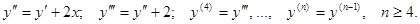
Значит, 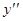 (0) =
(0) = 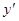 (0) = 1,
(0) = 1, 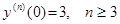 .
.
Степенной ряд
1 + 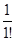 x +
x + 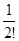 x2 +
x2 + 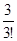 x3 +…+
x3 +…+ 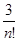 xn +…
xn +…
сходится на всей числовой прямой. Значит, искомое решение имеет вид:
y = 1 + x +  +
+ 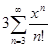 , где x
, где x  ]−∞, +∞[ .
]−∞, +∞[ .
Замечание.
Так как 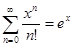 , x
, x  ]−∞, +∞[ , то
]−∞, +∞[ , то 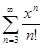 = ex – 1 − x −
= ex – 1 − x −  .
.
Тогда решение задачи можно записать в виде
y = 1 + x +  + 3(ex –1 − x −
+ 3(ex –1 − x −  ) = 3ex – 2 – 2x − x2.
) = 3ex – 2 – 2x − x2.
Тогда y(0) = 1; 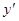 = 3ex – 2 – 2x; y + x2 = 3ex – 2 – 2x. Следовательно, функция y = 3ex – 2 – 2x − x2 действительно является решением данной задачи.
= 3ex – 2 – 2x; y + x2 = 3ex – 2 – 2x. Следовательно, функция y = 3ex – 2 – 2x − x2 действительно является решением данной задачи.
СПИСОК ЛИТЕРАТУРЫ
1. Барбаумов В. Е., Андреянов П. А., Смагина О. К.. N-мерное пространство. Функции. Экстремумы. М.: Изд-во Рос. экон. акад., 1992.
2. Барбаумов В. Е., Попова Н.В. Математический анализ.Интеграл Римана. М.: Изд-во Рос. экон. акад., 2007.
3. Демидович Б. П. Сборник задач и упражнений по математическому анализу. М.: АСТ ∙ Астрель, 2004.
4. Карташев А. П., Рождественский Б. Л. Математический анализ. М.: Наука, 1984.
5. Рождественский Б. Л. Лекции по математическому анализу. М.: Наука, 1972.
6. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. М.: ФИЗМАТЛИТ, 2003.
Дата добавления: 2016-07-09; просмотров: 7649;
