Основные свойства суммы степенных рядов
Теорема 13.1 (о непрерывности суммы степенного ряда). Если степенной ряд 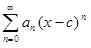 не является всюду расходящимся, то его сумма непрерывна в области сходимости этого ряда.
не является всюду расходящимся, то его сумма непрерывна в области сходимости этого ряда.
Доказательство. Все члены степенного ряда непрерывны на числовой прямой ]−∞, +∞[, а сам ряд сходится равномерно на любом отрезке в области его сходимости. По теореме о непрерывности суммы функционального ряда, сумма степенного ряда 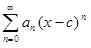 непрерывна на любом отрезке в области его сходимости. Это означает, что сумма степенного ряда непрерывна во всей области его сходимости.
непрерывна на любом отрезке в области его сходимости. Это означает, что сумма степенного ряда непрерывна во всей области его сходимости.
Пример.Дан степенной ряд  . Область сходимости данного ряда Ω = [−1,1]. Значит,
. Область сходимости данного ряда Ω = [−1,1]. Значит,
 = S(x), где x
= S(x), где x  [−1,1].
[−1,1].
По теореме 13.1 функция S(x) непрерывна на отрезке [−1,1].
Теорема 13.2 (о почленном интегрировании степенного ряда). Пусть степенной ряд 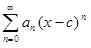 не является всюду расходящимся.
не является всюду расходящимся.
Если 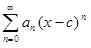 = S(x), x
= S(x), x  Ω, то
Ω, то
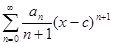 =
= 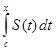 , x
, x  Ω.
Ω.
Доказательство. По теореме о почленном интегрировании функционального ряда, степенной ряд 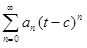 = S(t) можно интегрировать почленно на отрезке [c,x], где x
= S(t) можно интегрировать почленно на отрезке [c,x], где x  Ω. Тогда
Ω. Тогда  =
= 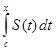 , x
, x  Ω. Отсюда получаем
Ω. Отсюда получаем
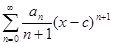 =
= 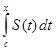 для любого x
для любого x  Ω.
Ω.
Пример. Степенной ряд 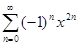 является геометрической прогрессией со знаменателем q = − x2. Следовательно, Ω = ]−1,1[. Тогда
является геометрической прогрессией со знаменателем q = − x2. Следовательно, Ω = ]−1,1[. Тогда 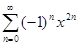 =
= 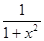 , где x
, где x  ]−1,1[. По теореме об интегрируемости суммы степенного ряда
]−1,1[. По теореме об интегрируемости суммы степенного ряда
 =
= 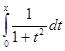 = arctg x, где x
= arctg x, где x  ]−1,1[ .
]−1,1[ .
Однако степенной ряд  сходится на отрезке [−1,1], а его сумма S(x) непрерывна на этом отрезке. Следовательно,
сходится на отрезке [−1,1], а его сумма S(x) непрерывна на этом отрезке. Следовательно,
 = arctg x, где x
= arctg x, где x  [−1,1].
[−1,1].
В частности, при x = 1 получим
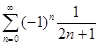 = arctg 1 =
= arctg 1 =  .
.
Если дан степенной ряд 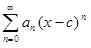 , то можно рассмотреть новый ряд
, то можно рассмотреть новый ряд 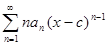 , полученный почленным дифференцированием исходного ряда.
, полученный почленным дифференцированием исходного ряда.
Лемма. При почленном дифференцировании степенного ряда 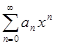 его радиус сходимости не изменяется.
его радиус сходимости не изменяется.
Доказательство. Предположим, что число R > 0 является радиусом сходимости ряда 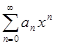 . Докажем, что ряд
. Докажем, что ряд 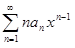 , полученный почленным дифференцированием исходного ряда, сходится на интервале ]−R,R[. Если x1
, полученный почленным дифференцированием исходного ряда, сходится на интервале ]−R,R[. Если x1  ]−R,R[, то |x1| < R. Тогда найдётся число zтакое, что |x1| < z < R. Так как число z принадлежит интервалу сходимости ряда
]−R,R[, то |x1| < R. Тогда найдётся число zтакое, что |x1| < z < R. Так как число z принадлежит интервалу сходимости ряда 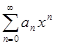 , то числовой ряд
, то числовой ряд 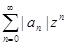 сходится. По необходимому признаку сходимости
сходится. По необходимому признаку сходимости 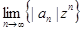 = 0. Следовательно, существует число М > 0 такое, что
= 0. Следовательно, существует число М > 0 такое, что  ≤ М для любого n
≤ М для любого n  N. Тогда
N. Тогда
 =
=  .
.
Числовой ряд 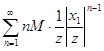 сходится, так как для этого ряда
сходится, так как для этого ряда
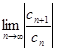 =
= 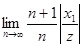 =
= 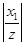 < 1.
< 1.
Тогда сходится ряд 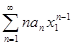 .
.
Таким образом, мы доказали, что ряд 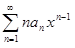 сходится на интервале ]−R,R[. Следовательно, при почленном дифференцировании радиус сходимости не уменьшается. Покажем, что при почленном дифференцировании радиус сходимости не может и увеличиваться.
сходится на интервале ]−R,R[. Следовательно, при почленном дифференцировании радиус сходимости не уменьшается. Покажем, что при почленном дифференцировании радиус сходимости не может и увеличиваться.
Предположим, что степенной ряд 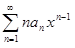 сходится на интервале ]−R1,R1[, где R1 > R. Степенной ряд
сходится на интервале ]−R1,R1[, где R1 > R. Степенной ряд 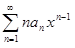 можно почленно интегрировать на отрезке [0, z], где |z| < R1. Тогда ряд
можно почленно интегрировать на отрезке [0, z], где |z| < R1. Тогда ряд 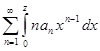 =
= 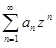 будет сходящимся. Следовательно, степенной ряд
будет сходящимся. Следовательно, степенной ряд 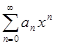 сходится при любом x
сходится при любом x  ]−R1, R1[. Однако по условию радиус сходимости этого ряда равен R, причем R < R1. Противоречие.
]−R1, R1[. Однако по условию радиус сходимости этого ряда равен R, причем R < R1. Противоречие.
Следствие. При почленном дифференцировании степенного ряда 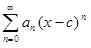 его радиус сходимости не изменяется.
его радиус сходимости не изменяется.
Теорема 13.3. Если степенной ряд 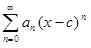 не является всюду расходящимся, то его можно почленно дифференцировать сколь угодно много раз внутри интервала сходимости. Если
не является всюду расходящимся, то его можно почленно дифференцировать сколь угодно много раз внутри интервала сходимости. Если
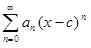 = S(x), x
= S(x), x  ] c − R , c + R [,
] c − R , c + R [,
то
 =
=  (x), x
(x), x  ] c − R , c + R [,
] c − R , c + R [,
 =
= 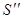 (x), x
(x), x  ] c − R , c + R [,
] c − R , c + R [,
…………………………….
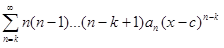 = S (k)(x), x
= S (k)(x), x  ] c − R , c + R [,
] c − R , c + R [,
……………………………….
Доказательство. Все члены ряда 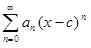 непрерывно дифференцируемы на числовой прямой, а сам ряд сходится на интервале ]c−R, c+R[. Ряд из производных
непрерывно дифференцируемы на числовой прямой, а сам ряд сходится на интервале ]c−R, c+R[. Ряд из производных  сходится равномерно на любом отрезке внутри этого интервала. По теореме 10.3 (о почленном дифференцировании функционального ряда), функция S(x) непрерывно дифференцируема на интервале ]c−R, c+R[. При этом
сходится равномерно на любом отрезке внутри этого интервала. По теореме 10.3 (о почленном дифференцировании функционального ряда), функция S(x) непрерывно дифференцируема на интервале ]c−R, c+R[. При этом
 =
=  (x), x
(x), x  ]c−R,c+R[.
]c−R,c+R[.
Повторяя эти рассуждения, получим, что функция  (x) непрерывно дифференцируема на интервале ]c−R, c+R[ , причем
(x) непрерывно дифференцируема на интервале ]c−R, c+R[ , причем
 =
= 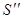 (x), x
(x), x  ] c − R , c + R [.
] c − R , c + R [.
И так далее.
Пример.Рассмотрим степенной ряд 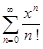 . Этот ряд сходится на всей числовой прямой. Тогда
. Этот ряд сходится на всей числовой прямой. Тогда
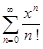 = S(x), где x
= S(x), где x  ]−∞, +∞[.
]−∞, +∞[.
По теореме 13.3,
 =
=  (x), где x
(x), где x  ]−∞, +∞[.
]−∞, +∞[.
Так как ряды 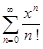 и
и  совпадают, то
совпадают, то
S(x) =  (x), x
(x), x  ]−∞, +∞[.
]−∞, +∞[.
Положим f(x) = S(x)e−x. Тогда
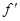 (x) =
(x) =  (x)e−x − S(x)e−x = e−x (
(x)e−x − S(x)e−x = e−x (  (x) − S(x)) = 0, где x
(x) − S(x)) = 0, где x  ]−∞, +∞[.
]−∞, +∞[.
Следовательно, f(x) = c, x  ]−∞,+∞[ и S(x) = cex.
]−∞,+∞[ и S(x) = cex.
Очевидно, что S(0) = 1. Тогда c = 1. Таким образом, S(x) = ex и
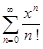 = ex, x
= ex, x  ]−∞, +∞[.
]−∞, +∞[.
Задачи.
13.1. Исследовать функцию S(x) на непрерывность:
а) S(x) =  ; б) S(x) =
; б) S(x) =  ;
;
в) S(x) = 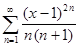 ; г) S(x) =
; г) S(x) = 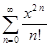 ;
;
13.2. Найти сумму степенного ряда:
а)  ; б)
; б) 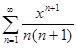 .
.
Указание. Воспользоваться равенством
 =
= 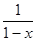 , x
, x  ]−1, 1[.
]−1, 1[.
13.3. Найти сумму степенного ряда:
а)  ; б)
; б) 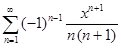 .
.
13.4. С помощью почленного дифференцирования степенного ряда найти его сумму:
а) 1 + 2x + 3x2 + … + nxn−1 + … ;
б) 1 − 2x + 3x2 − 4x3 + … + (−1)n−1 (n + 1)xn + …;
в) 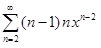 ;
;
г) 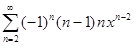 .
.
Ряды Тейлора
Если функция f(x) n раз дифференцируема в точке x0  R, то имеет место формула Тейлора:
R, то имеет место формула Тейлора:
f(x) = f(x0) + 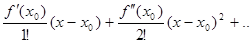
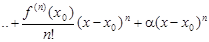 ,
,
где α → 0 при x → x0.
Если же функция f(x) дифференцируема в точке x0 сколь угодно много раз, то можно составить ряд Тейлора для функции f(x):
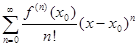 .
.
Замечание. Если x0 = 0, то степенной ряд
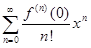
называется рядом Маклорена для функции f(x).
Примеры.1. Рассмотрим функцию f(x) = sin x. Тогда
f (n)(x) = 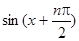 , n = 0,1,2, ...
, n = 0,1,2, ...
Следовательно, если n − чётное число, то f (n)(0) = 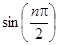 = 0.
= 0.
Если n = 2k – 1, k = 1,2,3, ..., то f (n)(0) =  = (−1)k−1.
= (−1)k−1.
Тогда ряд Маклорена для функции f(x) = sinx имеет вид:
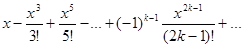
2. Если f(x) = cos x, то f (n)(x) =  , n = 1,2,3, .. .
, n = 1,2,3, .. .
Если n – нечётное число, то f (n)(0) = 0 и f (n)(0) = (−1)k, если
n = 2k, k = 0,1,2,3, ... . Тогда ряд Маклорена для функции
f(x) = cosx имеет вид:
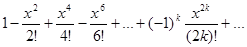
Дата добавления: 2016-07-09; просмотров: 3896;
