Степенные ряды. Область сходимости степенного ряда
Функциональный ряд вида
а0 + а1 (x − c) + а2 (x − c)2 + …+ аn (x − c)n + …
называется степенным рядом. Числа
а0, а1, а2, …, аn , …
называются коэффициентами степенного ряда, а число c – центром степенного ряда.
Степенной ряд с центром в точке c можно записать кратко:
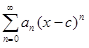 .
.
Если c = 0, то степенной ряд с центром в нуле имеет вид:
а0 + а1 x + а2 x2 + …+ аn xn + …, или 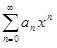 .
.
Очевидно, что степенной ряд 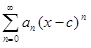 всегда сходится при x = c. Если степенной ряд
всегда сходится при x = c. Если степенной ряд 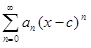 сходится только при x = c, то он называется всюду расходящимся. Если же степенной ряд сходится на всей числовой прямой, то его называют всюду сходящимся.
сходится только при x = c, то он называется всюду расходящимся. Если же степенной ряд сходится на всей числовой прямой, то его называют всюду сходящимся.
Теорема 11.1(теорема Абеля). Если степенной ряд 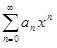 сходится при x = x 1 ≠ 0, то он сходится и притом абсолютно при всех│x│<│x1│.Если степенной ряд
сходится при x = x 1 ≠ 0, то он сходится и притом абсолютно при всех│x│<│x1│.Если степенной ряд 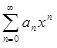 расходится при x = x2, то он расходится при всех │x│>│x 2│.
расходится при x = x2, то он расходится при всех │x│>│x 2│.
Доказательство. Предположим, что степенной ряд 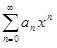 сходится при x = x1 ≠ 0. Это означает, что сходится числовой ряд
сходится при x = x1 ≠ 0. Это означает, что сходится числовой ряд 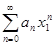 . В силу необходимого признака сходимости числового ряда
. В силу необходимого признака сходимости числового ряда 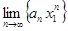 = 0. Значит, существует число М > 0 такое, что
= 0. Значит, существует число М > 0 такое, что
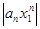 ≤ M, n
≤ M, n  N.
N.
Если│x│<│x1│,то
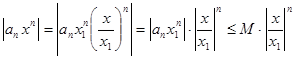 , n
, n  N.
N.
Ряд 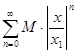 сходится, так как является геометрической прогрессией со знаменателем q =
сходится, так как является геометрической прогрессией со знаменателем q = 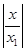 < 1. Тогда ряд
< 1. Тогда ряд 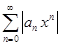 сходится при всех│x│<│x1│, так как имеет сходящуюся мажоранту
сходится при всех│x│<│x1│, так как имеет сходящуюся мажоранту 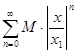 . Следовательно, степенной ряд
. Следовательно, степенной ряд 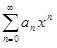 сходится абсолютно при всех │x│<│x1│.
сходится абсолютно при всех │x│<│x1│.
Предположим, что степенной ряд 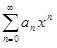 расходится при x = x2, но сходится при x = x3, где │x3│>│x2│(см. рис. 11.1). Из уже доказанного следует, что степенной ряд
расходится при x = x2, но сходится при x = x3, где │x3│>│x2│(см. рис. 11.1). Из уже доказанного следует, что степенной ряд 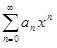 должен сходиться на интервале ]−│x3│,│x3│[, что противоречит условию, поскольку
должен сходиться на интервале ]−│x3│,│x3│[, что противоречит условию, поскольку
x2  ]−│x3│, │x3│[.
]−│x3│, │x3│[. 

сходимость
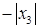
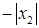 0
0 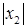
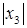
Рис. 11.1.
Следствие 1. Если степенной ряд 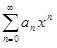 не является всюду сходящимся или всюду расходящимся, то существует число R > 0 такое, что степенной ряд сходится абсолютно при всех│x│< R и расходится при всех│x│> R .
не является всюду сходящимся или всюду расходящимся, то существует число R > 0 такое, что степенной ряд сходится абсолютно при всех│x│< R и расходится при всех│x│> R .
Доказательство. По условию существуют точки: x1 ≠ 0, в которой ряд сходится и x2, в которой ряд расходится. Если Ω − область сходимости степенного ряда 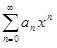 , то по теореме Абеля имеем ]−│x1│, │x1│[
, то по теореме Абеля имеем ]−│x1│, │x1│[ 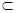 Ω и Ω
Ω и Ω 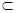 ] −│x2│, │x2│[ (см. рис. 11.2).
] −│x2│, │x2│[ (см. рис. 11.2).

расходимость сходимость расходимость
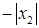
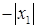 0
0 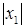
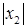
Рис.11.2.
Так как числовое множество Ω ограничено сверху, то существует число R = Sup Ω. Очевидно, что R > 0.
Покажем, что степенной ряд 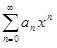 расходится при всех │x│> R и сходится абсолютно при всех│x│< R .
расходится при всех │x│> R и сходится абсолютно при всех│x│< R .
Если степенной ряд 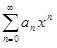 сходится при x = y, где │y│> R, то по теореме Абеля ]−│y│, │y│[
сходится при x = y, где │y│> R, то по теореме Абеля ]−│y│, │y│[ 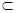 Ω. Тогда Sup Ω ≥ │y│> R. Противоречие. Следовательно, степенной ряд расходится при всех│x│> R.
Ω. Тогда Sup Ω ≥ │y│> R. Противоречие. Следовательно, степенной ряд расходится при всех│x│> R.
Если же ряд 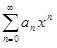 расходится при x = z, где│z│< R, то
расходится при x = z, где│z│< R, то
Ω 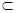 ] −│z│, │z│[ . Тогда R = Sup Ω ≤ │z│< R. Из полученного противоречия (R < R) следует, что степенной ряд
] −│z│, │z│[ . Тогда R = Sup Ω ≤ │z│< R. Из полученного противоречия (R < R) следует, что степенной ряд 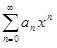 сходится при всех│x│< R, причем абсолютно.
сходится при всех│x│< R, причем абсолютно.
Следствие 2. Если степенной ряд 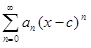 не является всюду сходящимся или всюду расходящимся, то существует число
не является всюду сходящимся или всюду расходящимся, то существует число
R > 0 такое, что степенной ряд 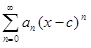 сходится абсолютно при всех│x − c │< R и расходится при всех│x − c │> R.
сходится абсолютно при всех│x − c │< R и расходится при всех│x − c │> R.
Доказательство. Положим z = x − c. Тогда степенной ряд примет вид: 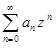 . По первому следствию, найдется число R > 0 такое, что степенной ряд
. По первому следствию, найдется число R > 0 такое, что степенной ряд 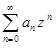 сходится абсолютно при всех│z│< R и расходится при всех │z│> R. Следовательно, степенной ряд
сходится абсолютно при всех│z│< R и расходится при всех │z│> R. Следовательно, степенной ряд 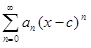 сходится абсолютно при │x − c │< R и расходится при │x − c │> R.
сходится абсолютно при │x − c │< R и расходится при │x − c │> R.
Определение.Число R > 0 такое, что ряд 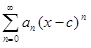 сходится абсолютно при│x − c│< R и расходится при│x − c│> R, называется радиусом сходимости этого ряда.
сходится абсолютно при│x − c│< R и расходится при│x − c│> R, называется радиусом сходимости этого ряда.
Интервал ]c − R, c + R[ называется интервалом сходимости степенного ряда 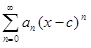 .
.
Замечание. Будем считать, что радиус сходимости всюду сходящегося ряда равен + ∞, а всюду расходящегося 0.
Чтобы найти область сходимости Ω степенного ряда 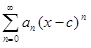 , необходимо вначале определить радиус сходимости этого ряда R. Если R = 0, то область сходимости ряда Ω = {c}.
, необходимо вначале определить радиус сходимости этого ряда R. Если R = 0, то область сходимости ряда Ω = {c}.
Если R = +∞, то Ω = ]− ∞, + ∞[ . Если же 0 < R < + ∞, то интервал сходимости ряда ]c−R,c+R[ 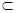 Ω и степенной ряд
Ω и степенной ряд 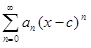 расходится при всех│x − c│> R. Для отыскания области сходимости Ω степенного ряда достаточно выяснить сходится или расходится ряд
расходится при всех│x − c│> R. Для отыскания области сходимости Ω степенного ряда достаточно выяснить сходится или расходится ряд 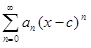 при x = c − R и x = c + R.
при x = c − R и x = c + R.
Примеры. 1.Рассмотрим степенной ряд 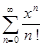 . Для отыскания радиуса сходимости этого ряда воспользуемся признаком Даламбера:
. Для отыскания радиуса сходимости этого ряда воспользуемся признаком Даламбера:
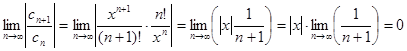 .
.
Так как 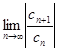 = 0 < 1 при любом x
= 0 < 1 при любом x 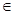 ]− ∞, + ∞[, то степенной ряд сходится абсолютно на всей числовой прямой. Следовательно, R = +∞, Ω = ]− ∞, + ∞[ .
]− ∞, + ∞[, то степенной ряд сходится абсолютно на всей числовой прямой. Следовательно, R = +∞, Ω = ]− ∞, + ∞[ .
2. Дан степенной ряд 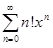 . Очевидно, что x = 0
. Очевидно, что x = 0 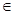 Ω.
Ω.
При x ≠ 0 получим

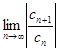 =
= 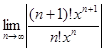 = | x |
= | x | 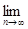 (n + 1) = ∞.
(n + 1) = ∞.
Тогда по признаку Даламбера степенной ряд 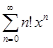 расходится при всех x ≠ 0. Ряд является всюду расходящимся, его радиус сходимости R = 0, область сходимости Ω = {0}.
расходится при всех x ≠ 0. Ряд является всюду расходящимся, его радиус сходимости R = 0, область сходимости Ω = {0}.
3. Дан степенной ряд 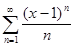 . Рассмотрим
. Рассмотрим

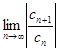 =
= 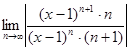 = |x −1|∙
= |x −1|∙ 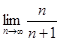 = |x − 1|.
= |x − 1|.
Тогда по признаку Даламбера степенной ряд сходится абсолютно, если │x −1│< 1 и расходится при │x − 1│> 1. Следовательно, радиус сходимости ряда R = 1, а интервал сходимости ]0, 2[ . Если x = 2, то мы получим расходящийся числовой ряд 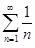 , а при x = 0 ряд имеет вид:
, а при x = 0 ряд имеет вид: 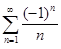 . Этот числовой ряд сходится условно в силу теоремы Лейбница. Следовательно, область сходимости степенного ряда − полуинтервал Ω = [0, 2[.
. Этот числовой ряд сходится условно в силу теоремы Лейбница. Следовательно, область сходимости степенного ряда − полуинтервал Ω = [0, 2[.
Задачи.
11.1. Найти область сходимости степенного ряда:
а) 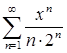 ; б)
; б) 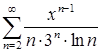 ;
;
в) 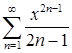 ; г)
; г) 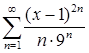 ;
;
д) 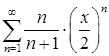 ; е)
; е) 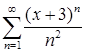 ;
;
ж) 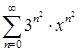 ; з)
; з) 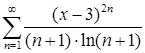 .
.
11.2. Найти область сходимости степенного ряда:
а) 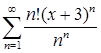 ; б)
; б) 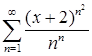 ;
;
в) 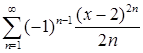 ; г)
; г) 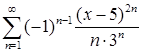 ;
;
д) 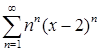 ; е)
; е) 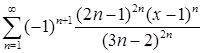 .
.

Дата добавления: 2016-07-09; просмотров: 1479;
