Простейшие утверждения о равномерной сходимости функциональных рядов.
1. Функциональный ряд 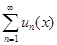 сходится к функции S(x) равномерно на множестве W тогда и только тогда, когда для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N одновременно для всех x
сходится к функции S(x) равномерно на множестве W тогда и только тогда, когда для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N одновременно для всех x  W выполняется неравенство
W выполняется неравенство
|Sn(x) − S(x)| < ε .
2. Функциональный ряд 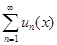 сходится на множестве W равномерно тогда и только тогда, когда для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N одновременно для всех x
сходится на множестве W равномерно тогда и только тогда, когда для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N одновременно для всех x  W выполняется неравенство
W выполняется неравенство
|Sn(x) – Sm(x)| < ε.
3. Если функциональные ряды 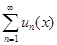 и
и 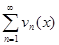 сходятся на множестве W равномерно, а λ и μ – некоторые числа, то и ряд
сходятся на множестве W равномерно, а λ и μ – некоторые числа, то и ряд 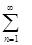 (λun(x)+μvn(x)) сходится на этом множестве равномерно.
(λun(x)+μvn(x)) сходится на этом множестве равномерно.
4. Если функциональный ряд 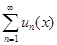 сходится на множестве W равномерно, а функция φ(x) ограничена на этом множестве, то и ряд
сходится на множестве W равномерно, а функция φ(x) ограничена на этом множестве, то и ряд 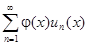 сходится на множестве W равномерно.
сходится на множестве W равномерно.
Теорема 9.1 (признак равномерной сходимости Вейерштрасса). Функциональный ряд 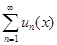 сходится на множестве W равномерно и абсолютно, если │un(x)│≤ an для всех x
сходится на множестве W равномерно и абсолютно, если │un(x)│≤ an для всех x  W и n
W и n  N, а числовой ряд
N, а числовой ряд 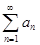 сходится.
сходится.
Доказательство. Если числовой ряд 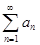 сходится, то сходится и последовательность его частичных сумм {Sn}. Значит, последовательность {Sn} является фундаментальной. Тогда, для любого ε > 0 существует номер N = N(ε) такой, что при всех
сходится, то сходится и последовательность его частичных сумм {Sn}. Значит, последовательность {Sn} является фундаментальной. Тогда, для любого ε > 0 существует номер N = N(ε) такой, что при всех
m, n ≥ N выполняется неравенство 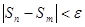 .
.
Рассмотрим последовательность частичных сумм функционального ряда 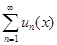 . Если m > n ≥ N, то
. Если m > n ≥ N, то
|Sm(x) − Sn(x)| = |u1(x)+...+ un(x)+ un+1(x)+...+ um(x) − u1(x) −...− un(x)| =
= |un+1(x) + un+2(x) +...+ um(x)| ≤ | un+1(x)| + | un+2(x)| +...+ | um(x)| ≤
≤ an+1 + an+2 +...+ am = Sm − Sn = |Sm − Sn| < ε.
Аналогично, если n > m ≥ N , то
|Sn(x) − Sm(x)| ≤ Sn − Sm = | Sn − Sm | < ε.
Таким образом, для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N одновременно для всех x  W выполняется неравенство |Sn(x) – Sm(x)| < ε.
W выполняется неравенство |Sn(x) – Sm(x)| < ε.
По утверждению 2 функциональный ряд 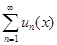 сходится на множестве W равномерно. Теорема доказана.
сходится на множестве W равномерно. Теорема доказана.
Примеры.1. Функциональный ряд 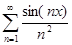 сходится равномерно и абсолютно на всей числовой прямой, так как
сходится равномерно и абсолютно на всей числовой прямой, так как 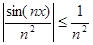 для всех x
для всех x  ]−∞, +∞[ и n
]−∞, +∞[ и n  N, а числовой ряд
N, а числовой ряд 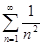 сходится.
сходится.
2. Покажем, что функциональный ряд 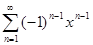 сходится равномерно на любом отрезке [a, b]
сходится равномерно на любом отрезке [a, b] 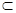 ]−1,+1[. Положим
]−1,+1[. Положим
c = max{|a|,|b|}.
Тогда для всех x  [a,b] выполняется неравенство│x│≤ c. Значит, если x
[a,b] выполняется неравенство│x│≤ c. Значит, если x  [a,b], то
[a,b], то
|(−1)n−1 xn−1| = |x|n−1 ≤ cn−1, n  N .
N .
Числовой ряд 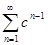 является сходящимся, так как 0 < c < 1. Тогда по признаку равномерной сходимости Вейерштрасса, ряд
является сходящимся, так как 0 < c < 1. Тогда по признаку равномерной сходимости Вейерштрасса, ряд 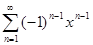 сходится равномерно и абсолютно на отрезке [a,b]
сходится равномерно и абсолютно на отрезке [a,b]  ]−1,+1[.
]−1,+1[.
Задачи.
9.1. Найти область сходимости функционального ряда:
а) 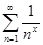 ; б)
; б) 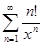 ; в)
; в) 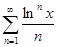 ; г)
; г) 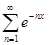 ;
;
д) 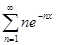 ; е)
; е) 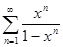 ; ж)
; ж) 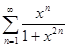 ;
;
з) 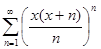 ; и)
; и) 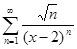 ; к)
; к) 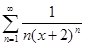 .
.
9.2. Найти область сходимости функционального ряда:
а) 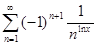 ; б)
; б) 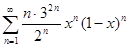 ; в)
; в) 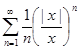 ;
;
г) 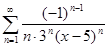 ; д)
; д) 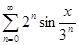 ; е)
; е) 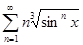 .
.
9.3. На указанном множестве исследовать равномерную сходимость функционального ряда:
а) 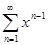 ; | x | ≤ q <1;
; | x | ≤ q <1;
б) 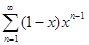 ; x
; x  [0, 1];
[0, 1];
в) 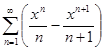 ; x
; x  [−1, 1];
[−1, 1];
г) 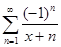 ; x
; x  [0, + ∞[ ;
[0, + ∞[ ;
д) 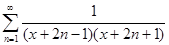 ; x
; x  [0, + ∞[ ;
[0, + ∞[ ;
е) 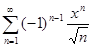 ; x
; x  [0, 1];
[0, 1];
ж) 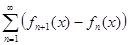 , где fn(x) =
, где fn(x) = 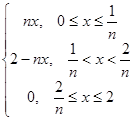 .
.
9.4. Исследовать равномерную сходимость функционального ряда, используя признак Вейерштрасса:
а) 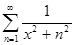 ; x
; x  ]− ∞, + ∞[;
]− ∞, + ∞[;
б) 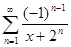 ; x
; x  ]− 2, + ∞[;
]− 2, + ∞[;
в) 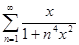 ; x
; x  [ 0, + ∞[;
[ 0, + ∞[;
г) 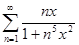 ; x
; x  ]− ∞, + ∞[;
]− ∞, + ∞[;
д) 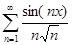 ; x
; x  ]− ∞, + ∞[;
]− ∞, + ∞[;
е) 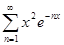 ; x
; x  [0, + ∞[;
[0, + ∞[;
ж) 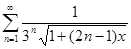 ; x
; x  [ 0, + ∞[.
[ 0, + ∞[.
Дата добавления: 2016-07-09; просмотров: 955;
