Простейшие утверждения о равномерной сходимости
1. Если {fn(x)} 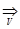 f(x), а множество W
f(x), а множество W 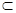 V, то {fn(x)}
V, то {fn(x)} 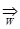 f(x).
f(x).
2. Если {fn(x)} 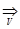 f(x) и {φn(x)}
f(x) и {φn(x)} 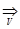 φ(x), а λ и μ− некоторые числа, то последовательность
φ(x), а λ и μ− некоторые числа, то последовательность
{λ fn(x) + μ φn(x)} 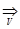 λ f(x) + μφ(x).
λ f(x) + μφ(x).
3. Если последовательность {fn(x)} 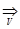 f(x), а функция φ(x) ограничена на множестве V, то {φ(x) fn(x)}
f(x), а функция φ(x) ограничена на множестве V, то {φ(x) fn(x)} 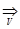 φ(x) f(x).
φ(x) f(x).
4. Если {fn(x)} 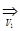 f(x), {fn(x)}
f(x), {fn(x)} 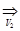 f(x), то {fn(x)}
f(x), то {fn(x)} 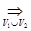 f(x).
f(x).
5. Пусть для каждого n  Nсуществует число
Nсуществует число
dn = 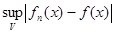 .
.
Последовательность {fn(x)} сходится к функции f(x) равномерно на множестве V тогда и только тогда, когда 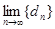 = 0.
= 0.
Доказательство необходимости.Если {fn(x)} 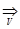 f(x), то для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N и x
f(x), то для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N и x  V выполняется неравенство │fn(x) − f(x)│<
V выполняется неравенство │fn(x) − f(x)│< 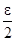 . Тогда
. Тогда
dn = 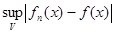 ≤
≤ 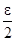 < ε.
< ε.
Таким образом, для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N выполняется неравенство dn < ε. Значит, 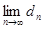 = 0.
= 0.
Доказательство достаточности.Если 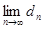 = 0, то для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N выполняется неравенство dn =
= 0, то для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N выполняется неравенство dn = 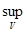 │fn(x) − f(x)│< ε. Это означает, что при всех n ≥ N одновременно для всех x
│fn(x) − f(x)│< ε. Это означает, что при всех n ≥ N одновременно для всех x  V выполняется неравенство │fn(x) − f(x)│< ε. Значит, {fn(x)}
V выполняется неравенство │fn(x) − f(x)│< ε. Значит, {fn(x)} 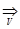 f(x).
f(x).
Пример.Рассмотрим функциональную последовательность {xn – x2 n}, где 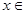 [0,1]. Очевидно, что {xn – x2n}
[0,1]. Очевидно, что {xn – x2n} 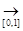 φ(x) = 0. Выясним, является ли эта сходимость равномерной. Функция φn(x) = xn – x2n непрерывна на отрезке [0,1] и, следовательно, достигает на этом отрезке своей точной верхней грани. Найдем
φ(x) = 0. Выясним, является ли эта сходимость равномерной. Функция φn(x) = xn – x2n непрерывна на отрезке [0,1] и, следовательно, достигает на этом отрезке своей точной верхней грани. Найдем
dn = 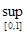 |φn(x) – 0| =
|φn(x) – 0| = 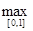 (φn(x)).
(φn(x)).
Поскольку
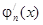 = nxn – 1 – 2nx2n – 1 = nxn – 1(1 – 2xn ),
= nxn – 1 – 2nx2n – 1 = nxn – 1(1 – 2xn ),
то 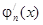 = 0
= 0 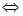 x1 = 0 или x2 =
x1 = 0 или x2 = 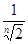 . Так какφn(0) = 0, φn(1) = 0,
. Так какφn(0) = 0, φn(1) = 0, 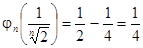 , то dn =
, то dn = 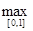 (φn(x)) =
(φn(x)) = 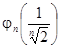 =
= 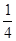 . Поскольку
. Поскольку 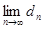 =
= 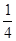 ≠ 0, то сходимость {φn(x)}
≠ 0, то сходимость {φn(x)} 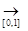 φ (x) = 0 не является равномерной.
φ (x) = 0 не является равномерной.
Задачи.
7.1. Найти 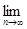 {fn(x)}, если:
{fn(x)}, если:
а) fn(x) = 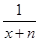 ,
, 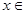 [0, +∞[ ; б) fn(x) = 1 – x2 n ,
[0, +∞[ ; б) fn(x) = 1 – x2 n , 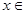 [–1, 1];
[–1, 1];
в) fn(x) = 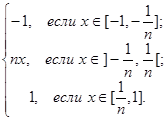
г) fn(x) = 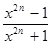 , x
, x  ] − ∞ , + ∞[ ;
] − ∞ , + ∞[ ;
д) fn(x) = 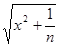 , x
, x  ] − ∞ , + ∞[;
] − ∞ , + ∞[;
е) fn(x) = 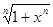 , x
, x  ]0 , + ∞[ ;
]0 , + ∞[ ;
ж) fn(x) = 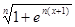 , x
, x  ]− ∞ , + ∞[ .
]− ∞ , + ∞[ .
7.2. Исследовать функциональную последовательность на равномерную сходимость:
а) {x2n}, x  [0 ,
[0 , 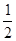 ] ; б) {x2n}, x
] ; б) {x2n}, x  [0 , 1];
[0 , 1];
в) 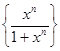 , x
, x  [0 ,
[0 , 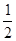 ]; г)
]; г) 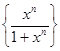 , x
, x  [–
[– 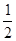 ,
, 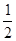 ];
];
д) 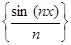 , x
, x  ]− ∞ , + ∞[; е)
]− ∞ , + ∞[; е) 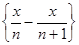 , x
, x  [0 , 1];
[0 , 1];
ж) 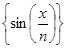 , x
, x  ]−∞,+∞[; з)
]−∞,+∞[; з) 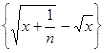 , x
, x  [0,+ ∞[;
[0,+ ∞[;
7.3. Исследовать функциональную последовательность на равномерную сходимость:
а) {xn – xn+1}, x  [0 , 1]; б) {arctg nx}, x
[0 , 1]; б) {arctg nx}, x  [0 ,+ ∞[;
[0 ,+ ∞[;
в) 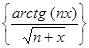 , x
, x  [0 , + ∞[; г)
[0 , + ∞[; г) 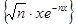 , x
, x  [0 ,+ ∞[;
[0 ,+ ∞[;
д) 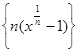 , x
, x  [1, 10];
[1, 10];
е) { fn(x)}, где fn(x) = 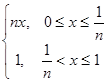 .
.
7.4. Доказать, что {fn(x)} 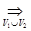 f(x),если {fn(x)}
f(x),если {fn(x)} 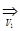 f(x) и {fn(x)
f(x) и {fn(x) 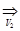 f(x).
f(x).
7.5. Доказать, что {λ fn(x) + μφn(x)} 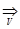 λ f(x) + μφ(x), если
λ f(x) + μφ(x), если
{fn(x)} 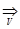 f(x) и
f(x) и 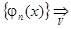 φ(x).
φ(x).
7.6. Доказать, что 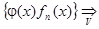 φ(x)∙f(x), если {fn(x)}
φ(x)∙f(x), если {fn(x)} 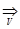 f(x), а функция φ(x) ограничена на множестве V.
f(x), а функция φ(x) ограничена на множестве V.
7.7. Доказать, что функциональная последовательность {fn(x)} сходится на множестве V, если:
а) fn(x) = x + 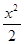 +…+
+…+ 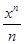 , n
, n  N; V = ]−1, 1[;
N; V = ]−1, 1[;
б) fn(x) = x – 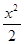 +
+ 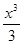 –
– 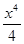 …+(–1)n−1
…+(–1)n−1 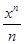 , n
, n  N; V = ]−1, 1[;
N; V = ]−1, 1[;
в) fn(x) = x + 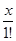 +
+ 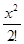 +…+
+…+ 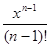 , n
, n  N; V = ]−1, 1[.
N; V = ]−1, 1[.
Дата добавления: 2016-07-09; просмотров: 1011;
