Сходимость и равномерная сходимость функциональных последовательностей

Пусть V 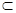R − некоторое числовое множество. Говорят, что на множестве V задана функциональная последовательность 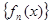, если каждому натуральному числу n поставлена в соответствие функция f_n(x), определенная на множестве V.

Замечание.Если на множестве V задана функциональная последовательность 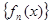, то при каждом фиксированном 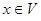определена числовая последовательность 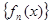. Например, функциональная последовательность 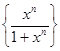определена на полуинтервале [0,+∞[. Тогда при x = 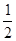имеем числовую последовательность 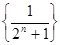. Если же x = 2, то числовая последовательность имеет вид .

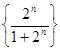Определение 1.Говорят, чтофункциональная последовательность 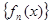сходится на множестве V к функции f(x), если в каждой точке 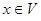числовая последовательность 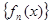сходится к значению функции f(x) в точке x, т.е. к числу f(x).

Функцию f(x) называют пределом последовательности 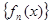и пишут 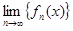= f(x). Запись вида 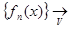f(x) означает, что функциональная последовательность 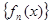сходится к функции f(x) на множестве V .

Примеры.1.Рассмотрим последовательность 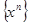на отрезке [0,1]. Если 0 ≤ x < 1, то 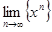= 0. Если x = 1, то 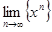= 1. Следовательно, 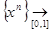f(x), где

f(x) = .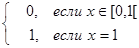

Графики функций y = xⁿ для n = 1,2,3,4,5 и функции f(x), где 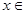[0,1], приведены на рисунке 7.1.

Рис. 7.1.

2. Последовательность 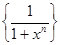определена на полуинтервале [0, +∞[. Если 0 ≤ x < 1, то xⁿ → 0 и 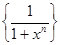→ 1. Если x = 1, то 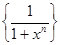→ 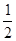. Если x > 1, то xⁿ → + ∞ и 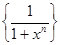→ 0. Таким образом,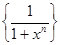 f (x), где

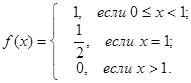
Графики функций y = 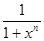для n = 1,2,3 и функции f(x), где 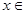[0, +∞[ , приведены на рисунке 7.2.

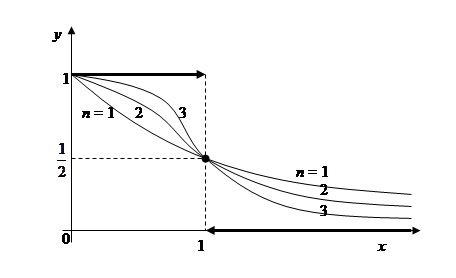
Рис. 7.2.

Из определения предела числовой последовательности следует, что 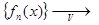f(x) тогда и только тогда, когда для каждого x V и любого ε > 0 существует номер N = N(ε, x) такой, что при всех n ≥ N выполняется неравенство │ f_n(x) − f(x)│< ε.

Важную роль играет понятие равномерной сходимости функциональной последовательности.

Определение 2.Говорят, чтоФункциональная последовательность 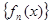сходится к функции f(x) на множестве V равномерно, если для любого ε > 0 существует номер N = N(ε) (зависящий только от ε) такой, что при всех n ≥ N одновременно для всех x V выполняется неравенство

│f_n(x) − f(x) │< ε.

Запись 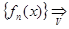f(x) означает, что последовательность 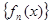сходится к функции f(x) на множестве V равномерно.

Пример.Рассмотрим последовательность 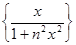, где

x ] − ∞ , + ∞[. Несложно убедиться, что эта последовательность сходится к функции f(x) = 0 на всей числовой прямой.

Для исследования на равномерную сходимость заметим, что

(1− n│x│)² ≥ 0. Отсюда 1 − 2 n│x│+ n²│x│² ≥ 0. Тогда

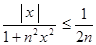, x ] − ∞ , + ∞[ , n N.

Так как 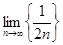= 0, то для любого ε > 0 существует N = N(ε) такой, что при всех n ≥ N выполняется неравенство 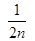< ε. Тогда при всех n ≥ N одновременно для всех x ]−∞,+ ∞[ получим

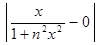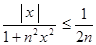= < ε.

Значит, сходимость последовательности к функции f(x) = 0 на всей числовой прямой является равномерной, то есть

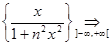f(x) = 0.

Геометрический смысл равномерной сходимости. Предположим, что функция f(x) определена на отрезке [a, b]. Для любого ε> 0 можно рассмотреть множество (см. рис. 7.3):

Q_ε ( f )= {M(x, y) R ²│ a ≤ x ≤ b, f(x) − ε < y < f(x) + ε }.

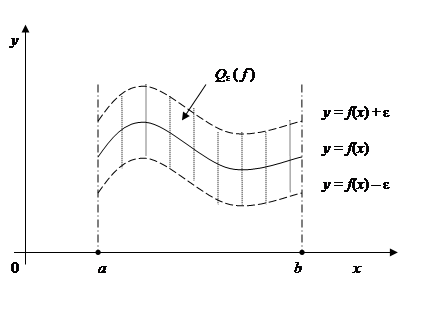
Рис. 7.3

Последовательность 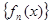сходится к функции f(x) на отрезке [a, b] равномерно тогда и только тогда, когда для любого ε > 0 существует номер N = N(ε) такой, что при n ≥ N график функции y = f_n(x) целиком находится в множестве Q_ε ( f ).

Пример.Рассмотрим последовательность 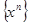на полуинтервале [0,1[.Из примера 1 следует, что 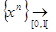f(x) = 0. Покажем, что эта сходимость не является равномерной. Предположим противное. Пусть 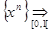f(x) = 0. Тогда для ε = 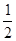найдется номер N такой, что при всех n ≥ N одновременно для всех x [0,1[ выполняется неравенство │ xⁿ − 0 │< 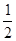. Отсюда xⁿ < 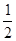при n ≥ N, x [0,1[. Зафиксируем в этом неравенстве n ≥ N и перейдем к пределу при x→1−0. Получим 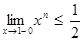. Тогда 1 ≤ 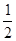. Противоречие. Значит,сходимость 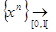f(x) = 0 не является равномерной. Это подтверждается и геометрической интерпретацией равномерной сходимости. На рисунке 7.4 видно, что при всех значениях n графики функций y = xⁿ выходят за пределы полосы .

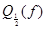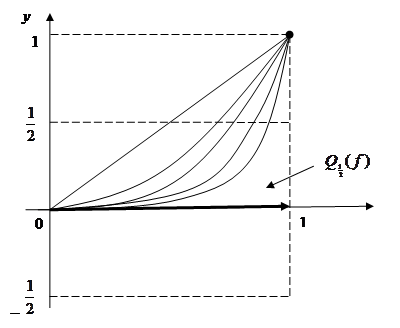
Рис. 7.4.