Функциональные ряды. Сходимость и равномерная сходимость функциональных рядов

Предположим, что на числовом множестве V задана функциональная последовательность {u_n(x)}. Тогда на множестве V определён функциональный ряд 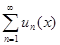, причём при каждом фиксированном x V соответствующий числовой ряд либо сходится, либо расходится.

Определение 1. Множество всех значений x, при которых сходится функциональный ряд 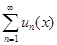, называется областью сходимости этого ряда.

Примеры. 1. Дан функциональный ряд .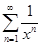

При любом x≠ 0 данный ряд является геометрической прогрессией, знаменатель которой равен 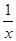. Следовательно, функциональный ряд 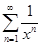сходится тогда и только тогда, когда 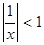. Значит, область сходимости этого ряда ]− ∞, −1[ 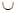]1, + ∞[.

2. Рассмотрим функциональный ряд 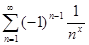. При каждом фиксированном x ]−∞,+∞[ числовой ряд 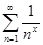является обобщённым гармоническим рядом, который сходится при x > 1. Следовательно, функциональный ряд 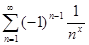сходится абсолютно при x > 1.

Если 0 < x < 1, то ряд 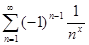удовлетворяет всем условиям теоремы Лейбница: 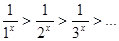, 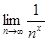= 0. Значит, данный функциональный ряд сходится условно при 0 < x <1.

Если же x ≤ 0, то 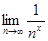≠ 0 и функциональный ряд 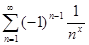расходится по необходимому признаку сходимости. Таким образом, область сходимости функционального ряда 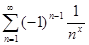– бесконечный интервал ]0, + ∞[, причём на интервале ]1, + ∞[ сходимость является абсолютной.

Пусть Ω – область сходимости функционального ряда 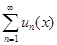. Если W Ω, то при любом x W ряд 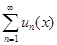сходится и, следовательно, имеет сумму S(x). В этом случае говорят, что функциональный ряд 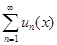сходится к функции S(x) на множестве W и пишут: 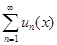= S (x) , где x W .

Пример. Имеет место равенство 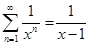, где

x ]− ∞, −1[ ]1, + ∞[. В самом деле, при x ]− ∞, −1[ ]1, + ∞[ геометрическая прогрессия 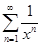имеет сумму

S(x) = .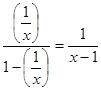

Из определения сходимости числового ряда следует, что функциональный ряд 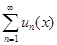сходится к функции S(x) на множестве W тогда и только тогда, когда последовательность частичных сумм {S_n(x)} ряда 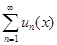сходится на множестве W к функции S(x), то есть {S_n(x)} 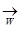S (x), где S_n(x) = 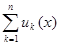, n N.

Определение 2. Функциональный ряд 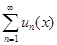сходится к функции S(x) равномерно на множестве W, если последовательность его частичных сумм {S_n(x)} сходится равномерно к функции S(x) на множестве W, т.е. {S_n(x)} 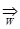S (x) .

Пример. Областью сходимости функционального ряда 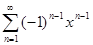является интервал ]− 1, + 1[ , причём

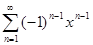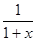= , x ]−1,+1[.

Докажем, что сходимость не является равномерной. Предположим, что ряд 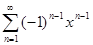сходится на интервале ]−1,+1[ равномерно. Тогда для ε = 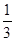найдётся номер N = N(ε) такой, что при всех n ≥ N одновременно для всех x ]−1,+1[ выполняется неравенство

|S_n(x) − S(x)| < ,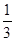

где S_n(x) = 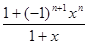, S(x) = 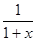. Значит, при n ≥ N и всех x ]−1,+1[ выполняется неравенство 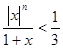. Зафиксируем в этом неравенстве n ≥ N и перейдём к пределу при x→1−0. Получим 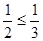. Полученное противоречие означает, что сходимость функционального ряда на интервале ]−1,+1[ не является равномерной.