Предельные признаки сходимости Даламбера и Коши
Теорема 5.1(признак сходимости Даламбера). Пусть дан числовой ряд 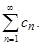 Предположим, что
Предположим, что 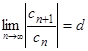 .
.
Если d < 1, то ряд 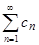 сходится абсолютно. Если d > 1, то этот ряд расходится.
сходится абсолютно. Если d > 1, то этот ряд расходится.
Доказательство. Пусть d < 1. Тогда найдется число ε > 0 такое, что q = d + ε < 1. Так как 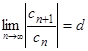 , то для ε > 0 существует номер N такой, что при всех n ≥ N выполняется неравенство
, то для ε > 0 существует номер N такой, что при всех n ≥ N выполняется неравенство
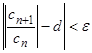 . Отсюда
. Отсюда 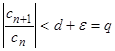 при всех n ≥ N. Тогда
при всех n ≥ N. Тогда 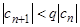 , где n ≥ N . Значит,
, где n ≥ N . Значит,
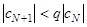 ,
,
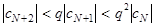 ,
,
................................
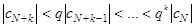 ,
,
................................
Числовой ряд
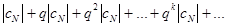
сходится, так как является геометрической прогрессией со знаменателем q , где 0 < q < 1. Ряд
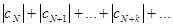
сходится, так как имеет сходящуюся мажоранту. Тогда сходится и ряд из модулей
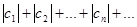 ,
,
так как сходится его остаток. Согласно теореме 4.1, исходный числовой ряд 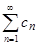 сходится, причем абсолютно.
сходится, причем абсолютно.
Пусть d > 1. Тогда найдется ε > 0 такое, что d − ε = q > 1. По условию 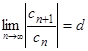 . Тогда для ε > 0 существует номер N такой, что при всех n ≥ N выполняется неравенство
. Тогда для ε > 0 существует номер N такой, что при всех n ≥ N выполняется неравенство 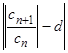 < ε. Отсюда
< ε. Отсюда 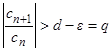 при всех n ≥ N. Тогда
при всех n ≥ N. Тогда 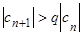 , где n ≥ N. Значит,
, где n ≥ N. Значит,
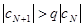 ,
,
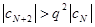 ,
,
................................
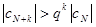 ,
,
................................
Так как q > 1, то последовательность {сn} является неограниченной. Значит, исходный числовой ряд 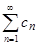 расходится по необходимому признаку сходимости.
расходится по необходимому признаку сходимости.
Замечание.Если в условиях теоремы 5.1. 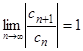 , то исходный ряд может как сходиться, так и расходиться. Например, ряд
, то исходный ряд может как сходиться, так и расходиться. Например, ряд 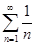 расходится, а ряд
расходится, а ряд 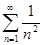 сходится. Однако
сходится. Однако
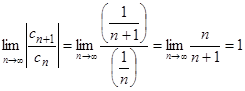 ,
,
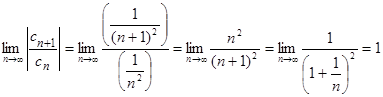 .
.
Пример. Рассмотрим числовой ряд 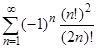 . Так как
. Так как
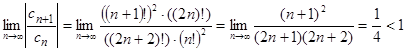 ,
,
то данный ряд сходится абсолютно по признаку Даламбера.
Теорема 5.2(предельный признак Коши). Пусть дан числовой ряд 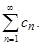 Предположим, что
Предположим, что 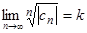 . Если k < 1, то ряд
. Если k < 1, то ряд 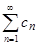 сходится абсолютно. Если k > 1, то ряд расходится.
сходится абсолютно. Если k > 1, то ряд расходится.
Доказательство.Пусть k < 1. Тогда существует число ε > 0 такое, что k + ε = q < 1. Так как 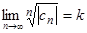 , то для ε > 0 найдется номер N такой, что
, то для ε > 0 найдется номер N такой, что 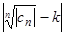 < ε при всех n
< ε при всех n 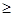 N. Отсюда
N. Отсюда
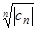 < k + ε = q при всех n ≥ N. Значит,
< k + ε = q при всех n ≥ N. Значит,
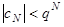 ,
,
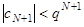 ,
,
………....
Отсюда следует, что ряд 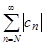 сходится, так как имеет сходящуюся мажоранту
сходится, так как имеет сходящуюся мажоранту 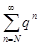 , где 0 < q < 1. Тогда будет сходиться и ряд
, где 0 < q < 1. Тогда будет сходиться и ряд 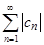 . По теореме 4.1, исходный числовой ряд
. По теореме 4.1, исходный числовой ряд 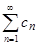 сходится, причем абсолютно.
сходится, причем абсолютно.
Пусть k > 1. Тогда найдется ε > 0 такое, что k − ε = q > 1. Так как 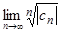 = k, то для числа ε > 0 существует номер N такой, что
= k, то для числа ε > 0 существует номер N такой, что 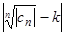 < ε при всех n ≥ N. Тогда
< ε при всех n ≥ N. Тогда 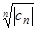 > k − ε = q при всех n ≥ N. Отсюда
> k − ε = q при всех n ≥ N. Отсюда
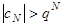 ,
,
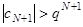 ,
,
...................
Так как q > 1, то последовательность {сn} является неограниченной. Тогда ряд 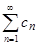 расходится по необходимому признаку сходимости.
расходится по необходимому признаку сходимости.
Пример.Исследуем на сходимость ряд 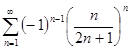 .
.
Так как 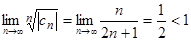 , то ряд сходится абсолютно.
, то ряд сходится абсолютно.
Замечание.Если 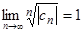 , то ряд
, то ряд 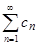 может как сходиться, так и расходиться. В самом деле, гармонический ряд
может как сходиться, так и расходиться. В самом деле, гармонический ряд 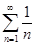 расходится, а ряд
расходится, а ряд 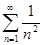 сходится. Однако
сходится. Однако
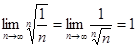 ,
, 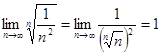 ,
,
так как 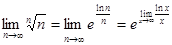 = 1.
= 1.
Задачи.
5.1. С помощью предельного признака Даламбера исследовать сходимость рядов:
а) 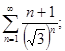 б)
б) 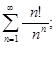 в)
в) 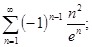
г) 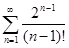 ; д)
; д) 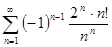 ; е)
; е) 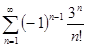 .
.
5.2. С помощью предельного признака Коши исследовать сходимость рядов:
а) 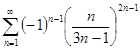 ; б)
; б) 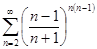 ;
;
в) 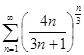 ; г)
; г) 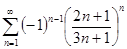 ;
;
д) 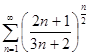 ; е)
; е) 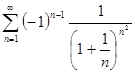 .
.
5.3. Исследовать сходимость рядов:
а) 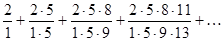 ;
;
б) 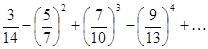 ;
;
в) 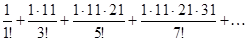 ;
;
г) 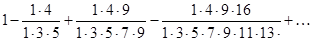 ;
;
д) 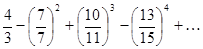 .
.
5.4. Доказать сходимость ряда 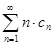 , если:
, если:
а) 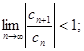 б)
б) 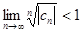 .
.
Дата добавления: 2016-07-09; просмотров: 1641;
