Признаки сходимости положительных рядов
Определение.Числовой ряд  называется положительным, если все его члены неотрицательны, то есть an ≥ 0, n
называется положительным, если все его члены неотрицательны, то есть an ≥ 0, n  N.
N.
Теорема 3.1(общий признак сходимости положительного ряда). Положительный числовой ряд  сходится тогда и только тогда, когда последовательность частичных сумм этого ряда ограничена сверху.
сходится тогда и только тогда, когда последовательность частичных сумм этого ряда ограничена сверху.
Доказательство необходимости.Если числовой ряд  сходится, то сходится последовательность его частичных сумм
сходится, то сходится последовательность его частичных сумм 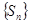 . Любая сходящаяся последовательность ограничена. Значит последовательность
. Любая сходящаяся последовательность ограничена. Значит последовательность 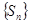 ограничена сверху.
ограничена сверху.
Доказательство достаточности.Дан положительный числовой ряд  , причем последовательность его частичных сумм
, причем последовательность его частичных сумм 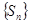 ограничена сверху. Так как
ограничена сверху. Так как
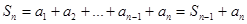 ,
,
где an ≥ 0, то 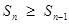 , n
, n  N. Это означает, что последовательность частичных сумм
N. Это означает, что последовательность частичных сумм 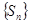 является неубывающей. Если неубывающая последовательность ограничена сверху, то она сходится. Значит, последовательность частичных сумм
является неубывающей. Если неубывающая последовательность ограничена сверху, то она сходится. Значит, последовательность частичных сумм 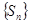 ряда
ряда  является сходящейся. Тогда сходится и сам ряд
является сходящейся. Тогда сходится и сам ряд  .
.
Пример.Дан числовой ряд 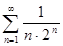 . Так как
. Так как
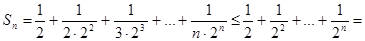
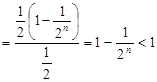 , n
, n  N,
N,
то последовательность частичных сумм ряда 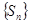 ограничена сверху. Согласно теореме 3.1, ряд сходится.
ограничена сверху. Согласно теореме 3.1, ряд сходится.
Определение. Числовой ряд 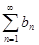 называется мажорантой положительного ряда
называется мажорантой положительного ряда 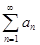 , если
, если 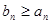 для всех n
для всех n  N.
N.
Первый признак сравнения. Если сходится мажоранта положительного ряда, то сходится и сам ряд. Если положительный ряд расходится, то расходится и любая его мажоранта.
Доказательство. Предположим, что ряд 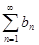 сходится и является мажорантой положительного ряда
сходится и является мажорантой положительного ряда 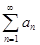 . Так как положительный ряд
. Так как положительный ряд 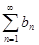 сходится, то последовательность его частичных сумм
сходится, то последовательность его частичных сумм 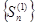 ограничена сверху, то есть
ограничена сверху, то есть 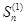 ≤ A, n
≤ A, n  N.
N.
По условию 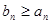 , n
, n  N. Тогда
N. Тогда
Sn = a1 + a2 + … + an ≤ b1 + b2 + … + bn = 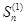 ≤ A, n
≤ A, n  N.
N.
Это означает, что последовательность частичных сумм 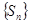 ряда
ряда 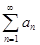 ограничена сверху. В силу общего признака сходимости положительного ряда, этот ряд сходится.
ограничена сверху. В силу общего признака сходимости положительного ряда, этот ряд сходится.
Второе утверждение доказывается методом от противного.
Пример. Исследуем на сходимость числовой ряд 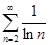 . Сначала покажем, что ln n < n при n ≥ 2. Для этого рассмотрим функцию f(x) = x – ln x, где х > 0.
. Сначала покажем, что ln n < n при n ≥ 2. Для этого рассмотрим функцию f(x) = x – ln x, где х > 0.
Эта функция непрерывна на множестве x ≥ 1. Ее производная равна 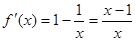 , причем
, причем 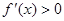 при всех x > 1. Значит, функция f(x) = x – ln x является возрастающей на множестве x ≥ 1. Тогда
при всех x > 1. Значит, функция f(x) = x – ln x является возрастающей на множестве x ≥ 1. Тогда 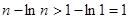 > 0 при n > 1. Отсюда
> 0 при n > 1. Отсюда  при n ≥ 2 и, следовательно,
при n ≥ 2 и, следовательно, 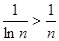 при n ≥ 2. Положительный ряд
при n ≥ 2. Положительный ряд  расходится, как остаток гармонического ряда
расходится, как остаток гармонического ряда 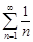 . Тогда расходится и его мажоранта
. Тогда расходится и его мажоранта 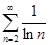 .
.
Второй признак сравнения. Пусть даны два положительных ряда 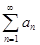 и
и 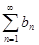 , где bn > 0, n
, где bn > 0, n  N. Тогда:
N. Тогда:
1) если 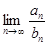 = 0,то из сходимости ряда
= 0,то из сходимости ряда 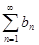 следует сходимость ряда
следует сходимость ряда 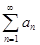 ;
;
2) если 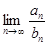 = ∞,то из расходимости ряда
= ∞,то из расходимости ряда 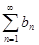 следует расходимость ряда
следует расходимость ряда 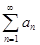 ;
;
3) если существует 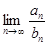 ≠ 0, то ряды
≠ 0, то ряды 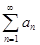 и
и 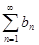 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Предположим, что существует предел 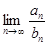 . Сходящаяся последовательность всегда ограничена. Значит, существует число λ > 0 такое, что
. Сходящаяся последовательность всегда ограничена. Значит, существует число λ > 0 такое, что 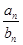 ≤ λ , n
≤ λ , n  N. Тогда
N. Тогда 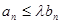 , n
, n  N. Если сходится ряд
N. Если сходится ряд 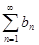 , то сходится и ряд
, то сходится и ряд 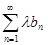 . Тогда будет сходиться и ряд
. Тогда будет сходиться и ряд 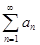 , так как имеет сходящуюся мажоранту
, так как имеет сходящуюся мажоранту  . Первое утверждение доказано.
. Первое утверждение доказано.
Если 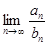 = ∞, то
= ∞, то 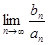 = 0. Рассуждая аналогичным образом и используя второе утверждение первого признака, получим, что из расходимости ряда
= 0. Рассуждая аналогичным образом и используя второе утверждение первого признака, получим, что из расходимости ряда 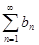 следует расходимость ряда
следует расходимость ряда 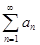 .
.
Наконец, если 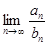 ≠ 0, то существует
≠ 0, то существует 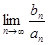 ≠ 0. Тогда из сходимости ряда
≠ 0. Тогда из сходимости ряда 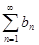 следует сходимость ряда
следует сходимость ряда 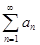 , а из сходимости ряда
, а из сходимости ряда 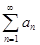 следует сходимость ряда
следует сходимость ряда 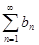 . Аналогичный вывод получаем и для расходящихся рядов. Таким образом, ряды сходятся или расходятся одновременно.
. Аналогичный вывод получаем и для расходящихся рядов. Таким образом, ряды сходятся или расходятся одновременно.
Пример. Рассмотрим числовой ряд 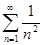 . Ранее было установлено, что ряд
. Ранее было установлено, что ряд 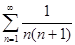 сходится. Так как
сходится. Так как
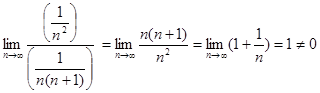 ,
,
то сходится и ряд 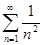 .
.
Теорема 3.2.(интегральный признак сходимости Коши). Пусть функция f(x)является неотрицательной и невозрастающей на промежутке [1, +∞[. Если
a1 = f (1), a2 = f (2),…, an = f (n), …,
то числовой ряд 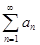 сходится тогда и только тогда, когда сходится несобственный интеграл
сходится тогда и только тогда, когда сходится несобственный интеграл  .
.
Доказательство. Если x  [k,k+1], то f(k+1) ≤ f(x) ≤ f(k). Значит, ak+1 ≤ f(x) ≤ ak, где k = 1, 2, …. Тогда
[k,k+1], то f(k+1) ≤ f(x) ≤ f(k). Значит, ak+1 ≤ f(x) ≤ ak, где k = 1, 2, …. Тогда
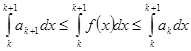 , k = 1, 2, ….
, k = 1, 2, ….
Отсюда
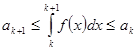 , k = 1,2, …
, k = 1,2, …
Предположим, что числовой ряд 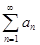 сходится. Это означает, что последовательность частичных сумм
сходится. Это означает, что последовательность частичных сумм 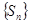 этого ряда ограничена сверху, то есть существует число А такое, что
этого ряда ограничена сверху, то есть существует число А такое, что 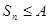 , n
, n  N. Рассмотрим функцию F(b) =
N. Рассмотрим функцию F(b) = 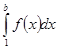 , где b ≥ 1. Так как по условию функция f(x) ≥ 0на множестве [1,+∞[, то F(b) − неубывающая функция. Значит, если b < N, где N − некоторое фиксированное натуральное число, то
, где b ≥ 1. Так как по условию функция f(x) ≥ 0на множестве [1,+∞[, то F(b) − неубывающая функция. Значит, если b < N, где N − некоторое фиксированное натуральное число, то
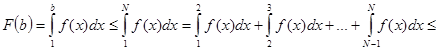
≤ a1 + a2 + …+ aN – 1 ≤ A.
Таким образом, F(b) ≤ A, где b ≥ 1. Так как неубывающая на множестве b ≥ 1 функция F(b) ограничена сверху на этом множестве, то существует 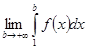 . Значит, интеграл
. Значит, интеграл 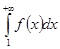 сходится.
сходится.
Предположим теперь, что сходится несобственный интеграл 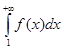 . Это означает, что функция
. Это означает, что функция 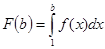 ограничена сверху, то есть существует число В такое, что
ограничена сверху, то есть существует число В такое, что 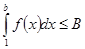 для любого b
для любого b  [1,+∞[ . Тогда
[1,+∞[ . Тогда
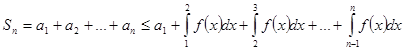 =
=
= a1 + 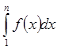 ≤ a1 + B, n
≤ a1 + B, n  N.
N.
Значит, последовательность частичных сумм 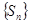 положительного ряда
положительного ряда 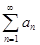 ограничена сверху. По теореме 3.1 ряд сходится.
ограничена сверху. По теореме 3.1 ряд сходится.
Пример. Числовой ряд 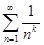 называется обобщенным гармоническим рядом. При k = 1 мы имеем гармонический ряд
называется обобщенным гармоническим рядом. При k = 1 мы имеем гармонический ряд 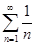 . При k ≤ 0 ряд
. При k ≤ 0 ряд 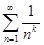 расходится в силу необходимого признака сходимости. Если
расходится в силу необходимого признака сходимости. Если 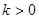 , то функция f(x) =
, то функция f(x) = 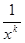 является неотрицательной и невозрастающей на множестве x ≥ 1, причем
является неотрицательной и невозрастающей на множестве x ≥ 1, причем
f (1) = 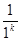 , f (2) =
, f (2) = 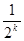 , …, f (n)=
, …, f (n)= 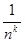 ,… . Несобственный интеграл
,… . Несобственный интеграл 
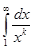 сходится при
сходится при 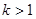 и расходится при
и расходится при 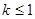 . По теореме 3.2 ряд
. По теореме 3.2 ряд 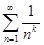 сходится при
сходится при 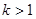 и расходится при
и расходится при 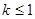 .
.
Задачи.
3.1. Используя общий признак сходимости положительных рядов, доказать сходимость числового ряда  , если:
, если:
а) a n = 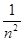 , n
, n  N; б) a n =
N; б) a n = 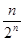 , n
, n  N; в) a n =
N; в) a n = 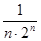 , n
, n  N.
N.
3.2. Доказать, что ряд 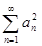 сходится, если сходится положительный ряд
сходится, если сходится положительный ряд  .
.
3.3. Исследовать сходимость положительного ряда:
а) 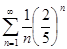 ; б)
; б) 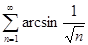 ;
;
в) 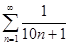 ; г)
; г) 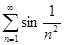 ;
;
д) 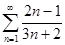 ; е)
; е) 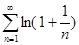 ;
;
ж)  ; з)
; з) 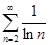 ;
;
и) 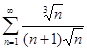 ; к)
; к) 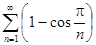 .
.
3.4. Исследовать сходимость ряда с помощью интегрального признака Коши:
а) 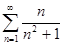 ; б)
; б) 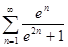 ; в)
; в) 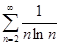 ;
;
г) 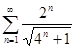 ; д)
; д) 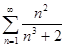 ; е)
; е) 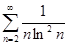 ;
;
ж) 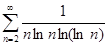 ; з)
; з) 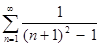 .
.
3.5. Исследовать, при каких p сходится числовой ряд:
а) 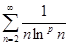 ; б)
; б) 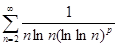 ; в)
; в) 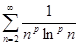 .
.
Дата добавления: 2016-07-09; просмотров: 8596;
