Теорема про симетричність функції Гріна самоспряженої крайової задачі.
Теорема. Функція Гріна самоспряженої крайової задачі є симетричною : 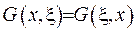 .
.
Доведення. Нехай маємо самоспряжену крайову задачу
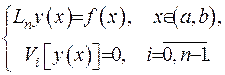 (2.58)
(2.58)
За ознакою самоспряженої крайової задачі випливає, що:
1) 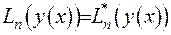 , тобто диференціальний оператор задачі є самоспряженим.
, тобто диференціальний оператор задачі є самоспряженим.
2) Виконується інтегральна умова для двох функцій, що задовольняють крайовій задачі (2.58):
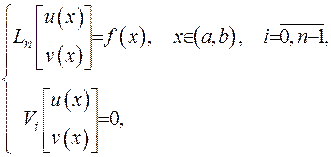
а саме
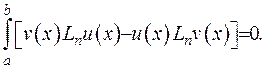 (2.59) Функція Гріна для обох розв’язків є однаковою
(2.59) Функція Гріна для обох розв’язків є однаковою
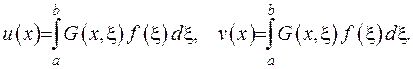
Тоді, підставляючи ці вирази до співвідношення (2.59), отримаємо наступну рівність:
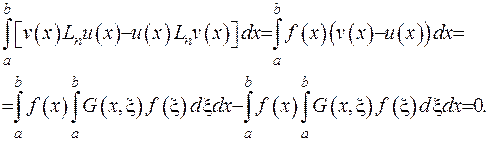 (2.60)
(2.60)
Можна записати ці повторні інтеграли, як подвійні:
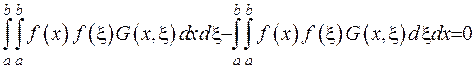 . (2.61)
. (2.61)
У першому доданку виразу (2.61) змінимо порядок інтегрування:
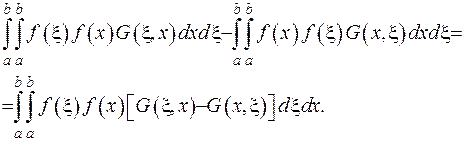
З цього випливає рівність
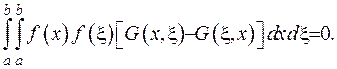 (2.62)
(2.62)
Зведемо позначення 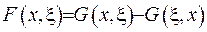 , за допомогою якого висновок (2.62) запишемо у вигляді:
, за допомогою якого висновок (2.62) запишемо у вигляді:
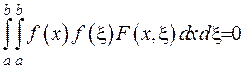 . (2.63)
. (2.63)
З рівності інтеграла нулю ще не випливає, що 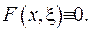 Доведемо це, проводячи доведення теореми від протилежного. Нехай
Доведемо це, проводячи доведення теореми від протилежного. Нехай 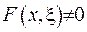 , тоді існує деяка точка
, тоді існує деяка точка 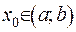 така, що
така, що 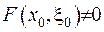 , та, наприклад,
, та, наприклад, 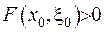 . Оскільки розв’язок крайової задачі, зображений через функцію Гріна, може бути застосований для будь-якої неперервної функції
. Оскільки розв’язок крайової задачі, зображений через функцію Гріна, може бути застосований для будь-якої неперервної функції 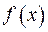 , маємо право вибрати її наступним чином. Припустимо, що
, маємо право вибрати її наступним чином. Припустимо, що 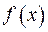 відмінна від нуля в околі деякої точки
відмінна від нуля в околі деякої точки 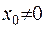 , а зовні цієї окрестности вона дорівнюватиме нулеві:
, а зовні цієї окрестности вона дорівнюватиме нулеві: 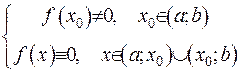 . Аналогічну поведінку має функція
. Аналогічну поведінку має функція 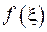 в околі точки
в околі точки 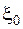 . Такий вибір функцій базується на тому, що розв’язок існує для будь-якої неперервної функції у правій частині диференціального рівняння. У такому випадку, не обмежуя загальності міркувань, можемо вважати, що
. Такий вибір функцій базується на тому, що розв’язок існує для будь-якої неперервної функції у правій частині диференціального рівняння. У такому випадку, не обмежуя загальності міркувань, можемо вважати, що 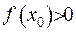 та
та 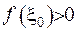 . Тоді рівність (2.63) прийме вигляд
. Тоді рівність (2.63) прийме вигляд
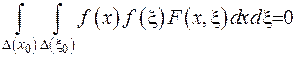 .
.
Під інтегралом тут стоїть функція, значення якої у точці 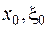 , є додатнім
, є додатнім 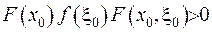 . Отже, інтеграл від неї у лівій частині рівності має бути додатнім
. Отже, інтеграл від неї у лівій частині рівності має бути додатнім 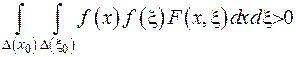 .
.
Отримали протиріччя, з якого випливає, що функція 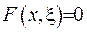 , а з цього, у свою чергу, випливає, що
, а з цього, у свою чергу, випливає, що 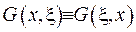 .
.
Дата добавления: 2016-05-05; просмотров: 785;
