Выражение оператора Лапласа в ортогональной КСК.
Чтобы получить выражение 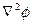 в ортогональной КСК, воспользуемся определением:
в ортогональной КСК, воспользуемся определением:
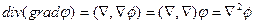 . Выразим
. Выразим 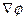 в ортогональной КСК по формуле (7.8), тогда
в ортогональной КСК по формуле (7.8), тогда 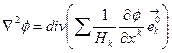 . Если компоненты градиента подставить в формулу (7.16), то
. Если компоненты градиента подставить в формулу (7.16), то
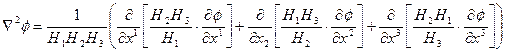 (7.22)
(7.22)
Это и есть искомое выражения оператора Лапласа в ортогональной КСК.
Подведем итог по всей лекции. Выбор той или иной системы координат определяется
соображениями удобства или симметрией решаемой задачи. Наиболее простой и естественной является ДСК, в которой ФМФГ имеет вид единичной матрицы:
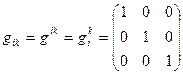 (7.23)
(7.23)
из которого видно, что все коэффициенты Ламе тождественно равны единице. Для задания произвольной КСК необходимо задать либо координатные преобразования (5.4), либо определить все компоненты ФМТГ. В ортогональной КСК достаточно знать три функции 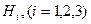 . Очевидно, что в КСК работать сложнее, чем в ДСК. Это хорошо видно на примере основных векторных операций. Иногда симметрия задачи такова, что использование ДСК становится невыгодным. В этом случае удобной может оказаться ортогональная КСК. Однако бывают задачи, в которых учитывается кривизна пространства ( Римановы пространства). Для такого случая невозможно записать ДСК во всем пространстве и приходится пользоваться произвольными КСК. В этой лекции мы записали выражения основных операций векторного анализа в ортогональной криволинейной системе координат. Очевидно, что вид этих операций можно получить в любой КСК, однако из-за громоздкости мы не станем их приводить. Предоставим эту возможность читателю.
. Очевидно, что в КСК работать сложнее, чем в ДСК. Это хорошо видно на примере основных векторных операций. Иногда симметрия задачи такова, что использование ДСК становится невыгодным. В этом случае удобной может оказаться ортогональная КСК. Однако бывают задачи, в которых учитывается кривизна пространства ( Римановы пространства). Для такого случая невозможно записать ДСК во всем пространстве и приходится пользоваться произвольными КСК. В этой лекции мы записали выражения основных операций векторного анализа в ортогональной криволинейной системе координат. Очевидно, что вид этих операций можно получить в любой КСК, однако из-за громоздкости мы не станем их приводить. Предоставим эту возможность читателю.
Упражнение 7
1. Вычислить градиенты скалярных полей в цилиндрических координатах.
a) 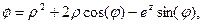
b) 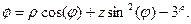
2. Вычислить градиенты скалярных полей в сферических координатах.
a) 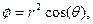
b) 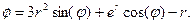
3. Вычислить дивергенцию векторных полей в цилиндрических координатах.
a) 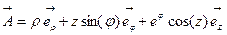 ,
,
b) 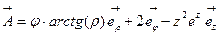 .
.
4. Вычислить дивергенцию векторных полей в сферических координатах.
a) 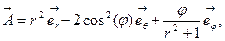
b) 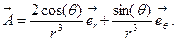
5. Вычислить ротор векторных полей в криволинейных координатах.
a) 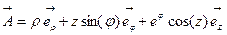
b) 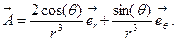
c) 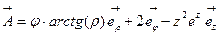
d) 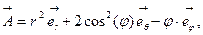
6. Записать в сферической и цилиндрической системах координат выражения для оператора Лапласа 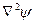 .
.
Дата добавления: 2016-10-17; просмотров: 965;
