Выражение градиента в ортогональной КСК

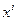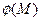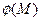Рассмотрим одну из координатных линий , как кривую в области D, в которой задано скалярное поле . Согласно определению, нормированный базисный вектор направлен по касательной прямой к этой линии в точке M. Воспользуемся определением градиента (1.8) и запишем связь его с производной от поля по направлению , тогда ,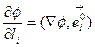

где 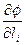- производная по направлению соответствующей координатной линии в точке M Разложим градиент в ортонормированном базисе КСК: 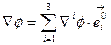(7.5)

Здесь 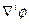- компоненты градиента. После подстановки получим

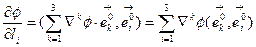
или, учитывая определение ортонормированности базиса, (7.6)

Из полученного равенства следует, что производная от 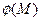по направлению координатной линии совпадает с проекцией градиента, так как она имеет требуемую размерность и называется физической компонентой вектора. По определению 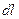- расстояние между двумя бесконечно близкими точками и по формуле (7.3) оно равно 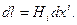(7.7)

После подстановки (7.7) в (7.6), получим 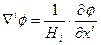, или окончательно

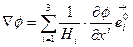. (7.8)

Это и есть искомое выражение градиента в ортонормированной КСК. Следует обратить внимание на формулу (7.7), так как она позволяет дать геометрическую интерпретацию коэффициентов Ламе. В левой части равенства (7.7) стоит расстояние между двумя точками на координатной линии, в правой - разность координат этих точек, следовательно, коэффициенты Ламе переводят разность координат в расстояние вдоль соответствующей координатной линии. Таким образом, с помощью коэффициентов 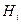можно вычислить длину линии, площадь поверхности и объем тела в ортогональной КСК.

Аналогичные рассуждения справедливы и в контравариантном базисе. Если же учесть, что оба базиса взаимно обратны, т.е. соответствующие вектора взаимно перпендикулярны, то для ортонормированных КСК различия в базисах исчезают и расположение индексов у компонент векторов может быть произвольным (обычно индексы пишут внизу).