Метрика криволинейной системы координат

Построение векторного анализа в произвольной КСК предполагает знание формулы, задающей расстояние между двумя точками пространства. При этом достаточно задать расстояние между двумя бесконечно близкими точками. В ДСК не было никаких затруднений, поскольку расстояние в ней определялось формулой Евклида (5.2). В КСК этот вопрос менее простой и требует детального рассмотрения.

Определим квадрат расстояния между двумя бесконечно близкими точками инвариантным

(не зависящим от выбора системы координат) способом, как квадрат длины (модуль) вектора 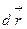соединяющего эти точки: 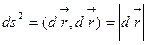. (6.10)

Расписав скалярное произведение (6.10) в ДСК, мы получим формулу Евклида (6.1). Представим 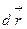например, в ковариантном базисе КСК по формуле (6.6), тогда:

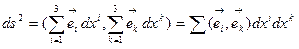
ОПРЕДЕЛЕНИЕ 6.3. Множество функций 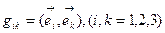(6.11)

называется Фундаментальным Метрическим Тензором Гаусса (ФМТГ) в ковариантной форме.

В теории пространств этот набор (тензор) играет важную роль и определяет метрику пространства. Используя определение 6.3, получим 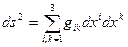(6.12) Фундаментальную Метрическую Форму Гаусса (ФМФГ), задающую расстояние для двух бесконечно близких точек в ковариантном базисе КСК через разности их координат. Аналогичные формулы легко получить в контравариантном базисе:

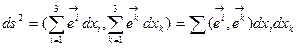
ОПРЕДЕЛЕНИЕ 6.4. Множество функций 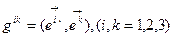, (6.13)

называется Фундаментальным Метрическим Тензором Гаусса (ФМТГ) в контравариантной форме.

Запишем ФМФГ в контравариантном базисе. 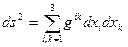, (6.14)

Имеется еще одна возможность задать ФМФГ и ФМТГ, если вектор 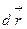представить один раз в ковариантном базисе, а другой раз в контравариантном, тогда

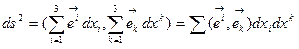
ОПРЕДЕЛЕНИЕ 6.5. Множество функций 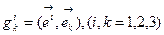, (6.15)

называется Фундаментальным Метрическим Тензором Гаусса (ФМТГ) в смешанной форме.

Формула расстояния в смешанном базисе примет вид: 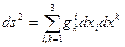(6.16)

Такое многообразие способов задания расстояния в КСК может вызвать по началу некоторую растерянность у читателя, однако не следует отчаиваться. Важно усвоить следующее: система координат - это один из способов математического отображения различных физических величин. Выбор координатной сетки достаточно произволен и этот произвол не должен влиять на физические законы. Поэтому для определения метрики в КСК безразличен выбор того или иного базисов, т.к. 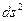имеет одно и тоже значение в любом представлении. Принципиальным здесь является задание девяти функций ФМТГ .

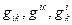Получим выражение ФМТГ в произвольной КСК, если заданы координатные преобразования

(6.3) и (6.4). Для этого запишем формулу для расстояния в ДСК 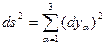(6.17)

вычислим 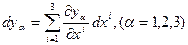(6.18)

Подставим (6.18) в (6.17) и поменяем порядок суммирования (запомните: при умножении сумм индексы суммирования должны быть разными)

.

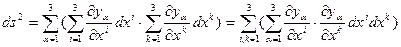Сравнивая это выражение с формулой (6.12), приходим к выводу, что

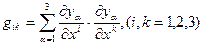(6.19)

Это и есть искомое выражение компонент ФМТГ в ковариантной форме в произвольной КСК. Таким образом для получения явного вида 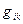в той или иной КСК необходимо задать координатные преобразования между ДСК и КСК.