Построение криволинейной системы координат

В предыдущих лекциях мы часто обращались к декартовой системе координат (ДСК), в то время как существует множество других координатных сеток. И это вполне оправдано, так как ДСК - наиболее простая и естественная система координат. Она представляет собой три взаимно перпендикулярные, попарно пересекающиеся плоскости, общая точка пересечения - начало ДСК, линии пересечения - координатные оси (см. рис. 6).

Рис. 6 Разложение вектора в ДСК

Если каждую точку на координатных осях занумеровать, приписав ей число, равное расстоянию этой точки до начала ДСК, мы осуществим их естественную градуировку и декартовы координаты будут иметь метрическую размерность. ДСК будет полностью определена, если ее сориентировать в пространстве, выделив на осях направления положительных и отрицательных значений декартовых координат. Осуществить это можно с помощью тройки единичных базисных векторов

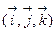помещенных в начало ДСК и касательных к координатным осям. Произвольный вектор

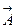будет иметь следующее стандартное разложение в ДСК: 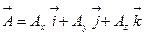. Проекции этого вектора связаны с декартовыми координатами, задающими начальную и конечную точку 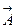, по формулам: 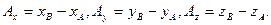Важным свойством ДСК является то, что для описания любых величин и процессов в ней достаточно ввести одну глобальную систему координат с произвольным началом и фиксированным базисом.

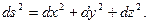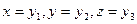Расстояние между двумя бесконечно близкими точками совпадает с разностью координат этих точек, если они расположены на оси координат, или выражается через них по формуле Евклид: В дальнейшем, для удобства записи громоздких выражений, введем знак суммы и все координаты будем нумеровать индексами. Так для ДСК введем обозначения т.е. 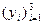- декартовы координаты. Тогда формула расстояния в ДСК примет вид: 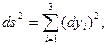(6.1)

где 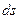- расстояние между двумя бесконечно близкими точками, 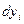-разность их декартовых координат.

Построим произвольную Криволинейную Систему Координат (КСК), опираясь на ДСК. Рассмотрим в ДСК три поверхности, которые пересекаются только попарно и имеют хотя бы одну общую точку. Пусть эти поверхности заданы следующей системой уравнений:

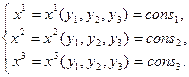(6.2)

По аналогии с ДСК линии пересечения поверхностей будем называть координатными линиями, общую точку пересечения - началом КСК. Из определения поверхности следует, что на координатной линии две функции из (6.3) будут постоянными, а третья будет принимать некоторые числовые значения. Этими числами можно занумеровать все точки координатной линии и они будут играть роль криволинейных координат (см. рис. 7.).

Рис. 7. Криволинейная система координат

Таким образом, каждой точке на координатной линии соответствует определенное число из области значений соответствующей функции: 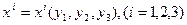. Это значит, что КСК проградуирована. Для описания векторных величин, КСК необходимо сориентировать в пространстве, т.е. задать базисные вектора. Из линейной алгебры известно, что для этого достаточно определить тройку линейно независимых векторов. Поступим следующим образом, наряду с ДСК рассмотрим полярную систему координат, когда точки пространства нумеруются с помощью радиуса-вектора 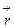. Уравнения (6.2) задают криволинейные координаты 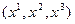как функции декартовых и называются координатными преобразованиями. Будем считать эти преобразования не вырожденными и запишем обратный переход от криволинейных к декартовым:

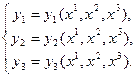(6.3)

С помощью обратного преобразования (6.4) выразим радиус-вектор в КСК:

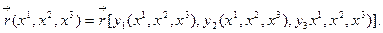
Вычислим дифференциал радиус-вектора 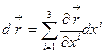(6.4)

Тройка векторов 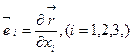, (6.5)

построенных в начале КСК, линейно независима и может быть выбрана в качестве базиса КСК.

ОПРЕДЕЛЕНИЕ 6.1. Тройка линейно независимых векторов (6.6) называется ковариантным базисом КСК

По определению частной производной вектор 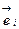направлен по касательной прямой к соответствующей координатной линии, т.е. базисные вектора 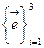ориентированы по касательному направлению к координатным линиям. Формулу (6.4) следует рассматривать как правило разложения произвольного вектора в ковариантном базисе КСК: 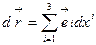(6.6)

причем набор чисел 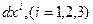принято называть контравариантными компонентами вектора, в данном случае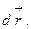

Рассмотрим вопрос о единственности выбора базиса КСК. Криволинейные координаты

задаются уравнениями (6.2), их можно рассматривать как поверхности равного уровня для скалярного поля 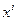(см. лекцию 1). Построим тройку векторов 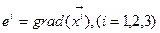(6.7)

Известно, что градиент всегда ортогонален к ПРУ, следовательно, вектора (6.7) не компланарны и

ориентированы перпендикулярно координатным поверхностям. По этому они могут также рассматриваться в качестве базиса КСК.

ОПРЕДЕЛЕНИЕ 6.2 Тройка линейно независимых векторов (6.7) называется контравариантным базисом КСК}.

Таким образом, в криволинейной системе координат имеются по крайней мере две возможности ввести базисные вектора: ковариантные (6.5) и контравариантные (6.7). В общем случае ни тот, ни другой базисы не обладают каким-либо преимуществом, однако на практике выбор их диктуется соображениями удобства или симметрией решаемой задачи. К тому же в дальнейшем мы увидим, что использование смешанного базиса во многом упрощает запись громоздких выражений. Правило разложения (6.4) можно распространить и на контравариантный базис: 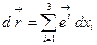(6.8)

При этом надо иметь ввиду , что криволинейные проекции одного и того же вектора в разных базисах в общем случае различны. Чтобы это учесть, компоненты вектора в контравариантном базисе будем называть ковариантными и обозначать индексами внизу. Такая нелогичность в названиях проекций вектора в дальнейшем получит свое объяснение. На данном этапе необходимо запомнить правила разложения любого вектора в обоих базисах: 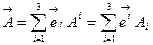(6.9)

Таким образом, мы предлагаем читателям запомнить, что компоненты произвольного вектора в ковариантном базисе обозначаются индексами вверху и называются контравариантными, а компоненты вектора в контравариантном базисе обозначаются индексами внизу и называются ковариантными. Другими словами, положение индекса у проекции вектора определяет в каком базисе она получена.