Нормировка базиса КСК
Рассмотрим вопрос о нормировке базисных векторов в КСК. Известно, что орты ДСК 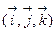 безразмерны, ортогональны и нормированы на единицу. Ковариантный и контравариантный базисы КСК, в общем случае, имеют произвольную размерность, не ортогональны и не нормированы. Осуществить нормировку и, следовательно, сделать базис КСК безразмерным можно следующим образом. Определим единичный ковариантный базисный вектор
безразмерны, ортогональны и нормированы на единицу. Ковариантный и контравариантный базисы КСК, в общем случае, имеют произвольную размерность, не ортогональны и не нормированы. Осуществить нормировку и, следовательно, сделать базис КСК безразмерным можно следующим образом. Определим единичный ковариантный базисный вектор
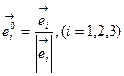 (6.20)
(6.20)
где 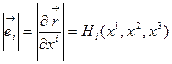 (6.21)
(6.21)
масштабные множители Ламе (геометрический смысл этих множителей мы выясним позже). Таким образом, связь не нормированного и нормированного базисных векторов будет иметь вид:
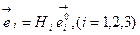 (6.22)
(6.22)
Аналогичная нормировка имеет место и для контравариантного базиса:
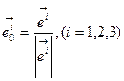 (6.23)
(6.23)
где 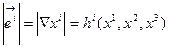 (6.24)
(6.24)
дифференциальные множители Ламе (геометрический смысл и этих множителей мы также выясним позже). И в этом случае связь ненормированного и нормированного базисных векторов будет иметь вид: 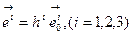 , (6.25)
, (6.25)
Разложим вектор 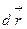 в ковариантном базисе по формуле (6.6) и подставим в формулу:
в ковариантном базисе по формуле (6.6) и подставим в формулу:
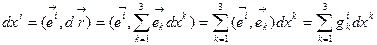 (6.26)
(6.26)
Распишем сумму в (6.26) для 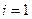 , тогда
, тогда 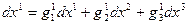 , очевидно, что в данном случае мы имеем линейную зависимость между компонентами вектора
, очевидно, что в данном случае мы имеем линейную зависимость между компонентами вектора 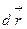 . Это противоречит
. Это противоречит
теореме о единственности разложения вектора в базисе. Чтобы устранить это противоречие, необходимо потребовать для 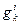 следующие свойства:
следующие свойства:
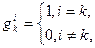
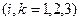
Тогда мы имеем тождество 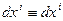 , а
, а 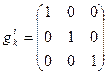 представляет собой единичную матрицу.
представляет собой единичную матрицу.
Упражнение 6
Построить цилиндрическую систему координат: координатные поверхности, координатные
линии, базисные вектора, компонентны ФМТГ, коэффициенты Ламе, записать 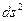 , если заданы координатные преобразования вида:
, если заданы координатные преобразования вида:
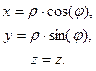
1. Построить сферическую систему координат: координатные поверхности, координатные линии, базисные вектора, компонентны ФМТГ, коэффициенты Ламе, записать 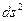 , если заданы координатные преобразования вида:
, если заданы координатные преобразования вида:
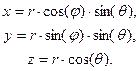
Дата добавления: 2016-10-17; просмотров: 1205;
