Выражение ротора в ортогональной КСК

Рассмотрим произвольную ортонормированную КСК ( см. рис.9).

Рис. 9. Вычисление ротора в КСК

Для получения выражения ротора в этой системе координат, воспользуемся формулой, связывающей плотность циркуляции с проекцией ротора на нормаль (3.4). Если замкнутый контур

определить так, как указано на рис. 9., то в качестве нормали можно выбрать соответствующий базисный вектор 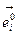. Так, например, для криволинейного параллелограмма OACB базисный вектор 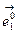c точностью до второго порядка малости ортогонален к площадке, ограниченной контуром OACB. В этом случае, используя свойство (3.4), запишем:

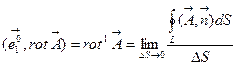. (7.17)

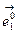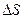Здесь - проекция ротора на орт , - площадка, ограниченная контуром OACB, 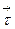- единичный вектор касательный к этому контуру. Чтобы вычислить предел (7.17), необходимо подсчитать циркуляцию вектора 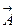вдоль OACB, задавая направление обхода против часовой стрелки. Очевидно, что контурный интеграл равен

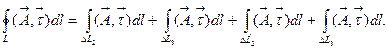
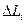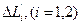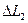
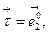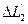
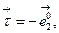С принятой точностью на криволинейных отрезках и , справедливы следующие утверждения: на на 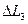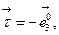на на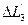

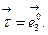
С помощью теоремы Лагранжа о среднем получим:

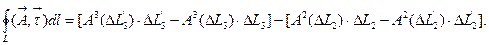
В данном случае мы обозначили 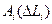- проекции вектора 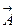на орт 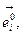в некоторой точке на криво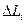й или 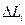. Разность в круглых скобках будем рассматривать как приращение функции при переходе с отрезка 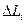на отрезок 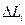. Тогда, используя формулу (7.17), получим

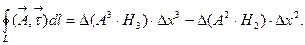
Подставим полученное значение интеграла в формулу (7.17) и выразим площадь криволинейного параллелограмма в ортогональной КСК: 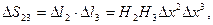тогда

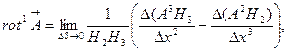или, используя определение частной производной,

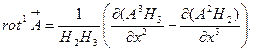(7.18)

Оставшиеся две компоненты ротора также легко получить, если замкнутые криволинейные контуры выбрать на соответствующих координатных поверхностях (читатель может проделать это самостоятельно):

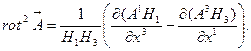(7.19)

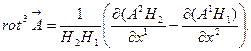(7.20)

Полное выражение вектора ротора в ортогональной КСК имеет громоздкий вид и его

удобней представить в виде определителя:

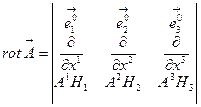(7.21)