Операция перемещения индексов.
ОПРЕДЕЛЕНИЕ 9.3. Операцией поднятия или опускания индексов называется правило, позволяющее преобразовывать компоненты тензора из одного типа в другой.
Введем эту операцию на примере вектора 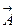 (тензора первой валентности). Представим
(тензора первой валентности). Представим 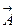 в противоположных базисах:
в противоположных базисах: 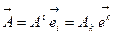 . Умножим это равенство скалярно на
. Умножим это равенство скалярно на 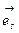 и воспользуемся определением ФМТГ в ковариантной и смешанной формах, тогда
и воспользуемся определением ФМТГ в ковариантной и смешанной формах, тогда 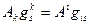
Сумму 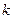 вычислим, если воспользуемся свойством
вычислим, если воспользуемся свойством 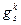 .
.
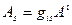 (9.5.)
(9.5.)
Формула (9.5) связывает ковариантные и контравариантные компоненты вектора 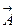 и называется операцией опускания индекса, т.к. она позволяет вычислить проекции вектора с нижними индексами по проекциям с верхними индексами. Очевидно, что обратная ей операция поднятия индекса будет иметь следующий вид:
и называется операцией опускания индекса, т.к. она позволяет вычислить проекции вектора с нижними индексами по проекциям с верхними индексами. Очевидно, что обратная ей операция поднятия индекса будет иметь следующий вид:
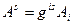 (9.6.)
(9.6.)
Обобщим эту операцию на многовалентные тензора, например 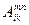 . Представим
. Представим 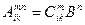 , множитель
, множитель 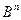 преобразуем по формуле (9.6.), тогда
преобразуем по формуле (9.6.), тогда
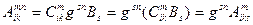 (9.7.)
(9.7.)
Это операция однократного поднятия индекса 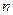 . Применим ее еще раз для второго индекса. Для
. Применим ее еще раз для второго индекса. Для
этого представим снова 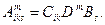
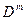 и
и 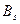 преобразуем по формуле (9.6.).
преобразуем по формуле (9.6.).
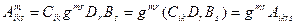 (9.8.)
(9.8.)
Подставим это вычисление в формулу (9.7) 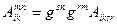 (9.9.)
(9.9.)
Так выглядит операция двукратного поднятия индексов.
Общее правило поднятия и опускания любого числа индексов. Чтобы передвинуть некоторое число индексов, необходимо компоненты исходного тензора умножить на компоненты ФМТГ столько раз, сколько индексов преобразуется и каждое произведение просуммировать по повторяющимся противоположными индексам.
Приведем пример операции четырехкратного опускания индексов.
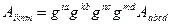
Дата добавления: 2016-10-17; просмотров: 857;
