Геодезические линии

Из геометрии Евклида мы знаем, что в плоском пространстве кратчайшее расстояние между двумя точками - это прямая линия. Основным признаком прямой линии служит то, что ее длина является минимальной по сравнению с любой кривой, соединяющей те же точки. Оказалось, что в любых метрических пространствах существуют линии, обладающие минимальной длинной. Их принято называть геодезическими линиями.

ОПРЕДЕЛЕНИЕ 11.3. Линия, соединяющая две точки пространства 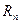и имеющая наименьшую длину по сравнению с любой другой, проходящей через эти же точки, называется геодезической.

Вывод дифференциального уравнения, основанного на определении 11.3, требует знаний

вариационного исчисления. Поэтому мы воспользуемся другим свойством геодезической линии: при параллельном переносе единичного касательного вектора вдоль геодезической он остается постоянным, т.е. ковариантная производная от его компонент равна нулю. Правда, откровенно следует сказать, что сам процесс параллельного переноса вектора в пространстве Римана теряет свою наглядность и становится неоднозначным. К сожалению, у нас нет иного выхода, как ограничится этим замечанием в надежде на любознательность читателя.

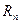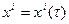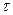Рассмотрим в линию, задаваемую параметрическими уравнениями , где - произвольный параметр. Из математического анализа известно, что 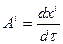- вектор касательный к данной линии. Нормируем этот вектор на единицу, вводя новый параметр .

.

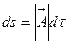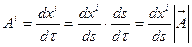Отсюда 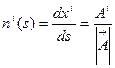. Вычислим ковариантную производную от 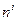и приравняем ее нулю.

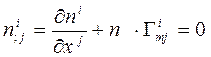
Умножим это равенство на 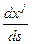и просуммируем по .

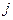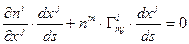
Учитывая зависимость 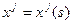и формулу вычисления сложной производной,

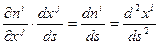
окончательно получим

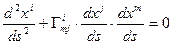(11.5)

Формула (11.5) задает дифференциальное уравнение геодезической линии в римановых пространствах. Если пространство Евклида рассматривать как частный случай риманового с кривизной равной нулю, то в нем всегда можно ввести ДСК, где все 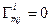и уравнение (11.5) принимает вид: 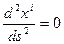. Решением этого уравнения является прямая линия, задаваемая системой параметрических уравнений: .

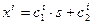Упражнение 11

1. Вывести уравнение геодезической линии, пользуясь определением геодезической как кривой экстремальной длины.

2. Найти символы Кристоффеля и компоненты тензора кривизны в 2-мерном пространстве вида:

a) ,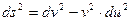

b)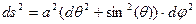

3. Вычислить в ортонормированном базисе тензор кривизны для метрики:

,

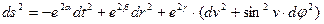где 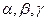- функции от .

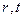Найти для этой метрики тензор Риччи, скалярную кривизну и тензор Эйнштейна.

Рекомендуемая литература:

1. Пчелин Б. К. Векторный анализ. -- М., 1969.

2. Краснов М. Л. и др. Векторный анализ. -- М., 1978.

3. Фомин А. В., Будак В. Г. Кратные интегралы и ряды. -- М., 1967.

4. Кухлинг Х. Справочник по физике .... -- М., 1982.

5. Кочин К. Е. Векторное исчисление и начала тензорного исчисления.-- М., 1957.

6. Рашевский П. К. Тензорный анализ и риманова геометрия. -- М., 1967

7. Дубровин Б. А. Современная геометрия -- М., 1979.

8. Мак -- Конелл Дж. Введение в тензорный анализ. -- М., 1969.