Операция понижения валентности тензора.

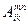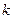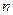Операция понижения валентности тензора называется сверткой индексов. Введем эту операции на примере тензора вида . Общее число компонент у этого тензора 81 штука. Выберем среди них те, у которых значения индексов и совпадают, и просуммируем их:

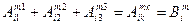(9.10.)

Тензор 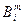называется сверткой тензора .

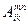ОПРЕДЕЛЕНИЕ 9.4. Однократой сверткой тензора называется тензор, полученный путем суммирования компонент исходного тензора по двум одинаковым значениям противоположных индексов.

Очевидно, что операцию свертки можно повторить для следующей пары противоположных индексов, т.е. двукратно. Например, для 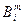при 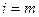имеем .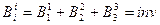

Учитывая формулу (9.10), двукратная свертка выглядит следующим образом

Свойства.

1. В результате однократной свертки валентность тензора понижается на две единицы.

2. Сворачивать тензор (в общем случае) необходимо по противоположным индексам.

3. Если тензор представлен в ковариантной или контравариантной формах, то сначала необходимо перейти к смешанной форме, применяя операцию поднятия или опускания индексов.

3. С помощью достаточного числа сверток тензор четной валентности приводится к инварианту (тензору нулевой валентности), а тензор нечетной валентности – к тензору первой валентности (вектору).

Докажем корректность операции свертки. Для этого предварительно рассмотрим следующую лемму.

Лемма. Пусть в любой КСК заданы 9 чисел 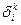, принимающих следующее значение:

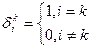(9.11.)

Тогда совокупность 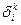образует смешанный тензор второй валентности - тензор Кронекера.

Докажем необходимое условие. Предположим, что 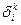тензор, тогда для него справедлив тензорный закон:

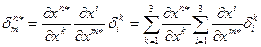(9.12.)

Используя свойство (9.11), вычислим сумму по 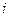в (9.12): .

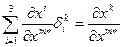По формуле сложной производной свернем сумму по :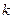

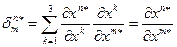(9.13)

Таким образом, если 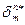- тензор, обладающий свойством (9.11), то его компоненты всегда можно представить в виде (9.13) в любой КСК. Это утверждение становится очевидным, если вспомнить, что координаты линейно независимы между собой. В старой КСК имеем:

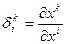(9.14.)

Докажем достаточное условие. Пусть набор чисел (9.11) задается формулами (9.13) и (9.14), определим для него закон преобразования. Из формулы (9.13) следует:

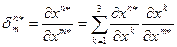
Учитывая зависимость между КСК, по формуле сложной производной запишем:

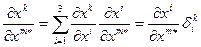
Окончательно, опуская знак суммы, 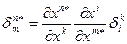получим тензорный закон преобразования смешанного тензора второй валентности.

Проверим корректность операции свертки на примере тензора 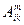. Тензорный закон для него следующий: 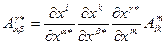. Образуем свертку в новой КСК по индексам и :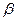

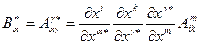
Выделим сумму по и свернем ее (см. лемму):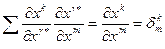

После подстановки сумма по 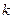элементарно просчитывается: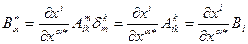

Таким образом, в результате однократной свертки мы получили тензор на две единицы меньшей валентности: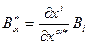

В заключение этой лекции еще раз отметить, что не надо пугаться громоздких выражений с многократными суммами. Необходимо преодолеть робость перед ними и запомнить основные правила работы, в чем и заключается залог успеха.

Упражнение 9

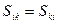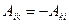1. Показать, что если тензор - симметричный ( ), а тензор - антисимметричный ( ), то 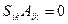. Вывести следующие два тождества, справедливые для

произвольного тензора :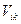

, и .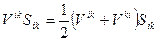

2. Доказать, что сумма диагональных компонент тензора второй валентности 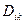(шпур тензора 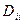) является инвариантом.

3. Доказать, что тензор второй валентности антисимметричный (симметричный) в одной системе координат, антисимметричный (симметричный) во всех других системах координат.

4. Показать, что если в некоторой системе координат соответствующие компоненты двух векторов пропорциональны, то они пропорциональны в любой другой системе координат.