Дифференцирование тензоров
В математическом анализе вводится понятие частной производной в ДСК от какой-либо функции, например, от компоненты вектора, как предел следующего вида:
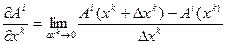 (10.15)
(10.15)
Чтобы построить аналогичную операцию в произвольной КСК, предварительно проверим частную производную (10.15) на корректность. Так как 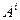 контравариантный тензор первой валентности, то для него справедлив тензорный закон:
контравариантный тензор первой валентности, то для него справедлив тензорный закон:
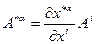
Продифференцируем его по 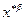 :
:
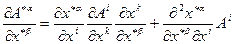 (10.16)
(10.16)
Если ввести обозначения
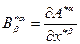 ,
, 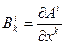
то для частной производной от компоненты вектора получим закон преобразования
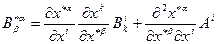 (10.17)
(10.17)
который не совпадает с тензорным. Это означает, что в КСК операция частного дифференцирования не корректна, и необходимо построить дифференциальную операцию от тензора таким образом, чтобы она не выводила из поля тензоров, т.е. снова давала тензор и в ДСК совпадала с обычной частной производной. Чтобы выполнить эту задачу, осмыслим сначала, почему несправедлив тензорный закон для частной производной от компоненты вектора. Дело в том, что приращение 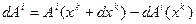 содержит в себе не только истинное изменение проекции как полевой величины, но и фиктивное изменение, связанное с локальностью базиса КСК. Вопрос становится еще более запутанным и сложным, если задуматься над тем, каким образом можно сравнить компоненты одного и того же вектора в двух бесконечно близких точках. В ДСК эта задача решается с помощью параллельного переноса вектора из одной точки в другую. Для КСК понятие параллельного переноса становится не тривиальной процедурой и, вообще говоря, определяется не однозначно, так как результат параллельного переноса зависит в общем случае от выбора пути перемещения вектора. К сожалению, мы не готовы обсуждать эту проблему
содержит в себе не только истинное изменение проекции как полевой величины, но и фиктивное изменение, связанное с локальностью базиса КСК. Вопрос становится еще более запутанным и сложным, если задуматься над тем, каким образом можно сравнить компоненты одного и того же вектора в двух бесконечно близких точках. В ДСК эта задача решается с помощью параллельного переноса вектора из одной точки в другую. Для КСК понятие параллельного переноса становится не тривиальной процедурой и, вообще говоря, определяется не однозначно, так как результат параллельного переноса зависит в общем случае от выбора пути перемещения вектора. К сожалению, мы не готовы обсуждать эту проблему
потому, что она выходит за рамки нашего курса и требует специальных знаний по теории пространств. Здесь мы только констатируем тот факт, что в КСК реальное изменение компонент вектора 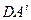 как функции точки можно получить путем вычитания из полного изменения
как функции точки можно получить путем вычитания из полного изменения 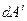 фиктивное изменения
фиктивное изменения 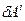 , связанное с локальностью КСК, т.е.
, связанное с локальностью КСК, т.е. 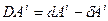 или, учитывая (10.14)
или, учитывая (10.14)
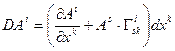 (10.18)
(10.18)
Формулу (10.18) можно рассматривать как определение дифференциала от компоненты вектора в КСК, а выражение, стоящее в скобках - обобщением производной на КСК.
ОПРЕДЕЛЕНИЕ 10.2. Ковариантной производной от контравариантной проекции вектора называется дифференциальная операция вида:
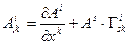 (10.18)
(10.18)
Аналогичные рассуждения позволяют построить ковариантную производную для ковариантной компоненты вектора. Воспользуемся контравариантным базисом КСК и формулами (10.13) и (10.14), тогда
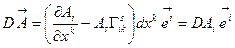
ОПРЕДЕЛЕНИЕ 10.3. Ковариантной производной от ковариантной компоненты вектора называется дифференциальная операция вида:
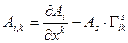 (10.19)
(10.19)
Обобщим понятие ковариантной производной на тензор любой валентности. При этом потребуем, чтобы правила дифференцирования, известные нам из математического анализа, были справедливы в КСК, что является вполне естественным: они не должны зависеть от выбора системы координат. Рассмотрим 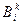 и, не ограничивая общности, представим его в виде
и, не ограничивая общности, представим его в виде  , вычислим ковариантную производную от произведения.
, вычислим ковариантную производную от произведения.
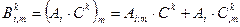
Для 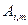 применим формулы (10.19), а для
применим формулы (10.19), а для  - (10.18):
- (10.18):
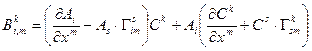
Раскроем скобки и перегруппируем слагаемые соответствующим образом.
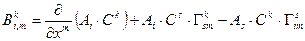 . Окончательно ковариантная производная от смешанного тензора второй валентности будет вычисляться по следующей формуле:
. Окончательно ковариантная производная от смешанного тензора второй валентности будет вычисляться по следующей формуле:
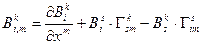 (10.20)
(10.20)
Очевидно, что для тензоров большей валентности выражение ковариантной производной становится еще более громоздким. Читатель сам в этом может легко убедится, если построит ковариантную производную от тензора третей валентности. Здесь мы приведем только результат этого построения.
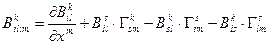 (10.21)
(10.21)
Следует еще раз напомнить, что по повторяющимся индексам ведется суммирование.
Обсудим вопрос о системах координат. Нам известно, что в ДСК все 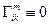 , поэтому ковариантная производная переходит в частную производную. Однако в дальнейшем мы увидим, что выбор ДСК не всегда целесообразен, а то и невозможен, в этом случае приходится учитывать локальность КСК и все вытекающие из этого последствия: недиагональность метрики, не тензорный характер частной производной и т.д. Более подробно об этом мы остановимся в последней лекции или же можно прочитать в [6].
, поэтому ковариантная производная переходит в частную производную. Однако в дальнейшем мы увидим, что выбор ДСК не всегда целесообразен, а то и невозможен, в этом случае приходится учитывать локальность КСК и все вытекающие из этого последствия: недиагональность метрики, не тензорный характер частной производной и т.д. Более подробно об этом мы остановимся в последней лекции или же можно прочитать в [6].
Упражнение 10
1. Доказать, что ковариантная производная от компонент ФМТГ в любой системе координат тождественно равна нулю.
2. Вычислить все символы Кристоффеля первого рода на сфере радиуса 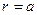 (двумерная криволинейная система координат).
(двумерная криволинейная система координат).
3. Для метрики Шварцшильда
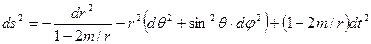
записать компоненты ФМТГ и вычислить все символы Кристоффеля первого рода.
4. Доказать следующие тождества:
a) 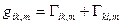 , где
, где 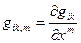
b) 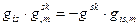 , где
, где 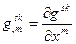
c) 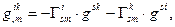
d) 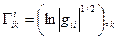
5. Доказать, что в координатном репере с диагональным ФМТГ символы Кристоффеля определяются соотношениями:
a) 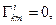 при
при 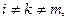
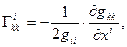
b) 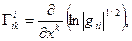
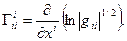
Дата добавления: 2016-10-17; просмотров: 2242;
