ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ ФУНКЦИЙ

Рассмотрим неявное уравнение 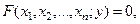которое кратко запишем в виде:

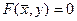. (6)

Теорема 3.(о существовании, непрерывности и дифференцируемости неявной

функции). Если выполнены следующие условия:

1. существует точка 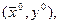в которой выполнено уравнение (6)

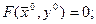
2. функция 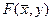дифференцируема в некоторой окрестности точки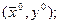

3. частная производная 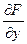непрерывна в точке 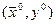и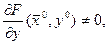

то в некоторой окрестности точки 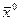существует единственная функция 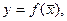которая является решением уравнения (6), причем в точке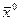 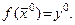Функция 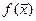непрерывна и дифференцируема в окрестности точки 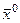, и ее частные производные в этой точке вычисляются по формулам:

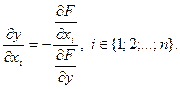(7)

Отметим два частных случая.

1. Если кривая 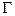задана неявно уравнением 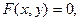то 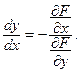Эта формула содержит второй способ вычисления производной 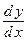неявной функции.

2. Если поверхность 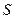задана неявно уравнением 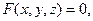то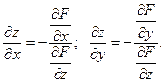

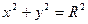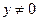Например, на окружности при и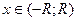

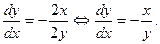
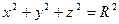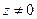На сфере при и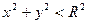

КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ,

ЗАДАННОЙ НЕЯВНО

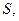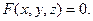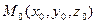
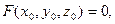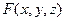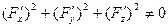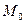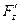Рассмотрим поверхность заданную неявно уравнением Полагаем, что в точке в окрестности этой точки функция дифференцируема, причем в точке и непрерывна в этой точке. Тогда на основании теоремы о неявной функции уравнение 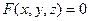определяет в некоторой окрестности точки 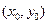однозначную дифференцируемую функцию 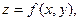удовлетворяющую уравнению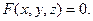

Назовем касательной плоскостью к поверхности 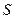в точке 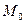плоскость, описываемую уравнением:

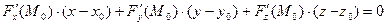. (8)

Нормаль – это прямая, проходящая через точку 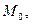перпендикулярно к касательной плоскости. Ее уравнение имеет вид:

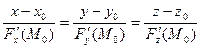. (9)

Вектор 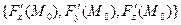является направляющим вектором нормали и равен градиенту функции 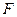в точке 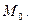Этот вектор перпендикулярен касательной плоскости и, соответственно, перпендикулярен поверхности 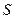в точке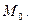

Отсюда следует, что 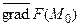перпендикулярен поверхности уровня 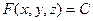функции 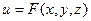в точк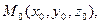е где 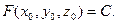Это свойство называют ортогональным свойством градиента.

Если поверхность задана явно уравнением 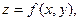то его следует переписать в виде 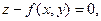ввести функцию 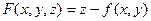и составить уравнения касательной плоскости и нормали по формулам (5.25) и (5.26).

Пример 4. Написать уравнения касательной плоскости и нормали к поверхности 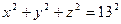в точке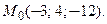

□ Введем функцию 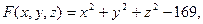тогда уравнение поверхности примет вид: 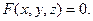Найдем частные производные:

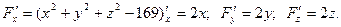
В точке 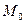частные производные и градиент соответственно равны: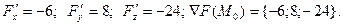

Касательная плоскость описывается уравнением:

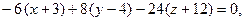
которое после упрощений принимает вид: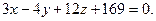

Уравнение нормали имеет вид: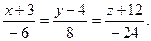

З а м е ч а н и е.В разделе 5.1.3 сфера 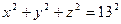была получена как поверхность уровня функции 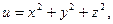проходящая через точку 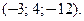Градиент 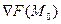является направляющим вектором нормали и перпендикулярен и касательной плоскости, и поверхности уровня в этой точке. ■