ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ Ф.Н.П.
Рассмотрим функцию 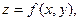 определенную и дифференцируемую в окрестности точки
определенную и дифференцируемую в окрестности точки 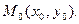 Тогда в этой окрестности существуют частные производные
Тогда в этой окрестности существуют частные производные 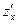 и
и  являющиеся функциями двух переменных
являющиеся функциями двух переменных 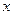 и
и 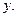
Частной производной второго порядка 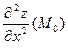 функции
функции 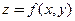 в точке
в точке 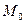 называют частную производную по
называют частную производную по 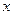 от частной производной
от частной производной  , вычисленную в точке
, вычисленную в точке 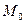 :
: 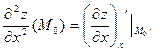
Частной производной второго порядка 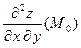 называют частную производную по
называют частную производную по 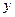 от частной производной
от частной производной  в точке
в точке 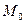 :
: 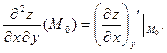
Аналогично вводят понятия частных производных 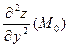 и
и 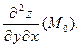 Используют и сокращенную форму записи производных:
Используют и сокращенную форму записи производных: 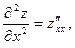
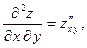
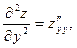
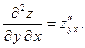
Частные производные 2-го порядка (если они существуют) являются функциями двух переменных 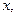
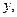 которые в свою очередь можно дифференцировать как по
которые в свою очередь можно дифференцировать как по 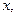 так и по
так и по 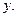
Получаем «дерево» частных производных высших порядков:
Частные производные, полученные дифференцированием функции по наборам разных переменных, называют смешанными.
Теорема 1. (о смешанных производных).Если функция 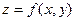 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 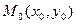 смешанные производные
смешанные производные 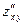 и
и 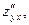 непрерывные в точке
непрерывные в точке 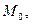 то
то 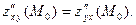
Из теоремы 1 следует независимость смешанных производных от порядка дифференцирования. Это теорема обобщается на функции произвольного числа переменных и смеша 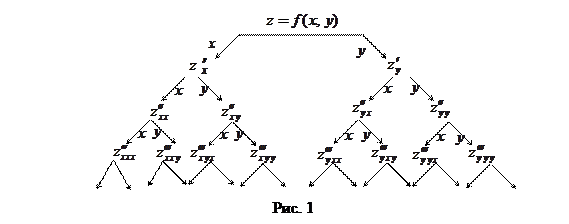
нные частные производные любых порядков, больших единицы.
Для иллюстрации этой теоремы рассмотрим пример.
Пример 1. Найти частные производные 3-го порядка 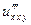 и
и  функции
функции

□ Используя «дерево» частных производных, получаем:
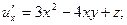
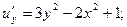
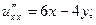


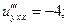
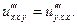
Заметим, что 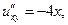 функции
функции 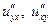 − непрерывные. Поэтому
− непрерывные. Поэтому 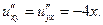 ■
■
Пусть функция 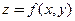 определена и имеет частные производные до
определена и имеет частные производные до 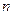 -го порядка включительно в окрестности точки
-го порядка включительно в окрестности точки 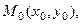 причем в точке
причем в точке 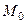 все частные производные непрерывны. В этом случае первый дифференциал
все частные производные непрерывны. В этом случае первый дифференциал 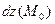 определен и вычисляется по правилу «цепочки»:
определен и вычисляется по правилу «цепочки»:

Введем оператор дифференцирования 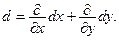 Тогда последнюю формулу можно переписать в виде:
Тогда последнюю формулу можно переписать в виде: 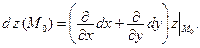
Дифференциал является функцией четырех переменных: 
Дифференциалом 2-го порядка функции 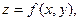 называется дифференциал дифференциала первого порядка:
называется дифференциал дифференциала первого порядка:
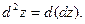
Дифференциал 3-го порядка – это дифференциал дифференциала 2-го порядка:
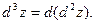
Продолжая рассуждения, введем дифференциал  -го порядка как дифференциал дифференциала
-го порядка как дифференциал дифференциала 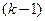 -го порядка:
-го порядка:
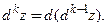
Если 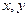 – независимые переменные, то в точке
– независимые переменные, то в точке 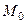
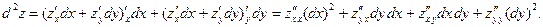
Если частные производные  непрерывны в точке
непрерывны в точке 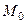 , то
, то 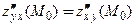 и формула для вычисления второго дифференциала принимает вид:
и формула для вычисления второго дифференциала принимает вид:
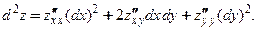 (1)
(1)
С помощью оператора дифференцирования 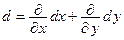 формулу (1) можно переписать в виде:
формулу (1) можно переписать в виде:
 .
.
Аналогично для функций, имеющих непрерывные частные производные  -го порядка включительно, имеем:
-го порядка включительно, имеем:
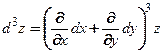 ,
,

Формула вычисления дифференциала произвольного порядка обобщается на функцию 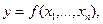 имеющую непрерывные частные производные до
имеющую непрерывные частные производные до  -го порядка включительно:
-го порядка включительно:
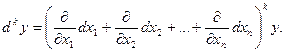
Пример 2. Найти второй дифференциал функции 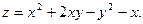
□ Функция  и все ее частные производные являются непрерывными функциями. Вычисляем все частные производные до 2-го порядка включительно:
и все ее частные производные являются непрерывными функциями. Вычисляем все частные производные до 2-го порядка включительно:
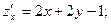
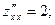
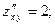
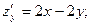

Найденные производные подставляем в формулу (1):
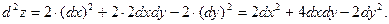 ■
■
Дата добавления: 2016-05-25; просмотров: 958;
