ФОРМУЛА ТЕЙЛОРА ДЛЯ Ф.Н.П.
Теорема 2.(Тейлора).Пусть функция 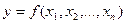 определена в некоторой окрестности
определена в некоторой окрестности  точки
точки  и имеет непрерывные частные производные до
и имеет непрерывные частные производные до 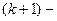 го порядка включительно в этой окрестности. Тогда для любой точки
го порядка включительно в этой окрестности. Тогда для любой точки  найдется промежуточная точка
найдется промежуточная точка  такая, что имеет место равенство:
такая, что имеет место равенство:
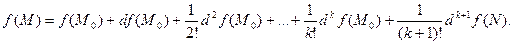 (2)
(2)
Эта формула называется формулой Тейлора 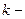 го порядка, а точка
го порядка, а точка 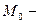 центром разложения. Последнее слагаемое называют остаточным членом формулы Тейлора. Остаточный член может быть записан в виде:
центром разложения. Последнее слагаемое называют остаточным членом формулы Тейлора. Остаточный член может быть записан в виде: 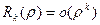 при
при 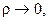 где
где  расстояние между точками
расстояние между точками 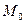 и
и 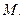 Точка
Точка  некоторая точка отрезка
некоторая точка отрезка 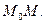 Все предшествующие слагаемые в правой части формулы образуют многочлен Тейлора
Все предшествующие слагаемые в правой части формулы образуют многочлен Тейлора 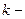 го порядка.
го порядка.
Рассмотрим частный случай формулы Тейлора.
Формула Тейлора 1-го порядка с центром в точке 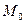 имеет вид:
имеет вид:
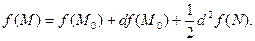 (3)
(3)
Для функции двух переменных 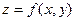

где 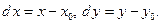
Подставив дифференциалы в формулу (5.20), получим
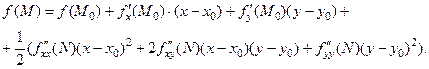 (4)
(4)
Для функции 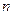 переменных
переменных 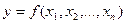 формула Тейлора 1-го порядка имеет вид:
формула Тейлора 1-го порядка имеет вид:
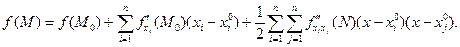 (5)
(5)
Формула Тейлора применяется при доказательствах теорем и в приближенных вычислениях значений производных, интегралов, при нахождении пределов функций.
Пример 3.Найти приближенное значение функции 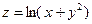 в точке
в точке 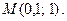
□ Запишем формулу Тейлора 1-го порядка для функции двух переменных в виде:
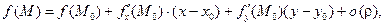
в качестве центра разложения выбрав точку 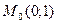 , так как в этой точке известно точное значение функции:
, так как в этой точке известно точное значение функции:  Тогда
Тогда 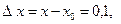
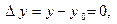

Находим частные производные 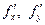 и вычисляем их значения в точке
и вычисляем их значения в точке 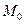 :
:
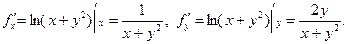
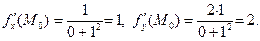
Подставляем 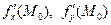 в формулу Тейлора 1-го порядка:
в формулу Тейлора 1-го порядка:
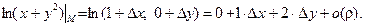
При 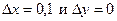 получаем:
получаем: 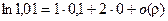 , или
, или 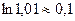 .■
.■
Дата добавления: 2016-05-25; просмотров: 1079;
