Приближенное дифференцирование функций

8.1 Цель работы

Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу» Приближенное дифференцирование», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.

8.2 Задание

Построить зависимости производных первого и второго порядка от аргумента в диапазоне 1..10 с единичным шагом.

Определить оптимальное значение шага, обеспечивающее минимальную погрешность приближенных расчетов производных первого и второго порядков для x=3.

Примеры заданий:

1) y=5x⁵+4x³ 2) y=x⁴ 3) y=e^x 4) y=2x³+x⁴ 5) y=x³+x⁵

6) y=x⁵ 7) y=x²+x⁴ 8) y=x³+x⁴ 9) y=e^2x 10) y=x³

8.3 Теоретические сведения

Задача приближенного дифференцирования возникает для сложных аналитических функций или функций , заданных дискретными данными. Функция приближенно описывается интерполяционным полиномом, дифференцирование которого не вызывает трудностей.

Таблица 8.1

x_i	y_i	Δy	Δ²y	Δ³y	Δ⁴y	Δ⁵y
x₀	y₀	Δy₀	Δ²y₀	Δ³y₀	Δ⁴y₀	Δ⁵y₀
x₁	y₁	Δy₁	Δ²y₁	Δ³y₁	Δ⁵y₁
x₂	y₂	Δy₂	Δ²y₂	Δ³y₂
x₃	y₃	Δy₃	Δ²y₃
x₄	y₄	Δy₄
x₅	y₅

Представим любую исходную функцию в виде таблицы 8.1 соответствующих значений x_i и y_i и конечных разностей Δy_i , Δ²y_i, Δ³y_i….В таблице конечные разности различных порядков рассчитываются по формулам

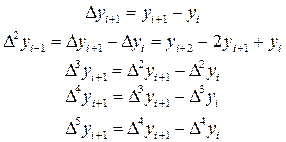(8.1)

Запишем интерполяционный полином в форме Ньютона :

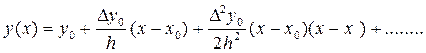(8.2)

Продифференцируем (8.2) по x :

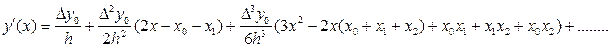(8.3)

Продифференцируем (8.3) по x :

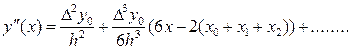(8.4)

При x=x₀

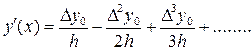
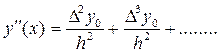(8.5)

Ограничиваясь только первым членом в разложениях ,получим

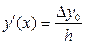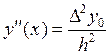; (8.6)

В случае h=1 формулы еще больше упрощаются и производные численно равны соответствующим конечным разностям

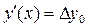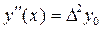; (8.7)

При уменьшении величины шага погрешность расчетов уменьшается. Наилучшая точность , которая может быть достигнута при уменьшении шага по оси x , определяется погрешностью округления, зависящей от используемого программного и аппаратного обеспечения.

Если при расчетах производных не ограничиваться только первыми членами суммы, то можно получить более точные формулы для расчета производных, учитывающие информацию не только о соседней, но и о более удаленных точках.

Для двух слагаемых( трехточечная схема) формулы (8.5) можно привести к виду

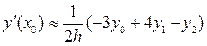
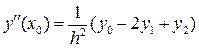(8.8)

Можно получить ещё более точные формулы, использую информацию о большем количестве точек. В этих случаях интерполяционный полином удобнее записывать в форме Лагранжа .

Для пятиточечной системы имеем

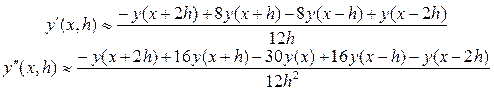(8.9)

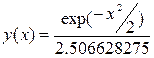Рассмотрим функцию

. (8.10)

При x=0.5 и h=0.01 получаем

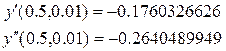
Процедура определения производной в Mathcad дает значения

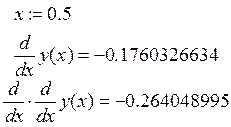
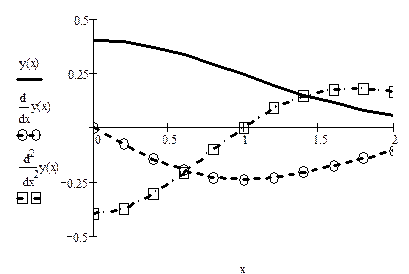
Рис.8.1 Графики функции (8.10) и её производных

На рисунке 8.1 показаны графики при x=0..2 при шаге h=0.01.

Результаты расчетов в зависимости от шага h имеют различную относительную ошибку.

-1 -3 -5 -7

lg(Δ)

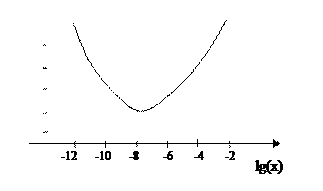
Рис. 8.2

На рисунке 8.2 показана зависимость абсолютной ошибки первой производной от величины шага h для функции y(x)=x³ при x=3.

При шаге h=10^-8достигается минимальная ошибка вычислений . Методическая погрешность убывает с уменьшением шага. При этом погрешность округления с уменьшением шага увеличивается, поэтому оптимальная величина суммарной погрешности вычислений достигается при h=10^-8.

Для численного дифференцирования в Mathcad используется метод Риддера, в котором для оценки точности производной последовательно определяются конечные разности высоких порядков. Максимальная степень оператора однократного вычисления производной равна пяти.

Для вычисления производных порядка >5 следует использовать смешенную запись.

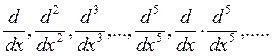
Для получения производной в символьном виде нужно записать оператор численного определения производной и затем поставить знак → из меню символьных вычислений , также можно использовать команду «Дифференцировать» из меню Символика.

8.4 Порядок выполнения работы

- получить у преподавателя задание на выполнение работы.

- ознакомиться с разделом 8.3 Теоретические сведения.

- рассчитать погрешности определения первой и второй производных в интервале x=1 до x=10 с шагом , равным 1, для одного и двух членов разложения интерполяционного полинома по формуле Ньютона , при помощи оператора дифференцирования Mathcad и оформить полученные результаты в виде таблиц и графиков.

- рассчитать зависимость погрешности вычисления производной от величины шага при x=3, в диапазоне h=10ⁱ, где i=-15..0

8.5 Пример выполнения работы

Выполним задание №10 F(x)=x³.

Рассчитаем конечные разности для h=1.

Диапазон изменения по x от 1 до 10 .

x	y	Δy	Δ²y	Δ³y	Δ⁴y

Точные значения производных y′=3x² , y″=6x .

Сравнение погрешностей определения первой и второй производных приведены в таблице 8.3.

Таблица 8.3

			y′(x)				y″(x)
x	y	точное знач-е	прибл. знач-е	абс. ошибка	отн. ошибка	точное знач-е	прибл. знач-е	абс. ошибка	отн. ошибка
					1,33				1,00
					0,58				0,50
					0,37				0,33
					0,27				0,25
					0,21				0,20
					0,18				0,17
					0,15				0,14
					0,13				0,13
					0,12

Погрешности определения производных в таблице 8.3 достаточно велики . Для их снижения необходимо уменьшить шаг h или использовать при расчете производных большим количеством элементов в разложениях (8.2) и (8.3).

Выполнение задания в Mathcad.

Записываем начальные данные .

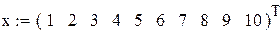
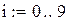
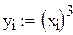
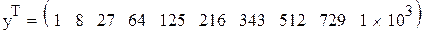
Конечная разность первого порядка

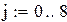
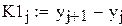
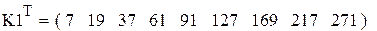
Трехточечная схема для первой производной

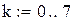
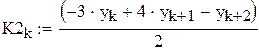
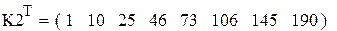
Форма записи или получения ответов в виде транспонированных строк удобна в случае большого количества элементов в столбце.

Точное решение с помощью оператора

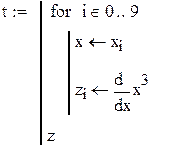
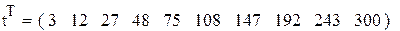
Сведем все полученные данные в таблицу

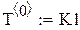
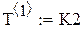
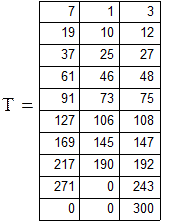
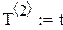
Построим сравнительный график для всех полученных величин

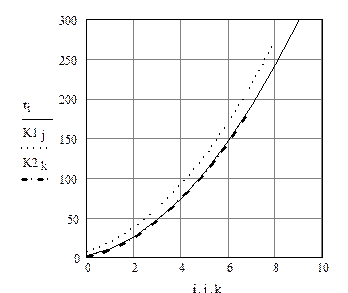
Рис.8.3 График точного значения производной, первой конечной разности и производной, полученной по трехточечной схеме

Из полученных результатов следует, что точность расчета первой производной по формуле конечной разности составляет 25%, для трехточечной схемы точность возрастает , а использование оператора дифференцирования в данном случае обеспечивает практически идеальное совпадение с точными результатами.

Теперь определим погрешность численного дифференцирования при различных шагах h.

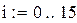
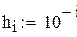
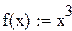
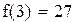
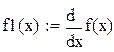
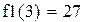
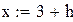
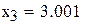
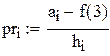
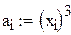
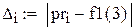
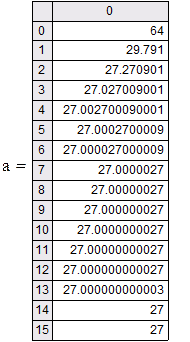
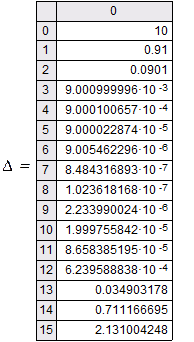
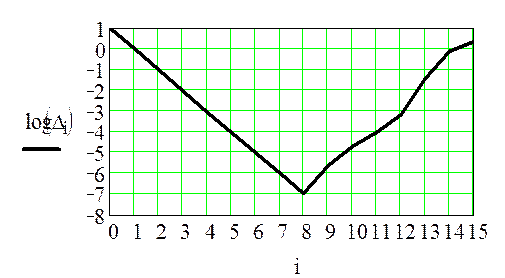
График зависимости удобнее строить в десятичных логарифмах исследуемых величин, поскольку нам важна степень результата.

Рис.8.4 Погрешность расчета производной при различном шаге h

Производная функции f(x)=x³ при x=3 может быть определена по формуле первой конечной разности с максимальной точностью 10^-7 при шаге h=10^-8.

8.6 Содержание отчета

1. Титульная страница с названием работы.

2. Задание.

3. Назначение работы и краткие теоретические сведения.

4. Результаты ручных расчетов в форме таблиц.

5. Методика и результаты машинных расчетов в форме таблиц.

6. Графические зависимости относительной погрешности от величины шага.

7. Выводы.

<== предыдущая лекция	\|	следующая лекция ==>
Другие экологические классификации и группы организмов	\|	Антропогенный фактор как группа экологических факторов, возникшая вследствие человеческой деятельности. Его характеристика и влияние на живые системы

Дата добавления: 2016-08-08; просмотров: 2279;