Связь символов Кристофелля с метрическим тензором

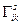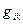Существование зависимости между и следует из того, что оба множества связаны с выбором базиса КСК. Чтобы получить эту зависимость, воспользуемся формулой (10.2). Домножим это выражение скалярно на 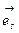и введем соответствующие компоненты ФМТГ.

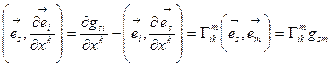(10.6)

Равенство (10.6) симметрично по индексам 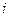и 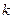, меняя их местами, получим еще одно уравнение:

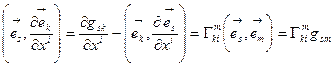(10.7)

Сложим равенства (10.6) и (10.7) и воспользуемся свойством (10.5):

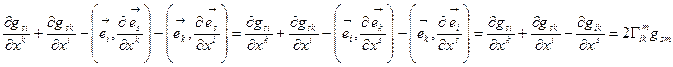
или окончательно 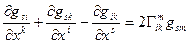(10.8)

ОПРЕДЕЛЕНИЕ 10.1. Символами Кристофелля первого рода называется множество функций вида: 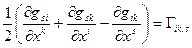(10.9)

Воспользовавшись этим определением, перепишем формулу (10.8)

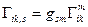(10.10)

Нетрудно сообразить, что формула (10.10) задает операцию опускания индекса, поэтому обратная операция будет иметь вид 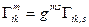. Следует напомнить еще раз о том, что символы Кристоффеля, как первого, так и второго родов, в общем случае не являются тензорами, несмотря на то, что для них справедливы тензорные операции.

Рассмотрим контравариантный базис. Построим производную от базисного вектора и разложим ее в собственном базисе. По аналогии с формулой (10.2) запишем:

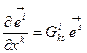(10.11)

Здесь коэффициенты разложения 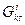играют такую же роль, что и символы Кристоффеля. Докажем, что 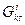с точностью до знака совпадают с 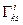. Для этого воспользуемся свойством 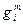и

продифференцируем его компоненты по .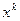

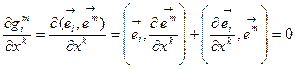
Подставим (10.2) и (10.11)

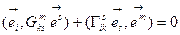
Преобразуем это выражения, выделяя соответствующие компоненты смешанного ФМТГ.

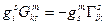
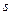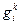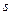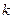Сумма по элементарно вычисляется (см. свойство ) тогда, переставляя индексы и у 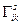, получим: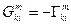

Таким образом, нет необходимости вводить коэффициенты разложения 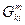т.к. производная от контравариантного базисного вектора в собственном базисе имеет вид:

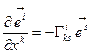(10.12)

Формулы (10.2) и (10.12) потребуются нам в дальнейшем, а здесь следует еще раз подчеркнуть - фундаментальный смысл символов Кристоффеля состоит в том, что с их помощью можно сравнивать компоненты вектора в двух бесконечно близких точках пространства. Так для произвольного вектора 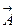дифференциал вычисляется следующим образом:

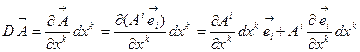(10.13)

Преобразуем это выражение, используя формулу (10.2) и меняя местами индексы суммирования 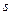и :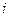

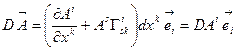(10.14)

Здесь - 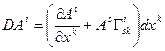- истинное приращение, 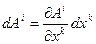- полное приращение,

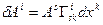- приращение компоненты вектора, связанное с выбором КСК и отражающее тот факт, что базис 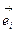является локальным.